Learning temporal formulas from examples is hard

We study the problem of learning linear temporal logic (LTL) formulas from examples, as a first step towards expressing a property separating positive and negative instances in a way that is comprehensible for humans. In this paper we initiate the study of the computational complexity of the problem. Our main results are hardness results: we show that the LTL learning problem is NP-complete, both for the full logic and for almost all of its fragments. This motivates the search for efficient heuristics, and highlights the complexity of expressing separating properties in concise natural language.

Scaling Neural Program Synthesis with Distribution-based Search

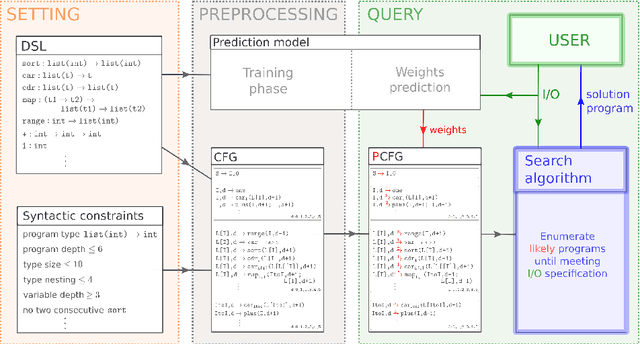
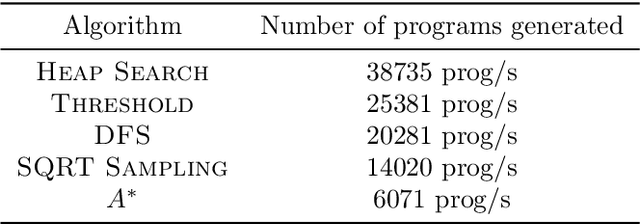
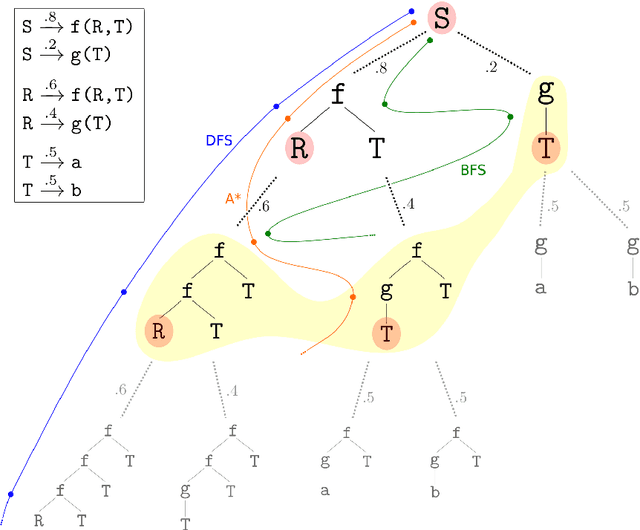
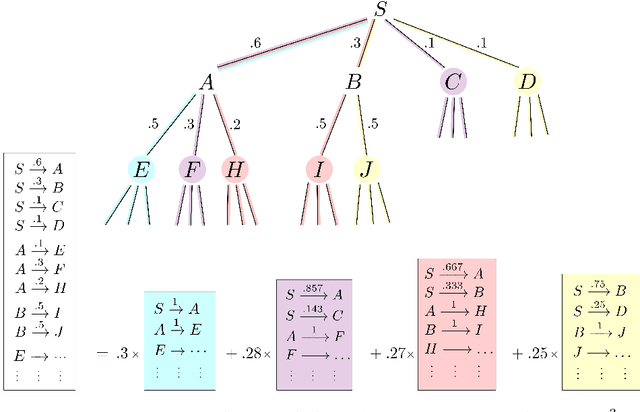
We consider the problem of automatically constructing computer programs from input-output examples. We investigate how to augment probabilistic and neural program synthesis methods with new search algorithms, proposing a framework called distribution-based search. Within this framework, we introduce two new search algorithms: Heap Search, an enumerative method, and SQRT Sampling, a probabilistic method. We prove certain optimality guarantees for both methods, show how they integrate with probabilistic and neural techniques, and demonstrate how they can operate at scale across parallel compute environments. Collectively these findings offer theoretical and applied studies of search algorithms for program synthesis that integrate with recent developments in machine-learned program synthesizers.

The Complexity of Learning Linear Temporal Formulas from Examples

In this paper we initiate the study of the computational complexity of learning linear temporal logic (LTL) formulas from examples. We construct approximation algorithms for fragments of LTL and prove hardness results; in particular we obtain tight bounds for approximation of the fragment containing only the next operator and conjunctions, and prove NP-completeness results for many fragments.

On Efficient Low Distortion Ultrametric Embedding

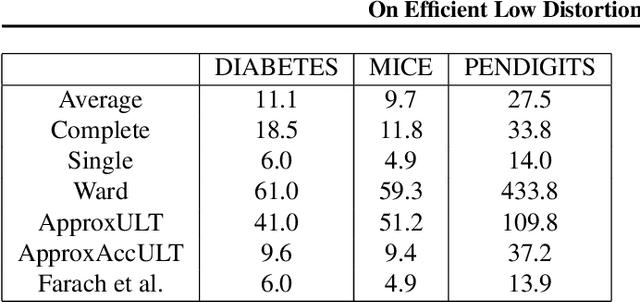
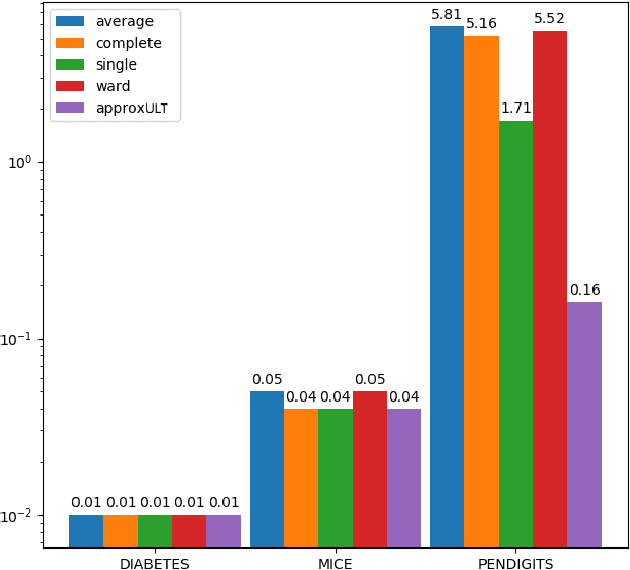
A classic problem in unsupervised learning and data analysis is to find simpler and easy-to-visualize representations of the data that preserve its essential properties. A widely-used method to preserve the underlying hierarchical structure of the data while reducing its complexity is to find an embedding of the data into a tree or an ultrametric. The most popular algorithms for this task are the classic linkage algorithms (single, average, or complete). However, these methods on a data set of $n$ points in $\Omega(\log n)$ dimensions exhibit a quite prohibitive running time of $\Theta(n^2)$. In this paper, we provide a new algorithm which takes as input a set of points $P$ in $\mathbb{R}^d$, and for every $c\ge 1$, runs in time $n^{1+\frac{\rho}{c^2}}$ (for some universal constant $\rho>1$) to output an ultrametric $\Delta$ such that for any two points $u,v$ in $P$, we have $\Delta(u,v)$ is within a multiplicative factor of $5c$ to the distance between $u$ and $v$ in the "best" ultrametric representation of $P$. Here, the best ultrametric is the ultrametric $\tilde\Delta$ that minimizes the maximum distance distortion with respect to the $\ell_2$ distance, namely that minimizes $\underset{u,v \in P}{\max}\ \frac{\tilde\Delta(u,v)}{\|u-v\|_2}$. We complement the above result by showing that under popular complexity theoretic assumptions, for every constant $\varepsilon>0$, no algorithm with running time $n^{2-\varepsilon}$ can distinguish between inputs in $\ell_\infty$-metric that admit isometric embedding and those that incur a distortion of $\frac{3}{2}$. Finally, we present empirical evaluation on classic machine learning datasets and show that the output of our algorithm is comparable to the output of the linkage algorithms while achieving a much faster running time.