Surya Teja Gavva
Impossibility of Depth Reduction in Explainable Clustering
May 04, 2023Abstract:Over the last few years Explainable Clustering has gathered a lot of attention. Dasgupta et al. [ICML'20] initiated the study of explainable k-means and k-median clustering problems where the explanation is captured by a threshold decision tree which partitions the space at each node using axis parallel hyperplanes. Recently, Laber et al. [Pattern Recognition'23] made a case to consider the depth of the decision tree as an additional complexity measure of interest. In this work, we prove that even when the input points are in the Euclidean plane, then any depth reduction in the explanation incurs unbounded loss in the k-means and k-median cost. Formally, we show that there exists a data set X in the Euclidean plane, for which there is a decision tree of depth k-1 whose k-means/k-median cost matches the optimal clustering cost of X, but every decision tree of depth less than k-1 has unbounded cost w.r.t. the optimal cost of clustering. We extend our results to the k-center objective as well, albeit with weaker guarantees.
Clustering Categorical Data: Soft Rounding k-modes
Oct 18, 2022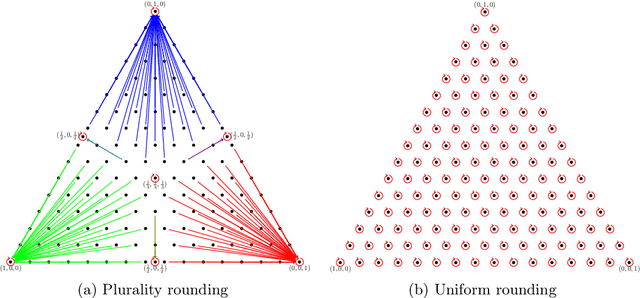
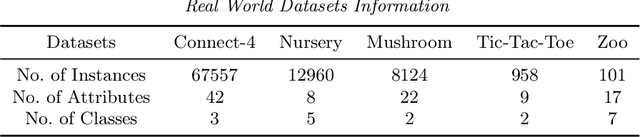
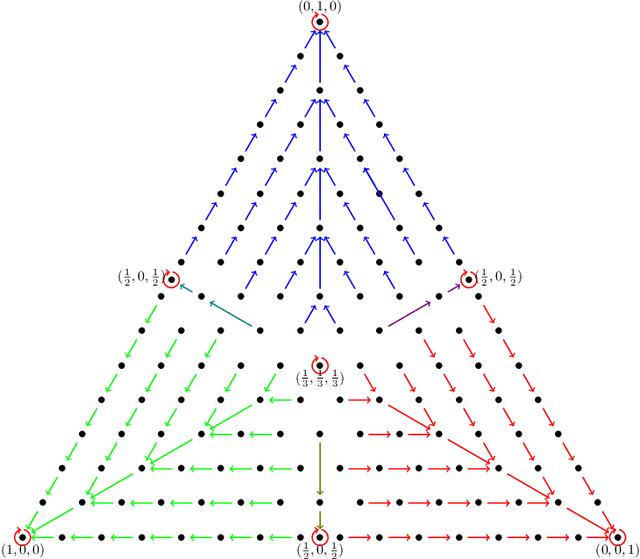
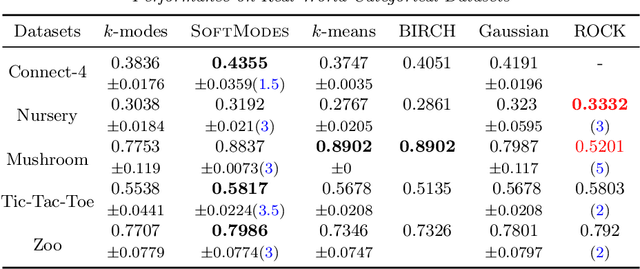
Abstract:Over the last three decades, researchers have intensively explored various clustering tools for categorical data analysis. Despite the proposal of various clustering algorithms, the classical k-modes algorithm remains a popular choice for unsupervised learning of categorical data. Surprisingly, our first insight is that in a natural generative block model, the k-modes algorithm performs poorly for a large range of parameters. We remedy this issue by proposing a soft rounding variant of the k-modes algorithm (SoftModes) and theoretically prove that our variant addresses the drawbacks of the k-modes algorithm in the generative model. Finally, we empirically verify that SoftModes performs well on both synthetic and real-world datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge