On Approximability of $\ell_2^2$ Min-Sum Clustering

The $\ell_2^2$ min-sum $k$-clustering problem is to partition an input set into clusters $C_1,\ldots,C_k$ to minimize $\sum_{i=1}^k\sum_{p,q\in C_i}\|p-q\|_2^2$. Although $\ell_2^2$ min-sum $k$-clustering is NP-hard, it is not known whether it is NP-hard to approximate $\ell_2^2$ min-sum $k$-clustering beyond a certain factor. In this paper, we give the first hardness-of-approximation result for the $\ell_2^2$ min-sum $k$-clustering problem. We show that it is NP-hard to approximate the objective to a factor better than $1.056$ and moreover, assuming a balanced variant of the Johnson Coverage Hypothesis, it is NP-hard to approximate the objective to a factor better than 1.327. We then complement our hardness result by giving the first $(1+\varepsilon)$-coreset construction for $\ell_2^2$ min-sum $k$-clustering. Our coreset uses $\mathcal{O}\left(k^{\varepsilon^{-4}}\right)$ space and can be leveraged to achieve a polynomial-time approximation scheme with runtime $nd\cdot f(k,\varepsilon^{-1})$, where $d$ is the underlying dimension of the input dataset and $f$ is a fixed function. Finally, we consider a learning-augmented setting, where the algorithm has access to an oracle that outputs a label $i\in[k]$ for input point, thereby implicitly partitioning the input dataset into $k$ clusters that induce an approximately optimal solution, up to some amount of adversarial error $\alpha\in\left[0,\frac{1}{2}\right)$. We give a polynomial-time algorithm that outputs a $\frac{1+\gamma\alpha}{(1-\alpha)^2}$-approximation to $\ell_2^2$ min-sum $k$-clustering, for a fixed constant $\gamma>0$.

Causal Discovery under Latent Class Confounding

Directed acyclic graphs are used to model the causal structure of a system. ``Causal discovery'' describes the problem of learning this structure from data. When data is an aggregate from multiple sources (populations or environments), global confounding obscures conditional independence properties that drive many causal discovery algorithms. For this reason, existing causal discovery algorithms are not suitable for the multiple-source setting. We demonstrate that, if the confounding is of bounded cardinality (i.e. the data comes from a limited number of sources), causal discovery can still be achieved. The feasibility of this problem is governed by a trade-off between the cardinality of the global confounder, the cardinalities of the observed variables, and the sparsity of the causal structure.

Identification of Mixtures of Discrete Product Distributions in Near-Optimal Sample and Time Complexity

We consider the problem of identifying, from statistics, a distribution of discrete random variables $X_1,\ldots,X_n$ that is a mixture of $k$ product distributions. The best previous sample complexity for $n \in O(k)$ was $(1/\zeta)^{O(k^2 \log k)}$ (under a mild separation assumption parameterized by $\zeta$). The best known lower bound was $\exp(\Omega(k))$. It is known that $n\geq 2k-1$ is necessary and sufficient for identification. We show, for any $n\geq 2k-1$, how to achieve sample complexity and run-time complexity $(1/\zeta)^{O(k)}$. We also extend the known lower bound of $e^{\Omega(k)}$ to match our upper bound across a broad range of $\zeta$. Our results are obtained by combining (a) a classic method for robust tensor decomposition, (b) a novel way of bounding the condition number of key matrices called Hadamard extensions, by studying their action only on flattened rank-1 tensors.

Identifying Mixtures of Bayesian Network Distributions

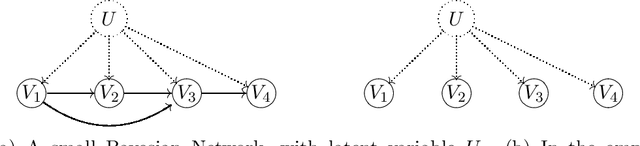
A Bayesian Network is a directed acyclic graph (DAG) on a set of $n$ random variables (identified with the vertices); a Bayesian Network Distribution (BND) is a probability distribution on the rv's that is Markovian on the graph. A finite mixture of such models is the projection on these variables of a BND on the larger graph which has an additional "hidden" (or "latent") random variable $U$, ranging in $\{1,\ldots,k\}$, and a directed edge from $U$ to every other vertex. Models of this type are fundamental to research in Causal Inference, where $U$ models a confounding effect. One extremely special case has been of longstanding interest in the theory literature: the empty graph. Such a distribution is simply a mixture of $k$ product distributions. A longstanding problem has been, given the joint distribution of a mixture of $k$ product distributions, to identify each of the product distributions, and their mixture weights. Our results are: (1) We improve the sample complexity (and runtime) for identifying mixtures of $k$ product distributions from $\exp(O(k^2))$ to $\exp(O(k \log k))$. This is almost best possible in view of a known $\exp(\Omega(k))$ lower bound. (2) We give the first algorithm for the case of non-empty graphs. The complexity for a graph of maximum degree $\Delta$ is $\exp(O(k(\Delta^2 + \log k)))$. (The above complexities are approximate and suppress dependence on secondary parameters.)

Source Identification for Mixtures of Product Distributions

We give an algorithm for source identification of a mixture of $k$ product distributions on $n$ bits. This is a fundamental problem in machine learning with many applications. Our algorithm identifies the source parameters of an identifiable mixture, given, as input, approximate values of multilinear moments (derived, for instance, from a sufficiently large sample), using $2^{O(k^2)} n^{O(k)}$ arithmetic operations. Our result is the first explicit bound on the computational complexity of source identification of such mixtures. The running time improves previous results by Feldman, O'Donnell, and Servedio (FOCS 2005) and Chen and Moitra (STOC 2019) that guaranteed only learning the mixture (without parametric identification of the source). Our analysis gives a quantitative version of a qualitative characterization of identifiable sources that is due to Tahmasebi, Motahari, and Maddah-Ali (ISIT 2018).

The Sparse Hausdorff Moment Problem, with Application to Topic Models

We consider the problem of identifying, from its first $m$ noisy moments, a probability distribution on $[0,1]$ of support $k<\infty$. This is equivalent to the problem of learning a distribution on $m$ observable binary random variables $X_1,X_2,\dots,X_m$ that are iid conditional on a hidden random variable $U$ taking values in $\{1,2,\dots,k\}$. Our focus is on accomplishing this with $m=2k$, which is the minimum $m$ for which verifying that the source is a $k$-mixture is possible (even with exact statistics). This problem, so simply stated, is quite useful: e.g., by a known reduction, any algorithm for it lifts to an algorithm for learning pure topic models. In past work on this and also the more general mixture-of-products problem ($X_i$ independent conditional on $U$, but not necessarily iid), a barrier at $m^{O(k^2)}$ on the sample complexity and/or runtime of the algorithm was reached. We improve this substantially. We show it suffices to use a sample of size $\exp(k\log k)$ (with $m=2k$). It is known that the sample complexity of any solution to the identification problem must be $\exp(\Omega(k))$. Stated in terms of the moment problem, it suffices to know the moments to additive accuracy $\exp(-k\log k)$. Our run-time for the moment problem is only $O(k^{2+o(1)})$ arithmetic operations.

Online Multiserver Convex Chasing and Optimization

We introduce the problem of $k$-chasing of convex functions, a simultaneous generalization of both the famous k-server problem in $R^d$, and of the problem of chasing convex bodies and functions. Aside from fundamental interest in this general form, it has natural applications to online $k$-clustering problems with objectives such as $k$-median or $k$-means. We show that this problem exhibits a rich landscape of behavior. In general, if both $k > 1$ and $d > 1$ there does not exist any online algorithm with bounded competitiveness. By contrast, we exhibit a class of nicely behaved functions (which include in particular the above-mentioned clustering problems), for which we show that competitive online algorithms exist, and moreover with dimension-free competitive ratio. We also introduce a parallel question of top-$k$ action regret minimization in the realm of online convex optimization. There, too, a much rougher landscape emerges for $k > 1$. While it is possible to achieve vanishing regret, unlike the top-one action case the rate of vanishing does not speed up for strongly convex functions. Moreover, vanishing regret necessitates both intractable computations and randomness. Finally we leave open whether almost dimension-free regret is achievable for $k > 1$ and general convex losses. As evidence that it might be possible, we prove dimension-free regret for linear losses via an information-theoretic argument.

Learning Arbitrary Statistical Mixtures of Discrete Distributions

We study the problem of learning from unlabeled samples very general statistical mixture models on large finite sets. Specifically, the model to be learned, $\vartheta$, is a probability distribution over probability distributions $p$, where each such $p$ is a probability distribution over $[n] = \{1,2,\dots,n\}$. When we sample from $\vartheta$, we do not observe $p$ directly, but only indirectly and in very noisy fashion, by sampling from $[n]$ repeatedly, independently $K$ times from the distribution $p$. The problem is to infer $\vartheta$ to high accuracy in transportation (earthmover) distance. We give the first efficient algorithms for learning this mixture model without making any restricting assumptions on the structure of the distribution $\vartheta$. We bound the quality of the solution as a function of the size of the samples $K$ and the number of samples used. Our model and results have applications to a variety of unsupervised learning scenarios, including learning topic models and collaborative filtering.

Learning Mixtures of Arbitrary Distributions over Large Discrete Domains

We give an algorithm for learning a mixture of {\em unstructured} distributions. This problem arises in various unsupervised learning scenarios, for example in learning {\em topic models} from a corpus of documents spanning several topics. We show how to learn the constituents of a mixture of $k$ arbitrary distributions over a large discrete domain $[n]=\{1,2,\dots,n\}$ and the mixture weights, using $O(n\polylog n)$ samples. (In the topic-model learning setting, the mixture constituents correspond to the topic distributions.) This task is information-theoretically impossible for $k>1$ under the usual sampling process from a mixture distribution. However, there are situations (such as the above-mentioned topic model case) in which each sample point consists of several observations from the same mixture constituent. This number of observations, which we call the {\em "sampling aperture"}, is a crucial parameter of the problem. We obtain the {\em first} bounds for this mixture-learning problem {\em without imposing any assumptions on the mixture constituents.} We show that efficient learning is possible exactly at the information-theoretically least-possible aperture of $2k-1$. Thus, we achieve near-optimal dependence on $n$ and optimal aperture. While the sample-size required by our algorithm depends exponentially on $k$, we prove that such a dependence is {\em unavoidable} when one considers general mixtures. A sequence of tools contribute to the algorithm, such as concentration results for random matrices, dimension reduction, moment estimations, and sensitivity analysis.