Identifying Mixtures of Bayesian Network Distributions
Paper and Code
Dec 22, 2021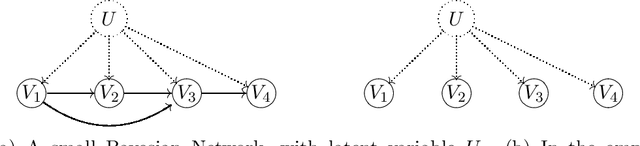

A Bayesian Network is a directed acyclic graph (DAG) on a set of $n$ random variables (identified with the vertices); a Bayesian Network Distribution (BND) is a probability distribution on the rv's that is Markovian on the graph. A finite mixture of such models is the projection on these variables of a BND on the larger graph which has an additional "hidden" (or "latent") random variable $U$, ranging in $\{1,\ldots,k\}$, and a directed edge from $U$ to every other vertex. Models of this type are fundamental to research in Causal Inference, where $U$ models a confounding effect. One extremely special case has been of longstanding interest in the theory literature: the empty graph. Such a distribution is simply a mixture of $k$ product distributions. A longstanding problem has been, given the joint distribution of a mixture of $k$ product distributions, to identify each of the product distributions, and their mixture weights. Our results are: (1) We improve the sample complexity (and runtime) for identifying mixtures of $k$ product distributions from $\exp(O(k^2))$ to $\exp(O(k \log k))$. This is almost best possible in view of a known $\exp(\Omega(k))$ lower bound. (2) We give the first algorithm for the case of non-empty graphs. The complexity for a graph of maximum degree $\Delta$ is $\exp(O(k(\Delta^2 + \log k)))$. (The above complexities are approximate and suppress dependence on secondary parameters.)
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge