Identifiability of Product of Experts Models

Product of experts (PoE) are layered networks in which the value at each node is an AND (or product) of the values (possibly negated) at its inputs. These were introduced as a neural network architecture that can efficiently learn to generate high-dimensional data which satisfy many low-dimensional constraints -- thereby allowing each individual expert to perform a simple task. PoEs have found a variety of applications in learning. We study the problem of identifiability of a product of experts model having a layer of binary latent variables, and a layer of binary observables that are iid conditional on the latents. The previous best upper bound on the number of observables needed to identify the model was exponential in the number of parameters. We show: (a) When the latents are uniformly distributed, the model is identifiable with a number of observables equal to the number of parameters (and hence best possible). (b) In the more general case of arbitrarily distributed latents, the model is identifiable for a number of observables that is still linear in the number of parameters (and within a factor of two of best-possible). The proofs rely on root interlacing phenomena for some special three-term recurrences.

Identification of Mixtures of Discrete Product Distributions in Near-Optimal Sample and Time Complexity

We consider the problem of identifying, from statistics, a distribution of discrete random variables $X_1,\ldots,X_n$ that is a mixture of $k$ product distributions. The best previous sample complexity for $n \in O(k)$ was $(1/\zeta)^{O(k^2 \log k)}$ (under a mild separation assumption parameterized by $\zeta$). The best known lower bound was $\exp(\Omega(k))$. It is known that $n\geq 2k-1$ is necessary and sufficient for identification. We show, for any $n\geq 2k-1$, how to achieve sample complexity and run-time complexity $(1/\zeta)^{O(k)}$. We also extend the known lower bound of $e^{\Omega(k)}$ to match our upper bound across a broad range of $\zeta$. Our results are obtained by combining (a) a classic method for robust tensor decomposition, (b) a novel way of bounding the condition number of key matrices called Hadamard extensions, by studying their action only on flattened rank-1 tensors.

Identifying Mixtures of Bayesian Network Distributions

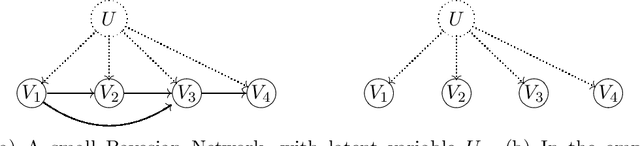
A Bayesian Network is a directed acyclic graph (DAG) on a set of $n$ random variables (identified with the vertices); a Bayesian Network Distribution (BND) is a probability distribution on the rv's that is Markovian on the graph. A finite mixture of such models is the projection on these variables of a BND on the larger graph which has an additional "hidden" (or "latent") random variable $U$, ranging in $\{1,\ldots,k\}$, and a directed edge from $U$ to every other vertex. Models of this type are fundamental to research in Causal Inference, where $U$ models a confounding effect. One extremely special case has been of longstanding interest in the theory literature: the empty graph. Such a distribution is simply a mixture of $k$ product distributions. A longstanding problem has been, given the joint distribution of a mixture of $k$ product distributions, to identify each of the product distributions, and their mixture weights. Our results are: (1) We improve the sample complexity (and runtime) for identifying mixtures of $k$ product distributions from $\exp(O(k^2))$ to $\exp(O(k \log k))$. This is almost best possible in view of a known $\exp(\Omega(k))$ lower bound. (2) We give the first algorithm for the case of non-empty graphs. The complexity for a graph of maximum degree $\Delta$ is $\exp(O(k(\Delta^2 + \log k)))$. (The above complexities are approximate and suppress dependence on secondary parameters.)

Hadamard Extensions and the Identification of Mixtures of Product Distributions

The Hadamard Extension of a matrix is the matrix consisting of all Hadamard products of subsets of its rows. This construction arises in the context of identifying a mixture of product distributions on binary random variables: full column rank of such extensions is a necessary ingredient of identification algorithms. We provide several results concerning when a Hadamard Extension has full column rank.

Source Identification for Mixtures of Product Distributions

We give an algorithm for source identification of a mixture of $k$ product distributions on $n$ bits. This is a fundamental problem in machine learning with many applications. Our algorithm identifies the source parameters of an identifiable mixture, given, as input, approximate values of multilinear moments (derived, for instance, from a sufficiently large sample), using $2^{O(k^2)} n^{O(k)}$ arithmetic operations. Our result is the first explicit bound on the computational complexity of source identification of such mixtures. The running time improves previous results by Feldman, O'Donnell, and Servedio (FOCS 2005) and Chen and Moitra (STOC 2019) that guaranteed only learning the mixture (without parametric identification of the source). Our analysis gives a quantitative version of a qualitative characterization of identifiable sources that is due to Tahmasebi, Motahari, and Maddah-Ali (ISIT 2018).

The Sparse Hausdorff Moment Problem, with Application to Topic Models

We consider the problem of identifying, from its first $m$ noisy moments, a probability distribution on $[0,1]$ of support $k<\infty$. This is equivalent to the problem of learning a distribution on $m$ observable binary random variables $X_1,X_2,\dots,X_m$ that are iid conditional on a hidden random variable $U$ taking values in $\{1,2,\dots,k\}$. Our focus is on accomplishing this with $m=2k$, which is the minimum $m$ for which verifying that the source is a $k$-mixture is possible (even with exact statistics). This problem, so simply stated, is quite useful: e.g., by a known reduction, any algorithm for it lifts to an algorithm for learning pure topic models. In past work on this and also the more general mixture-of-products problem ($X_i$ independent conditional on $U$, but not necessarily iid), a barrier at $m^{O(k^2)}$ on the sample complexity and/or runtime of the algorithm was reached. We improve this substantially. We show it suffices to use a sample of size $\exp(k\log k)$ (with $m=2k$). It is known that the sample complexity of any solution to the identification problem must be $\exp(\Omega(k))$. Stated in terms of the moment problem, it suffices to know the moments to additive accuracy $\exp(-k\log k)$. Our run-time for the moment problem is only $O(k^{2+o(1)})$ arithmetic operations.

Learning Arbitrary Statistical Mixtures of Discrete Distributions

We study the problem of learning from unlabeled samples very general statistical mixture models on large finite sets. Specifically, the model to be learned, $\vartheta$, is a probability distribution over probability distributions $p$, where each such $p$ is a probability distribution over $[n] = \{1,2,\dots,n\}$. When we sample from $\vartheta$, we do not observe $p$ directly, but only indirectly and in very noisy fashion, by sampling from $[n]$ repeatedly, independently $K$ times from the distribution $p$. The problem is to infer $\vartheta$ to high accuracy in transportation (earthmover) distance. We give the first efficient algorithms for learning this mixture model without making any restricting assumptions on the structure of the distribution $\vartheta$. We bound the quality of the solution as a function of the size of the samples $K$ and the number of samples used. Our model and results have applications to a variety of unsupervised learning scenarios, including learning topic models and collaborative filtering.