Transformers Struggle to Learn to Search

Search is an ability foundational in many important tasks, and recent studies have shown that large language models (LLMs) struggle to perform search robustly. It is unknown whether this inability is due to a lack of data, insufficient model parameters, or fundamental limitations of the transformer architecture. In this work, we use the foundational graph connectivity problem as a testbed to generate effectively limitless high-coverage data to train small transformers and test whether they can learn to perform search. We find that, when given the right training distribution, the transformer is able to learn to search. We analyze the algorithm that the transformer has learned through a novel mechanistic interpretability technique that enables us to extract the computation graph from the trained model. We find that for each vertex in the input graph, transformers compute the set of vertices reachable from that vertex. Each layer then progressively expands these sets, allowing the model to search over a number of vertices exponential in the number of layers. However, we find that as the input graph size increases, the transformer has greater difficulty in learning the task. This difficulty is not resolved even as the number of parameters is increased, suggesting that increasing model scale will not lead to robust search abilities. We also find that performing search in-context (i.e., chain-of-thought) does not resolve this inability to learn to search on larger graphs.

Testing the General Deductive Reasoning Capacity of Large Language Models Using OOD Examples

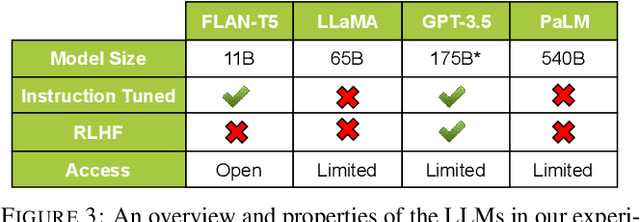
Given the intractably large size of the space of proofs, any model that is capable of general deductive reasoning must generalize to proofs of greater complexity. Recent studies have shown that large language models (LLMs) possess some abstract deductive reasoning ability given chain-of-thought prompts. However, they have primarily been tested on proofs using modus ponens or of a specific size, and from the same distribution as the in-context examples. To measure the general deductive reasoning ability of LLMs, we test on a broad set of deduction rules and measure their ability to generalize to more complex proofs from simpler demonstrations from multiple angles: depth-, width-, and compositional generalization. To facilitate systematic exploration, we construct a new synthetic and programmable reasoning dataset that enables control over deduction rules and proof complexity. Our experiments on four LLMs of various sizes and training objectives show that they are able to generalize to longer and compositional proofs. However, they require explicit demonstrations to produce hypothetical subproofs, specifically in proof by cases and proof by contradiction.

LAMBADA: Backward Chaining for Automated Reasoning in Natural Language

Remarkable progress has been made on automated reasoning with knowledge specified as unstructured, natural text, by using the power of large language models (LMs) coupled with methods such as Chain-of-Thought prompting and Selection-Inference. These techniques search for proofs in the forward direction from axioms to the conclusion, which suffers from a combinatorial explosion of the search space, and thus high failure rates for problems requiring longer chains of reasoning. The classical automated reasoning literature has shown that reasoning in the backward direction (i.e. from the intended conclusion to the set of axioms that support it) is significantly more efficient at proof-finding problems. We import this intuition into the LM setting and develop a Backward Chaining algorithm, which we call LAMBADA, that decomposes reasoning into four sub-modules, each of which can be simply implemented by few-shot prompted LM inference. We show that LAMBADA achieves massive accuracy boosts over state-of-the-art forward reasoning methods on two challenging logical reasoning datasets, particularly when deep and accurate proof chains are required.

TwiRGCN: Temporally Weighted Graph Convolution for Question Answering over Temporal Knowledge Graphs

Recent years have witnessed much interest in temporal reasoning over knowledge graphs (KG) for complex question answering (QA), but there remains a substantial gap in human capabilities. We explore how to generalize relational graph convolutional networks (RGCN) for temporal KGQA. Specifically, we propose a novel, intuitive and interpretable scheme to modulate the messages passed through a KG edge during convolution, based on the relevance of its associated time period to the question. We also introduce a gating device to predict if the answer to a complex temporal question is likely to be a KG entity or time and use this prediction to guide our scoring mechanism. We evaluate the resulting system, which we call TwiRGCN, on TimeQuestions, a recently released, challenging dataset for multi-hop complex temporal QA. We show that TwiRGCN significantly outperforms state-of-the-art systems on this dataset across diverse question types. Notably, TwiRGCN improves accuracy by 9--10 percentage points for the most difficult ordinal and implicit question types.

Tackling Provably Hard Representative Selection via Graph Neural Networks

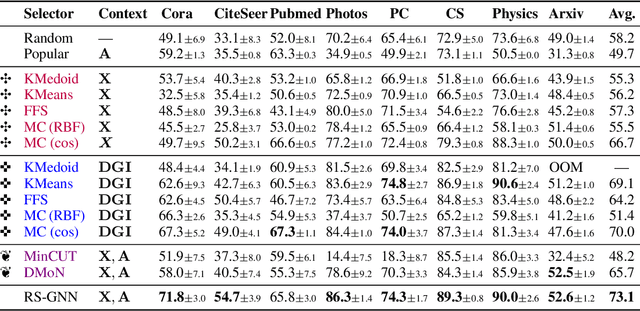
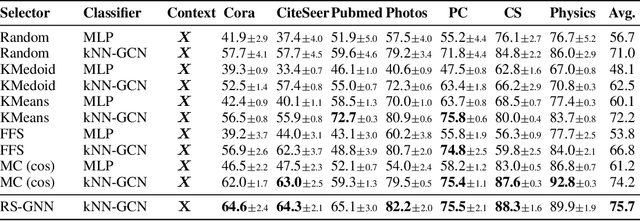
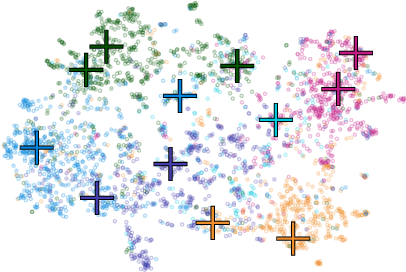
Representative selection (RS) is the problem of finding a small subset of exemplars from an unlabeled dataset, and has numerous applications in summarization, active learning, data compression and many other domains. In this paper, we focus on finding representatives that optimize the accuracy of a model trained on the selected representatives. We study RS for data represented as attributed graphs. We develop RS-GNN, a representation learning-based RS model based on Graph Neural Networks. Empirically, we demonstrate the effectiveness of RS-GNN on problems with predefined graph structures as well as problems with graphs induced from node feature similarities, by showing that RS-GNN achieves significant improvements over established baselines that optimize surrogate functions. Theoretically, we establish a new hardness result for RS by proving that RS is hard to approximate in polynomial time within any reasonable factor, which implies a significant gap between the optimum solution of widely-used surrogate functions and the actual accuracy of the model, and provides justification for the superiority of representation learning-based approaches such as RS-GNN over surrogate functions.

SLAPS: Self-Supervision Improves Structure Learning for Graph Neural Networks

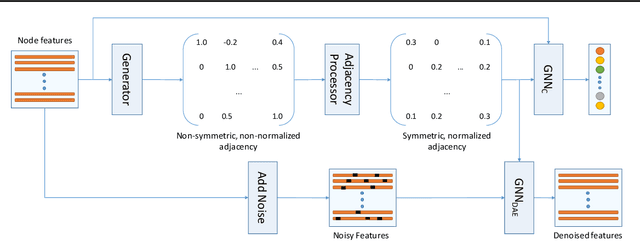
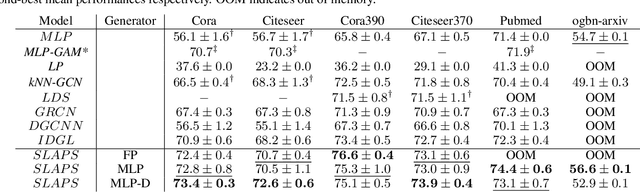
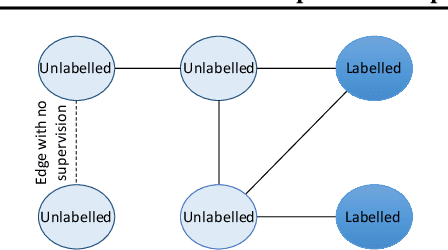
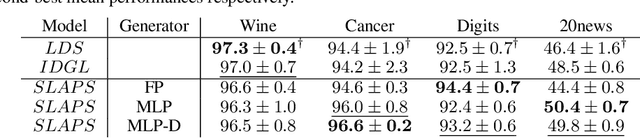
Graph neural networks (GNNs) work well when the graph structure is provided. However, this structure may not always be available in real-world applications. One solution to this problem is to infer a task-specific latent structure and then apply a GNN to the inferred graph. Unfortunately, the space of possible graph structures grows super-exponentially with the number of nodes and so the task-specific supervision may be insufficient for learning both the structure and the GNN parameters. In this work, we propose the Simultaneous Learning of Adjacency and GNN Parameters with Self-supervision, or SLAPS, a method that provides more supervision for inferring a graph structure through self-supervision. A comprehensive experimental study demonstrates that SLAPS scales to large graphs with hundreds of thousands of nodes and outperforms several models that have been proposed to learn a task-specific graph structure on established benchmarks.

Out-of-Sample Representation Learning for Multi-Relational Graphs

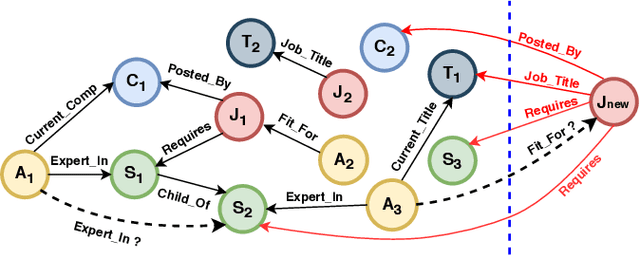
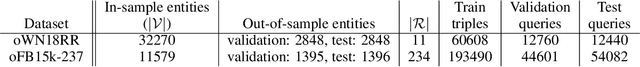
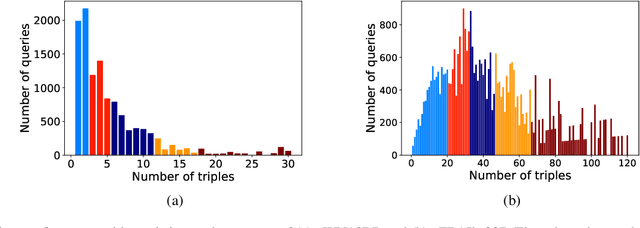
Many important problems can be formulated as reasoning in multi-relational graphs. Representation learning has proved extremely effective for transductive reasoning, in which one needs to make new predictions for already observed entities. This is true for both attributed graphs (where each entity has an initial feature vector) and non-attributed graphs(where the only initial information derives from known relations with other entities). For out-of-sample reasoning, where one needs to make predictions for entities that were unseen at training time, much prior work considers attributed graph. However, this problem has been surprisingly left unexplored for non-attributed graphs. In this paper, we introduce the out-of-sample representation learning problem for non-attributed multi-relational graphs, create benchmark datasets for this task, develop several models and baselines, and provide empirical analyses and comparisons of the proposed models and baselines.

Time2Vec: Learning a Vector Representation of Time

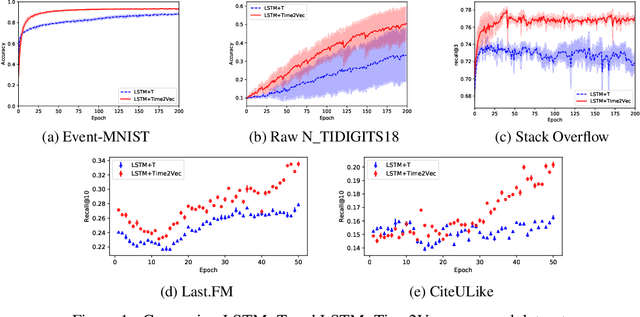
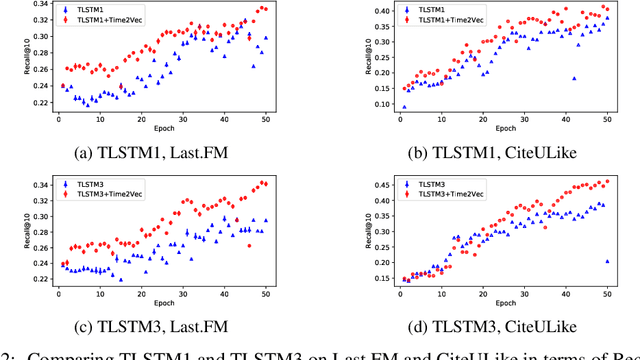
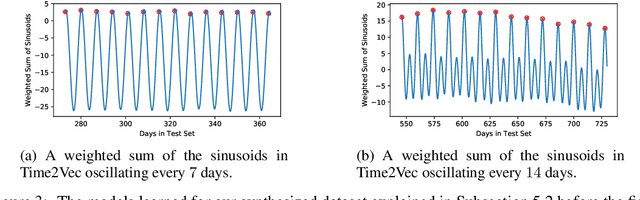
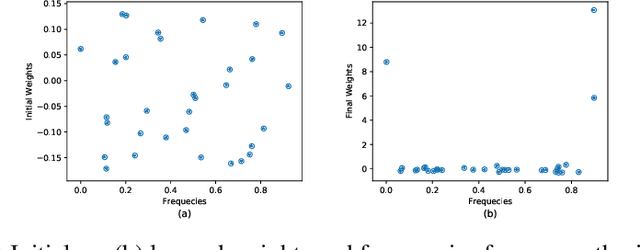
Time is an important feature in many applications involving events that occur synchronously and/or asynchronously. To effectively consume time information, recent studies have focused on designing new architectures. In this paper, we take an orthogonal but complementary approach by providing a model-agnostic vector representation for time, called Time2Vec, that can be easily imported into many existing and future architectures and improve their performances. We show on a range of models and problems that replacing the notion of time with its Time2Vec representation improves the performance of the final model.

Diachronic Embedding for Temporal Knowledge Graph Completion

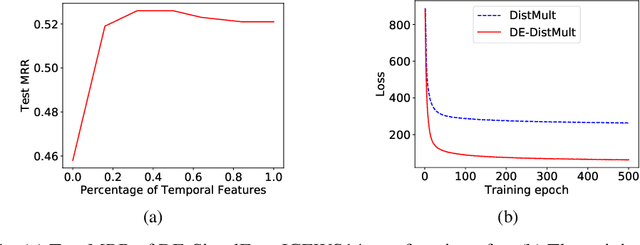
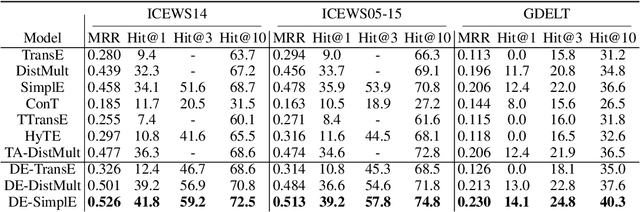
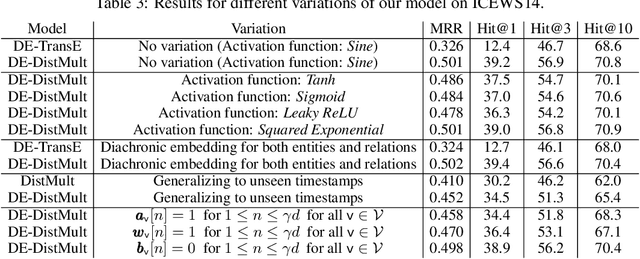
Knowledge graphs (KGs) typically contain temporal facts indicating relationships among entities at different times. Due to their incompleteness, several approaches have been proposed to infer new facts for a KG based on the existing ones-a problem known as KG completion. KG embedding approaches have proved effective for KG completion, however, they have been developed mostly for static KGs. Developing temporal KG embedding models is an increasingly important problem. In this paper, we build novel models for temporal KG completion through equipping static models with a diachronic entity embedding function which provides the characteristics of entities at any point in time. This is in contrast to the existing temporal KG embedding approaches where only static entity features are provided. The proposed embedding function is model-agnostic and can be potentially combined with any static model. We prove that combining it with SimplE, a recent model for static KG embedding, results in a fully expressive model for temporal KG completion. Our experiments indicate the superiority of our proposal compared to existing baselines.

Relational Representation Learning for Dynamic (Knowledge) Graphs: A Survey

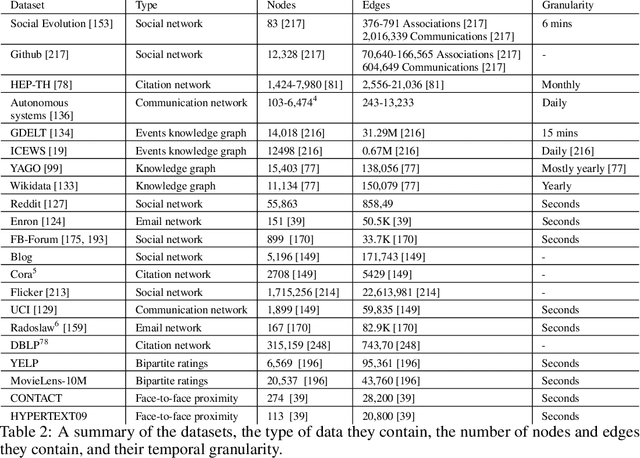
Graphs arise naturally in many real-world applications including social networks, recommender systems, ontologies, biology, and computational finance. Traditionally, machine learning models for graphs have been mostly designed for static graphs. However, many applications involve evolving graphs. This introduces important challenges for learning and inference since nodes, attributes, and edges change over time. In this survey, we review the recent advances in representation learning for dynamic graphs, including dynamic knowledge graphs. We describe existing models from an encoder-decoder perspective, categorize these encoders and decoders based on the techniques they employ, and analyze the approaches in each category. We also review several prominent applications and widely used datasets, and highlight directions for future research.