Abulhair Saparov
Reasoning Models Reason Well, Until They Don't
Oct 25, 2025Abstract:Large language models (LLMs) have shown significant progress in reasoning tasks. However, recent studies show that transformers and LLMs fail catastrophically once reasoning problems exceed modest complexity. We revisit these findings through the lens of large reasoning models (LRMs) -- LLMs fine-tuned with incentives for step-by-step argumentation and self-verification. LRM performance on graph and reasoning benchmarks such as NLGraph seem extraordinary, with some even claiming they are capable of generalized reasoning and innovation in reasoning-intensive fields such as mathematics, physics, medicine, and law. However, by more carefully scaling the complexity of reasoning problems, we show existing benchmarks actually have limited complexity. We develop a new dataset, the Deep Reasoning Dataset (DeepRD), along with a generative process for producing unlimited examples of scalable complexity. We use this dataset to evaluate model performance on graph connectivity and natural language proof planning. We find that the performance of LRMs drop abruptly at sufficient complexity and do not generalize. We also relate our LRM results to the distributions of the complexities of large, real-world knowledge graphs, interaction graphs, and proof datasets. We find the majority of real-world examples fall inside the LRMs' success regime, yet the long tails expose substantial failure potential. Our analysis highlights the near-term utility of LRMs while underscoring the need for new methods that generalize beyond the complexity of examples in the training distribution.
Transformers Can Learn Connectivity in Some Graphs but Not Others
Sep 26, 2025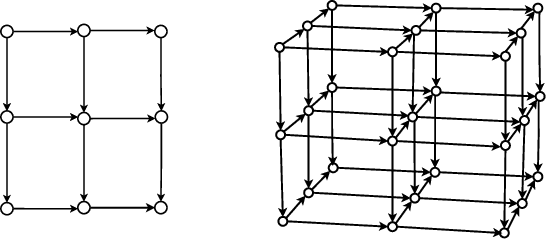
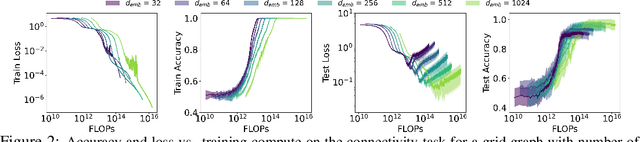
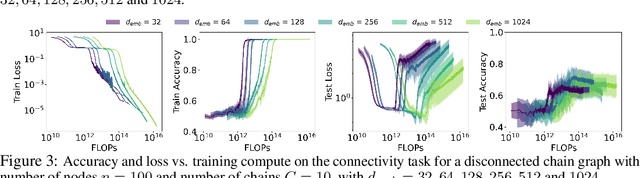
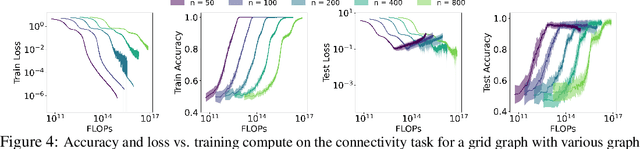
Abstract:Reasoning capability is essential to ensure the factual correctness of the responses of transformer-based Large Language Models (LLMs), and robust reasoning about transitive relations is instrumental in many settings, such as causal inference. Hence, it is essential to investigate the capability of transformers in the task of inferring transitive relations (e.g., knowing A causes B and B causes C, then A causes C). The task of inferring transitive relations is equivalent to the task of connectivity in directed graphs (e.g., knowing there is a path from A to B, and there is a path from B to C, then there is a path from A to C). Past research focused on whether transformers can learn to infer transitivity from in-context examples provided in the input prompt. However, transformers' capability to infer transitive relations from training examples and how scaling affects the ability is unexplored. In this study, we seek to answer this question by generating directed graphs to train transformer models of varying sizes and evaluate their ability to infer transitive relations for various graph sizes. Our findings suggest that transformers are capable of learning connectivity on "grid-like'' directed graphs where each node can be embedded in a low-dimensional subspace, and connectivity is easily inferable from the embeddings of the nodes. We find that the dimensionality of the underlying grid graph is a strong predictor of transformers' ability to learn the connectivity task, where higher-dimensional grid graphs pose a greater challenge than low-dimensional grid graphs. In addition, we observe that increasing the model scale leads to increasingly better generalization to infer connectivity over grid graphs. However, if the graph is not a grid graph and contains many disconnected components, transformers struggle to learn the connectivity task, especially when the number of components is large.
Language Models Do Not Follow Occam's Razor: A Benchmark for Inductive and Abductive Reasoning
Sep 03, 2025Abstract:Reasoning is a core capability in artificial intelligence systems, for which large language models (LLMs) have recently shown remarkable progress. However, most work focuses exclusively on deductive reasoning, which is problematic since other types of reasoning are also essential in solving real-world problems, and they are less explored. This work focuses on evaluating LLMs' inductive and abductive reasoning capabilities. We introduce a programmable and synthetic dataset, InAbHyD (pronounced in-a-bid), where each reasoning example consists of an incomplete world model and a set of observations. The task for the intelligent agent is to produce hypotheses to explain observations under the incomplete world model to solve each reasoning example. We propose a new metric to evaluate the quality of hypotheses based on Occam's Razor. We evaluate and analyze some state-of-the-art LLMs. Our analysis shows that LLMs can perform inductive and abductive reasoning in simple scenarios, but struggle with complex world models and producing high-quality hypotheses, even with popular reasoning-enhancing techniques such as in-context learning and RLVR.
Language Models Might Not Understand You: Evaluating Theory of Mind via Story Prompting
Jun 23, 2025Abstract:We introduce $\texttt{StorySim}$, a programmable framework for synthetically generating stories to evaluate the theory of mind (ToM) and world modeling (WM) capabilities of large language models (LLMs). Unlike prior benchmarks that may suffer from contamination in pretraining data, $\texttt{StorySim}$ produces novel, compositional story prompts anchored by a highly controllable $\texttt{Storyboard}$, enabling precise manipulation of character perspectives and events. We use this framework to design first- and second-order ToM tasks alongside WM tasks that control for the ability to track and model mental states. Our experiments across a suite of state-of-the-art LLMs reveal that most models perform better on WM tasks than ToM tasks, and that models tend to perform better reasoning with humans compared to inanimate objects. Additionally, our framework enabled us to find evidence of heuristic behavior such as recency bias and an over-reliance on earlier events in the story. All code for generating data and evaluations is freely available.
Revisiting Reinforcement Learning for LLM Reasoning from A Cross-Domain Perspective
Jun 17, 2025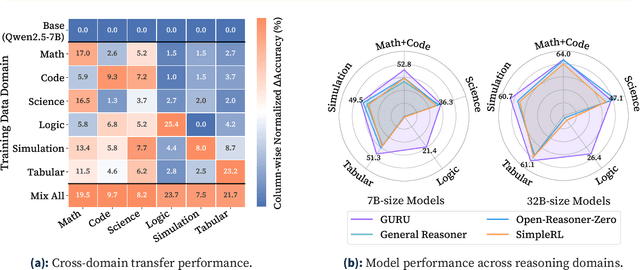
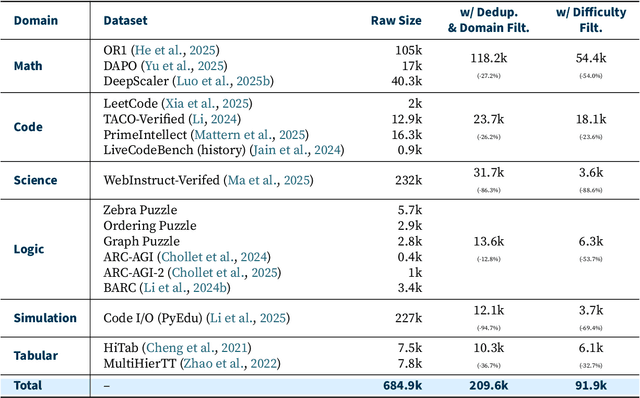
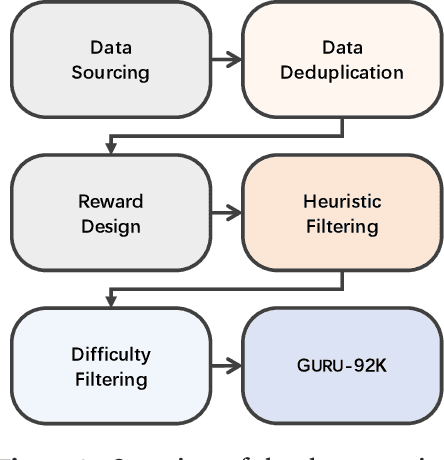

Abstract:Reinforcement learning (RL) has emerged as a promising approach to improve large language model (LLM) reasoning, yet most open efforts focus narrowly on math and code, limiting our understanding of its broader applicability to general reasoning. A key challenge lies in the lack of reliable, scalable RL reward signals across diverse reasoning domains. We introduce Guru, a curated RL reasoning corpus of 92K verifiable examples spanning six reasoning domains--Math, Code, Science, Logic, Simulation, and Tabular--each built through domain-specific reward design, deduplication, and filtering to ensure reliability and effectiveness for RL training. Based on Guru, we systematically revisit established findings in RL for LLM reasoning and observe significant variation across domains. For example, while prior work suggests that RL primarily elicits existing knowledge from pretrained models, our results reveal a more nuanced pattern: domains frequently seen during pretraining (Math, Code, Science) easily benefit from cross-domain RL training, while domains with limited pretraining exposure (Logic, Simulation, and Tabular) require in-domain training to achieve meaningful performance gains, suggesting that RL is likely to facilitate genuine skill acquisition. Finally, we present Guru-7B and Guru-32B, two models that achieve state-of-the-art performance among open models RL-trained with publicly available data, outperforming best baselines by 7.9% and 6.7% on our 17-task evaluation suite across six reasoning domains. We also show that our models effectively improve the Pass@k performance of their base models, particularly on complex tasks less likely to appear in pretraining data. We release data, models, training and evaluation code to facilitate general-purpose reasoning at: https://github.com/LLM360/Reasoning360
Transformers Struggle to Learn to Search
Dec 06, 2024



Abstract:Search is an ability foundational in many important tasks, and recent studies have shown that large language models (LLMs) struggle to perform search robustly. It is unknown whether this inability is due to a lack of data, insufficient model parameters, or fundamental limitations of the transformer architecture. In this work, we use the foundational graph connectivity problem as a testbed to generate effectively limitless high-coverage data to train small transformers and test whether they can learn to perform search. We find that, when given the right training distribution, the transformer is able to learn to search. We analyze the algorithm that the transformer has learned through a novel mechanistic interpretability technique that enables us to extract the computation graph from the trained model. We find that for each vertex in the input graph, transformers compute the set of vertices reachable from that vertex. Each layer then progressively expands these sets, allowing the model to search over a number of vertices exponential in the number of layers. However, we find that as the input graph size increases, the transformer has greater difficulty in learning the task. This difficulty is not resolved even as the number of parameters is increased, suggesting that increasing model scale will not lead to robust search abilities. We also find that performing search in-context (i.e., chain-of-thought) does not resolve this inability to learn to search on larger graphs.
MathGAP: Out-of-Distribution Evaluation on Problems with Arbitrarily Complex Proofs
Oct 17, 2024


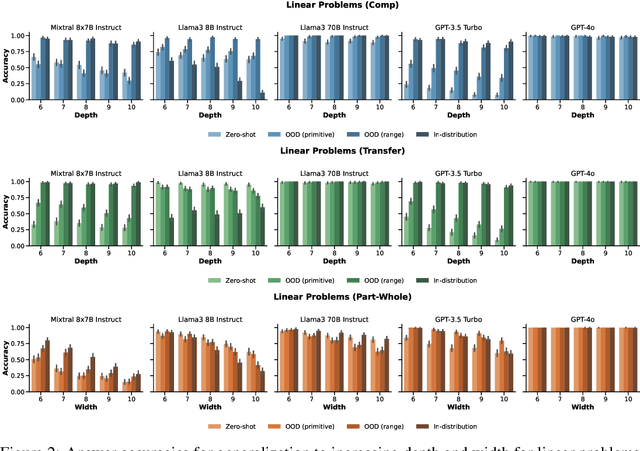
Abstract:Large language models (LLMs) can solve arithmetic word problems with high accuracy, but little is known about how well they generalize to problems that are more complex than the ones on which they have been trained. Empirical investigations of such questions are impeded by two major flaws of current evaluations: (i) much of the evaluation data is contaminated, in the sense that it has already been seen during training, and (ii) benchmark datasets do not capture how problem proofs may be arbitrarily complex in various ways. As a step towards addressing these issues, we present a framework for evaluating LLMs on problems that have arbitrarily complex arithmetic proofs, called MathGAP. MathGAP generates problems that follow fixed proof specifications -- along with chain-of-thought reasoning annotations -- enabling systematic studies on generalization with respect to arithmetic proof complexity. We apply MathGAP to analyze how in-context learning interacts with generalization to problems that have more complex proofs. We find that among the models tested, most show a significant decrease in performance as proofs get deeper and wider. This effect is more pronounced in complex, nonlinear proof structures, which are challenging even for GPT-4o. Surprisingly, providing in-context examples from the same distribution as the test set is not always beneficial for performance. In particular, zero-shot prompting as well as demonstrating a diverse range of examples that are less complex than the test data sometimes yield similar or higher accuracies.
A Practical Review of Mechanistic Interpretability for Transformer-Based Language Models
Jul 02, 2024



Abstract:Mechanistic interpretability (MI) is an emerging sub-field of interpretability that seeks to understand a neural network model by reverse-engineering its internal computations. Recently, MI has garnered significant attention for interpreting transformer-based language models (LMs), resulting in many novel insights yet introducing new challenges. However, there has not been work that comprehensively reviews these insights and challenges, particularly as a guide for newcomers to this field. To fill this gap, we present a comprehensive survey outlining fundamental objects of study in MI, techniques that have been used for its investigation, approaches for evaluating MI results, and significant findings and applications stemming from the use of MI to understand LMs. In particular, we present a roadmap for beginners to navigate the field and leverage MI for their benefit. Finally, we also identify current gaps in the field and discuss potential future directions.
LLMs Are Prone to Fallacies in Causal Inference
Jun 18, 2024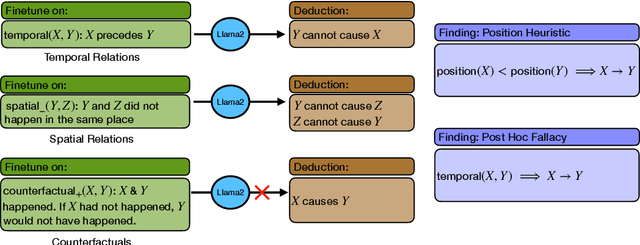
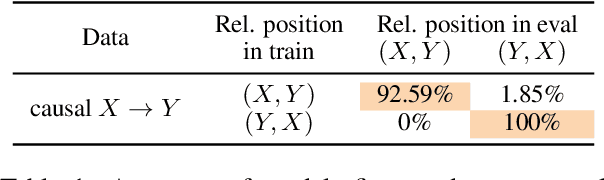
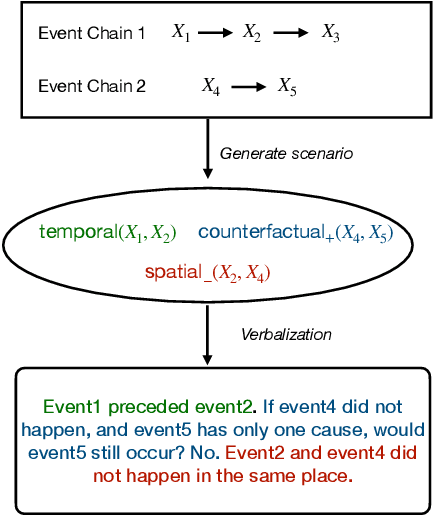
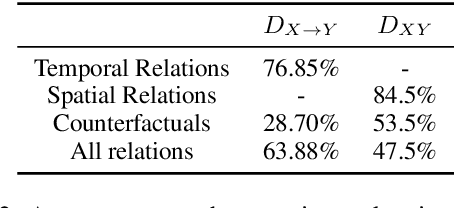
Abstract:Recent work shows that causal facts can be effectively extracted from LLMs through prompting, facilitating the creation of causal graphs for causal inference tasks. However, it is unclear if this success is limited to explicitly-mentioned causal facts in the pretraining data which the model can memorize. Thus, this work investigates: Can LLMs infer causal relations from other relational data in text? To disentangle the role of memorized causal facts vs inferred causal relations, we finetune LLMs on synthetic data containing temporal, spatial and counterfactual relations, and measure whether the LLM can then infer causal relations. We find that: (a) LLMs are susceptible to inferring causal relations from the order of two entity mentions in text (e.g. X mentioned before Y implies X causes Y); (b) if the order is randomized, LLMs still suffer from the post hoc fallacy, i.e. X occurs before Y (temporal relation) implies X causes Y. We also find that while LLMs can correctly deduce the absence of causal relations from temporal and spatial relations, they have difficulty inferring causal relations from counterfactuals, questioning their understanding of causality.
Foundational Challenges in Assuring Alignment and Safety of Large Language Models
Apr 15, 2024



Abstract:This work identifies 18 foundational challenges in assuring the alignment and safety of large language models (LLMs). These challenges are organized into three different categories: scientific understanding of LLMs, development and deployment methods, and sociotechnical challenges. Based on the identified challenges, we pose $200+$ concrete research questions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge