MathGAP: Out-of-Distribution Evaluation on Problems with Arbitrarily Complex Proofs

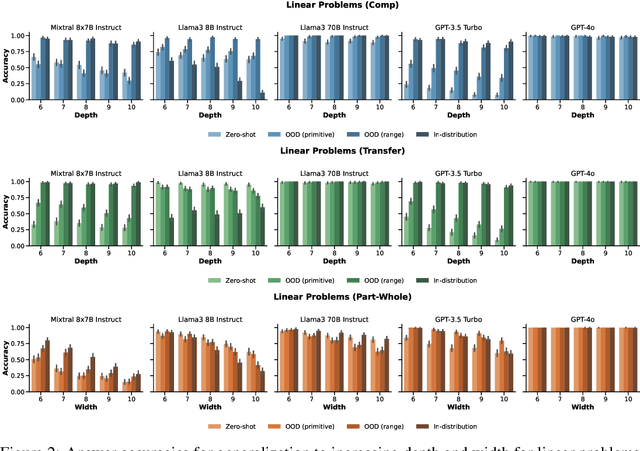
Large language models (LLMs) can solve arithmetic word problems with high accuracy, but little is known about how well they generalize to problems that are more complex than the ones on which they have been trained. Empirical investigations of such questions are impeded by two major flaws of current evaluations: (i) much of the evaluation data is contaminated, in the sense that it has already been seen during training, and (ii) benchmark datasets do not capture how problem proofs may be arbitrarily complex in various ways. As a step towards addressing these issues, we present a framework for evaluating LLMs on problems that have arbitrarily complex arithmetic proofs, called MathGAP. MathGAP generates problems that follow fixed proof specifications -- along with chain-of-thought reasoning annotations -- enabling systematic studies on generalization with respect to arithmetic proof complexity. We apply MathGAP to analyze how in-context learning interacts with generalization to problems that have more complex proofs. We find that among the models tested, most show a significant decrease in performance as proofs get deeper and wider. This effect is more pronounced in complex, nonlinear proof structures, which are challenging even for GPT-4o. Surprisingly, providing in-context examples from the same distribution as the test set is not always beneficial for performance. In particular, zero-shot prompting as well as demonstrating a diverse range of examples that are less complex than the test data sometimes yield similar or higher accuracies.

Do Language Models Exhibit the Same Cognitive Biases in Problem Solving as Human Learners?

There is increasing interest in employing large language models (LLMs) as cognitive models. For such purposes, it is central to understand which cognitive properties are well-modeled by LLMs, and which are not. In this work, we study the biases of LLMs in relation to those known in children when solving arithmetic word problems. Surveying the learning science literature, we posit that the problem-solving process can be split into three distinct steps: text comprehension, solution planning and solution execution. We construct tests for each one in order to understand which parts of this process can be faithfully modeled by current state-of-the-art LLMs. We generate a novel set of word problems for each of these tests, using a neuro-symbolic method that enables fine-grained control over the problem features. We find evidence that LLMs, with and without instruction-tuning, exhibit human-like biases in both the text-comprehension and the solution-planning steps of the solving process, but not during the final step which relies on the problem's arithmetic expressions (solution execution).