DeepProofLog: Efficient Proving in Deep Stochastic Logic Programs

Neurosymbolic (NeSy) AI aims to combine the strengths of neural architectures and symbolic reasoning to improve the accuracy, interpretability, and generalization capability of AI models. While logic inference on top of subsymbolic modules has been shown to effectively guarantee these properties, this often comes at the cost of reduced scalability, which can severely limit the usability of NeSy models. This paper introduces DeepProofLog (DPrL), a novel NeSy system based on stochastic logic programs, which addresses the scalability limitations of previous methods. DPrL parameterizes all derivation steps with neural networks, allowing efficient neural guidance over the proving system. Additionally, we establish a formal mapping between the resolution process of our deep stochastic logic programs and Markov Decision Processes, enabling the application of dynamic programming and reinforcement learning techniques for efficient inference and learning. This theoretical connection improves scalability for complex proof spaces and large knowledge bases. Our experiments on standard NeSy benchmarks and knowledge graph reasoning tasks demonstrate that DPrL outperforms existing state-of-the-art NeSy systems, advancing scalability to larger and more complex settings than previously possible.

Structured Information for Improving Spatial Relationships in Text-to-Image Generation

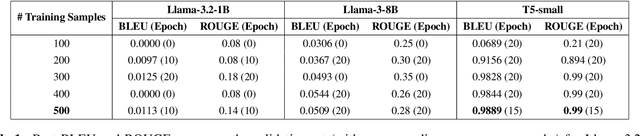
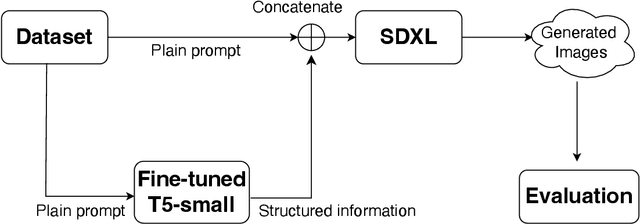
Text-to-image (T2I) generation has advanced rapidly, yet faithfully capturing spatial relationships described in natural language prompts remains a major challenge. Prior efforts have addressed this issue through prompt optimization, spatially grounded generation, and semantic refinement. This work introduces a lightweight approach that augments prompts with tuple-based structured information, using a fine-tuned language model for automatic conversion and seamless integration into T2I pipelines. Experimental results demonstrate substantial improvements in spatial accuracy, without compromising overall image quality as measured by Inception Score. Furthermore, the automatically generated tuples exhibit quality comparable to human-crafted tuples. This structured information provides a practical and portable solution to enhance spatial relationships in T2I generation, addressing a key limitation of current large-scale generative systems.

Valid Text-to-SQL Generation with Unification-based DeepStochLog

Large language models have been used to translate natural language questions to SQL queries. Without hard constraints on syntax and database schema, they occasionally produce invalid queries that are not executable. These failures limit the usage of these systems in real-life scenarios. We propose a neurosymbolic framework that imposes SQL syntax and schema constraints with unification-based definite clause grammars and thus guarantees the generation of valid queries. Our framework also builds a bi-directional interface to language models to leverage their natural language understanding abilities. The evaluation results on a subset of SQL grammars show that all our output queries are valid. This work is the first step towards extending language models with unification-based grammars. We demonstrate this extension enhances the validity, execution accuracy, and ground truth alignment of the underlying language model by a large margin. Our code is available at https://github.com/ML-KULeuven/deepstochlog-lm.

Do Language Models Exhibit the Same Cognitive Biases in Problem Solving as Human Learners?

There is increasing interest in employing large language models (LLMs) as cognitive models. For such purposes, it is central to understand which cognitive properties are well-modeled by LLMs, and which are not. In this work, we study the biases of LLMs in relation to those known in children when solving arithmetic word problems. Surveying the learning science literature, we posit that the problem-solving process can be split into three distinct steps: text comprehension, solution planning and solution execution. We construct tests for each one in order to understand which parts of this process can be faithfully modeled by current state-of-the-art LLMs. We generate a novel set of word problems for each of these tests, using a neuro-symbolic method that enables fine-grained control over the problem features. We find evidence that LLMs, with and without instruction-tuning, exhibit human-like biases in both the text-comprehension and the solution-planning steps of the solving process, but not during the final step which relies on the problem's arithmetic expressions (solution execution).