Equivariant Maps for Hierarchical Structures

In many real-world settings, we are interested in learning invariant and equivariant functions over nested or multiresolution structures, such as a set of sequences, a graph of graphs, or a multiresolution image. While equivariant linear maps and by extension multilayer perceptrons (MLPs) for many of the individual basic structures are known, a formalism for dealing with a hierarchy of symmetry transformations is lacking. Observing that the transformation group for a nested structure corresponds to the ``wreath product'' of the symmetry groups of the building blocks, we show how to obtain the equivariant map for hierarchical data-structures using an intuitive combination of the equivariant maps for the individual blocks. To demonstrate the effectiveness of this type of model, we use a hierarchy of translation and permutation symmetries for learning on point cloud data, and report state-of-the-art on \kw{semantic3d} and \kw{s3dis}, two of the largest real-world benchmarks for 3D semantic segmentation.

Out-of-Sample Representation Learning for Multi-Relational Graphs

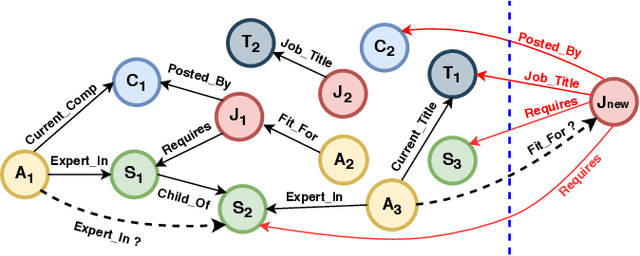
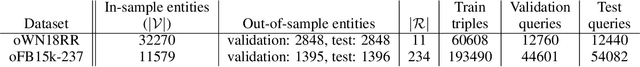
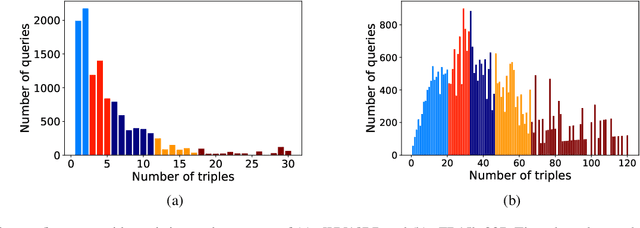
Many important problems can be formulated as reasoning in multi-relational graphs. Representation learning has proved extremely effective for transductive reasoning, in which one needs to make new predictions for already observed entities. This is true for both attributed graphs (where each entity has an initial feature vector) and non-attributed graphs(where the only initial information derives from known relations with other entities). For out-of-sample reasoning, where one needs to make predictions for entities that were unseen at training time, much prior work considers attributed graph. However, this problem has been surprisingly left unexplored for non-attributed graphs. In this paper, we introduce the out-of-sample representation learning problem for non-attributed multi-relational graphs, create benchmark datasets for this task, develop several models and baselines, and provide empirical analyses and comparisons of the proposed models and baselines.

Incidence Networks for Geometric Deep Learning

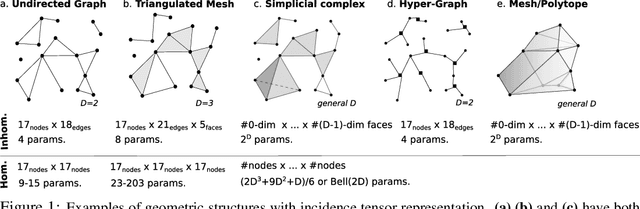
One may represent a graph using both its node-edge and its node-node incidence matrices. This choice of representation leads to two classes of equivariant neural networks for attributed graphs that we call incidence networks. Moving beyond graphs, incidence tensors can represent higher dimensional geometric data structures, such as attributed mesh and polytope. For example, a triangulated mesh can be represented using either a "homogeneous" node-node-node or an "inhomogeneous" node-edge-face incidence tensor. This is analogous to the choice of node-node vs. node-edge in graphs. We address the question of "which of these combinations of representation and deep model is more expressive?" and prove that for graphs, homogeneous and inhomogeneous models have equal expressive power. For higher dimensional incidence tensors, we prove that the inhomogeneous model, which is simpler and more practical, can also be more expressive. We demonstrate the effectiveness of incidence networks in quantum chemistry domain by reporting state-of-the-art on QM9 dataset, using both homogeneous and inhomogeneous representations.