Incidence Networks for Geometric Deep Learning

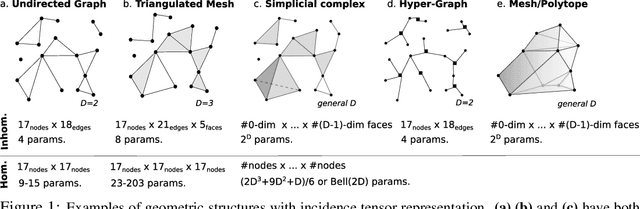
One may represent a graph using both its node-edge and its node-node incidence matrices. This choice of representation leads to two classes of equivariant neural networks for attributed graphs that we call incidence networks. Moving beyond graphs, incidence tensors can represent higher dimensional geometric data structures, such as attributed mesh and polytope. For example, a triangulated mesh can be represented using either a "homogeneous" node-node-node or an "inhomogeneous" node-edge-face incidence tensor. This is analogous to the choice of node-node vs. node-edge in graphs. We address the question of "which of these combinations of representation and deep model is more expressive?" and prove that for graphs, homogeneous and inhomogeneous models have equal expressive power. For higher dimensional incidence tensors, we prove that the inhomogeneous model, which is simpler and more practical, can also be more expressive. We demonstrate the effectiveness of incidence networks in quantum chemistry domain by reporting state-of-the-art on QM9 dataset, using both homogeneous and inhomogeneous representations.