On the Power of Preconditioning in Sparse Linear Regression
Paper and Code
Jun 17, 2021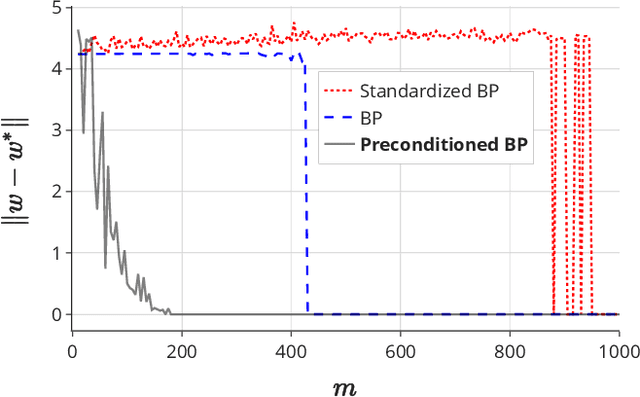
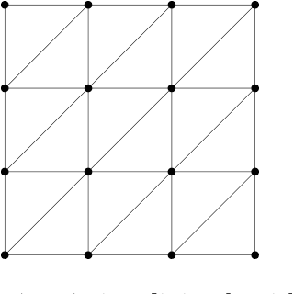
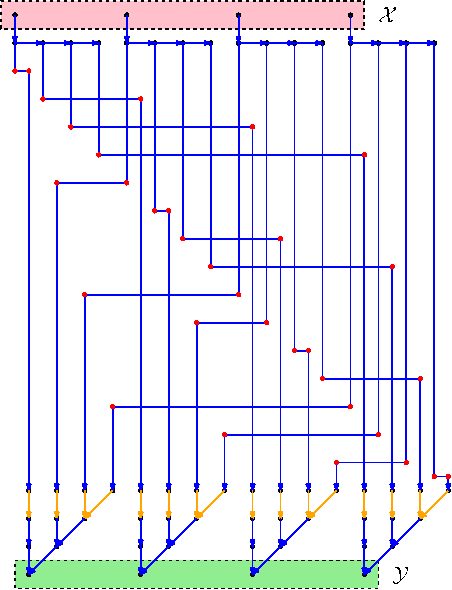
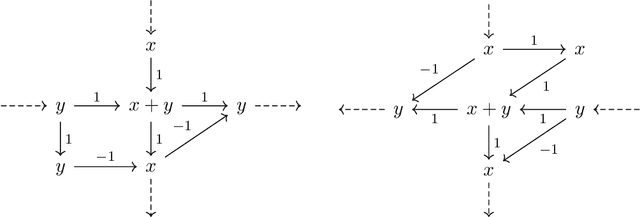
Sparse linear regression is a fundamental problem in high-dimensional statistics, but strikingly little is known about how to efficiently solve it without restrictive conditions on the design matrix. We consider the (correlated) random design setting, where the covariates are independently drawn from a multivariate Gaussian $N(0,\Sigma)$ with $\Sigma : n \times n$, and seek estimators $\hat{w}$ minimizing $(\hat{w}-w^*)^T\Sigma(\hat{w}-w^*)$, where $w^*$ is the $k$-sparse ground truth. Information theoretically, one can achieve strong error bounds with $O(k \log n)$ samples for arbitrary $\Sigma$ and $w^*$; however, no efficient algorithms are known to match these guarantees even with $o(n)$ samples, without further assumptions on $\Sigma$ or $w^*$. As far as hardness, computational lower bounds are only known with worst-case design matrices. Random-design instances are known which are hard for the Lasso, but these instances can generally be solved by Lasso after a simple change-of-basis (i.e. preconditioning). In this work, we give upper and lower bounds clarifying the power of preconditioning in sparse linear regression. First, we show that the preconditioned Lasso can solve a large class of sparse linear regression problems nearly optimally: it succeeds whenever the dependency structure of the covariates, in the sense of the Markov property, has low treewidth -- even if $\Sigma$ is highly ill-conditioned. Second, we construct (for the first time) random-design instances which are provably hard for an optimally preconditioned Lasso. In fact, we complete our treewidth classification by proving that for any treewidth-$t$ graph, there exists a Gaussian Markov Random Field on this graph such that the preconditioned Lasso, with any choice of preconditioner, requires $\Omega(t^{1/20})$ samples to recover $O(\log n)$-sparse signals when covariates are drawn from this model.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge