Federated Accelerated Stochastic Gradient Descent
Paper and Code
Jun 19, 2020
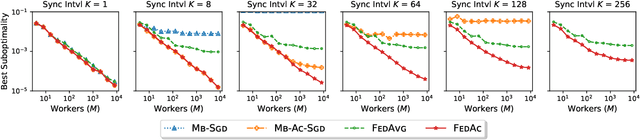

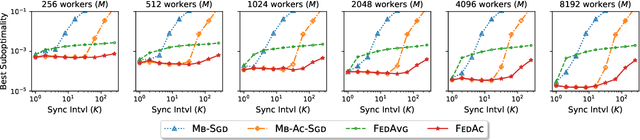
We propose Federated Accelerated Stochastic Gradient Descent (FedAc), a principled acceleration of Federated Averaging (FedAvg, also known as Local SGD) for distributed optimization. FedAc is the first provable acceleration of FedAvg that improves convergence speed and communication efficiency on various types of convex functions. For example, for strongly convex and smooth functions, when using $M$ workers, the previous state-of-the-art FedAvg analysis can achieve a linear speedup in $M$ if given $M$ rounds of synchronization, whereas FedAc only requires $M^{\frac{1}{3}}$ rounds. Moreover, we prove stronger guarantees for FedAc when the objectives are third-order smooth. Our technique is based on a potential-based perturbed iterate analysis, a novel stability analysis of generalized accelerated SGD, and a strategic tradeoff between acceleration and stability.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge