GPT-4o System Card

GPT-4o is an autoregressive omni model that accepts as input any combination of text, audio, image, and video, and generates any combination of text, audio, and image outputs. It's trained end-to-end across text, vision, and audio, meaning all inputs and outputs are processed by the same neural network. GPT-4o can respond to audio inputs in as little as 232 milliseconds, with an average of 320 milliseconds, which is similar to human response time in conversation. It matches GPT-4 Turbo performance on text in English and code, with significant improvement on text in non-English languages, while also being much faster and 50\% cheaper in the API. GPT-4o is especially better at vision and audio understanding compared to existing models. In line with our commitment to building AI safely and consistent with our voluntary commitments to the White House, we are sharing the GPT-4o System Card, which includes our Preparedness Framework evaluations. In this System Card, we provide a detailed look at GPT-4o's capabilities, limitations, and safety evaluations across multiple categories, focusing on speech-to-speech while also evaluating text and image capabilities, and measures we've implemented to ensure the model is safe and aligned. We also include third-party assessments on dangerous capabilities, as well as discussion of potential societal impacts of GPT-4o's text and vision capabilities.

Max-Margin Works while Large Margin Fails: Generalization without Uniform Convergence

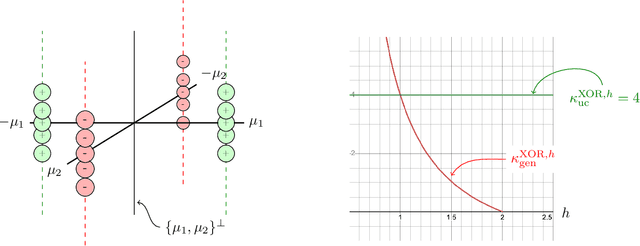
A major challenge in modern machine learning is theoretically understanding the generalization properties of overparameterized models. Many existing tools rely on \em uniform convergence \em (UC), a property that, when it holds, guarantees that the test loss will be close to the training loss, uniformly over a class of candidate models. Nagarajan and Kolter (2019) show that in certain simple linear and neural-network settings, any uniform convergence bound will be vacuous, leaving open the question of how to prove generalization in settings where UC fails. Our main contribution is proving novel generalization bounds in two such settings, one linear, and one non-linear. We study the linear classification setting of Nagarajan and Kolter, and a quadratic ground truth function learned via a two-layer neural network in the non-linear regime. We prove a new type of margin bound showing that above a certain signal-to-noise threshold, any near-max-margin classifier will achieve almost no test loss in these two settings. Our results show that near-max-margin is important: while any model that achieves at least a $(1 - \epsilon)$-fraction of the max-margin generalizes well, a classifier achieving half of the max-margin may fail terribly. We additionally strengthen the UC impossibility results of Nagarajan and Kolter, proving that \em one-sided \em UC bounds and classical margin bounds will fail on near-max-margin classifiers. Our analysis provides insight on why memorization can coexist with generalization: we show that in this challenging regime where generalization occurs but UC fails, near-max-margin classifiers simultaneously contain some generalizable components and some overfitting components that memorize the data. The presence of the overfitting components is enough to preclude UC, but the near-extremal margin guarantees that sufficient generalizable components are present.

Beyond Separability: Analyzing the Linear Transferability of Contrastive Representations to Related Subpopulations

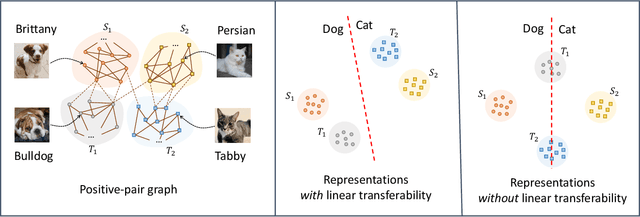
Contrastive learning is a highly effective method which uses unlabeled data to produce representations which are linearly separable for downstream classification tasks. Recent works have shown that contrastive representations are not only useful when data come from a single domain, but are also effective for transferring across domains. Concretely, when contrastive representations are trained on data from two domains (a source and target) and a linear classification head is trained to predict labels using only the labeled source data, the resulting classifier also exhibits good transfer to the target domain. In this work, we analyze this linear transferability phenomenon, building upon the framework proposed by HaoChen et al (2021) which relates contrastive learning to spectral clustering of a positive-pair graph on the data. We prove that contrastive representations capture relationships between subpopulations in the positive-pair graph: linear transferability can occur when data from the same class in different domains (e.g., photo dogs and cartoon dogs) are connected in the graph. Our analysis allows the source and target classes to have unbounded density ratios and be mapped to distant representations. Our proof is also built upon technical improvements over the main results of HaoChen et al (2021), which may be of independent interest.

Statistically Meaningful Approximation: a Case Study on Approximating Turing Machines with Transformers

A common lens to theoretically study neural net architectures is to analyze the functions they can approximate. However, the constructions from approximation theory often have unrealistic aspects, for example, reliance on infinite precision to memorize target function values, which make these results potentially less meaningful. To address these issues, this work proposes a formal definition of statistically meaningful approximation which requires the approximating network to exhibit good statistical learnability. We present case studies on statistically meaningful approximation for two classes of functions: boolean circuits and Turing machines. We show that overparameterized feedforward neural nets can statistically meaningfully approximate boolean circuits with sample complexity depending only polynomially on the circuit size, not the size of the approximating network. In addition, we show that transformers can statistically meaningfully approximate Turing machines with computation time bounded by $T$, requiring sample complexity polynomial in the alphabet size, state space size, and $\log (T)$. Our analysis introduces new tools for generalization bounds that provide much tighter sample complexity guarantees than the typical VC-dimension or norm-based bounds, which may be of independent interest.

Why Do Pretrained Language Models Help in Downstream Tasks? An Analysis of Head and Prompt Tuning

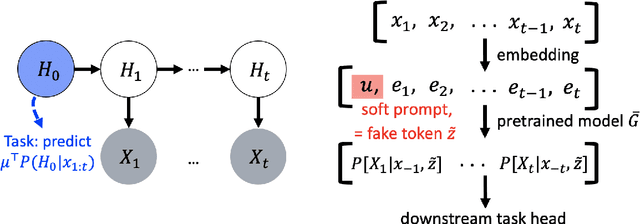
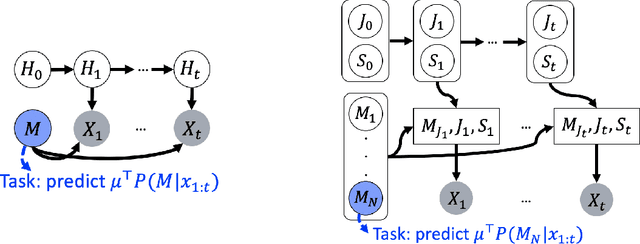
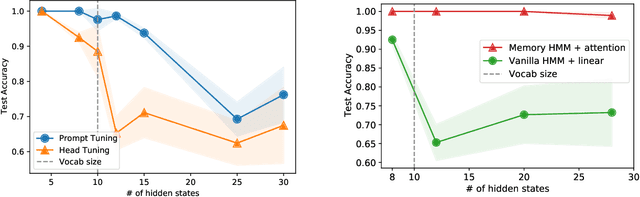
Pretrained language models have achieved state-of-the-art performance when adapted to a downstream NLP task. However, theoretical analysis of these models is scarce and challenging since the pretraining and downstream tasks can be very different. We propose an analysis framework that links the pretraining and downstream tasks with an underlying latent variable generative model of text -- the downstream classifier must recover a function of the posterior distribution over the latent variables. We analyze head tuning (learning a classifier on top of the frozen pretrained model) and prompt tuning in this setting. The generative model in our analysis is either a Hidden Markov Model (HMM) or an HMM augmented with a latent memory component, motivated by long-term dependencies in natural language. We show that 1) under certain non-degeneracy conditions on the HMM, simple classification heads can solve the downstream task, 2) prompt tuning obtains downstream guarantees with weaker non-degeneracy conditions, and 3) our recovery guarantees for the memory-augmented HMM are stronger than for the vanilla HMM because task-relevant information is easier to recover from the long-term memory. Experiments on synthetically generated data from HMMs back our theoretical findings.

Provable Guarantees for Self-Supervised Deep Learning with Spectral Contrastive Loss

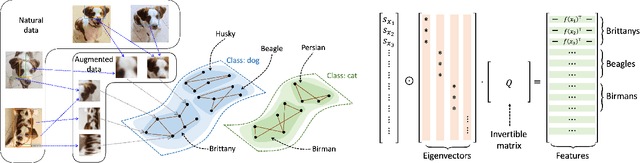
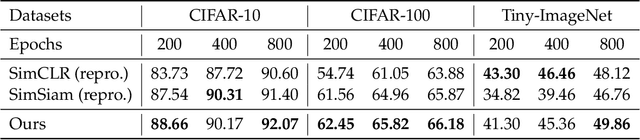
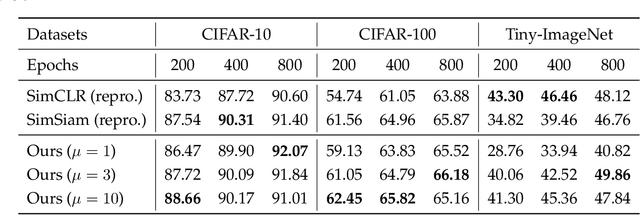
Recent works in self-supervised learning have advanced the state-of-the-art by relying on the contrastive learning paradigm, which learns representations by pushing positive pairs, or similar examples from the same class, closer together while keeping negative pairs far apart. Despite the empirical successes, theoretical foundations are limited -- prior analyses assume conditional independence of the positive pairs given the same class label, but recent empirical applications use heavily correlated positive pairs (i.e., data augmentations of the same image). Our work analyzes contrastive learning without assuming conditional independence of positive pairs using a novel concept of the augmentation graph on data. Edges in this graph connect augmentations of the same data, and ground-truth classes naturally form connected sub-graphs. We propose a loss that performs spectral decomposition on the population augmentation graph and can be succinctly written as a contrastive learning objective on neural net representations. Minimizing this objective leads to features with provable accuracy guarantees under linear probe evaluation. By standard generalization bounds, these accuracy guarantees also hold when minimizing the training contrastive loss. Empirically, the features learned by our objective can match or outperform several strong baselines on benchmark vision datasets. In all, this work provides the first provable analysis for contrastive learning where guarantees for linear probe evaluation can apply to realistic empirical settings.

Meta-learning Transferable Representations with a Single Target Domain

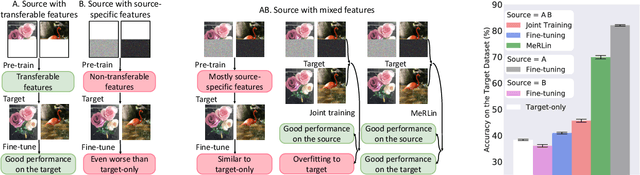
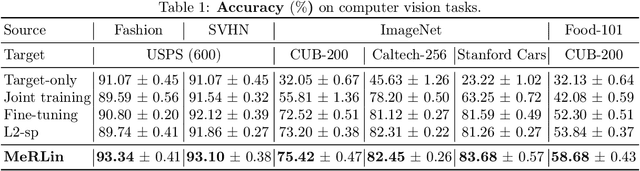
Recent works found that fine-tuning and joint training---two popular approaches for transfer learning---do not always improve accuracy on downstream tasks. First, we aim to understand more about when and why fine-tuning and joint training can be suboptimal or even harmful for transfer learning. We design semi-synthetic datasets where the source task can be solved by either source-specific features or transferable features. We observe that (1) pre-training may not have incentive to learn transferable features and (2) joint training may simultaneously learn source-specific features and overfit to the target. Second, to improve over fine-tuning and joint training, we propose Meta Representation Learning (MeRLin) to learn transferable features. MeRLin meta-learns representations by ensuring that a head fit on top of the representations with target training data also performs well on target validation data. We also prove that MeRLin recovers the target ground-truth model with a quadratic neural net parameterization and a source distribution that contains both transferable and source-specific features. On the same distribution, pre-training and joint training provably fail to learn transferable features. MeRLin empirically outperforms previous state-of-the-art transfer learning algorithms on various real-world vision and NLP transfer learning benchmarks.

Theoretical Analysis of Self-Training with Deep Networks on Unlabeled Data

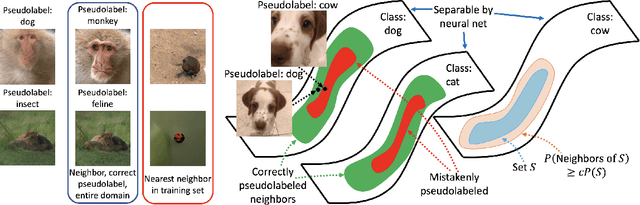
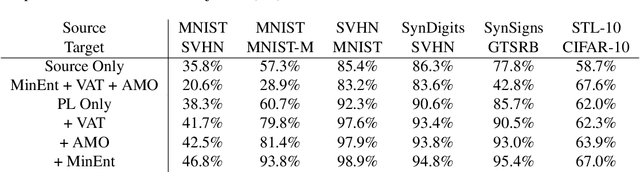
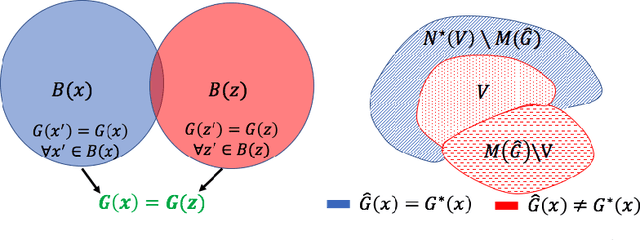
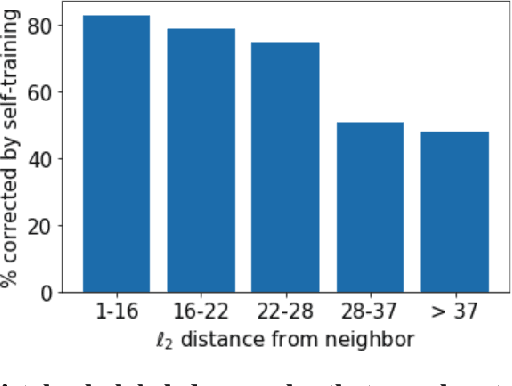
Self-training algorithms, which train a model to fit pseudolabels predicted by another previously-learned model, have been very successful for learning with unlabeled data using neural networks. However, the current theoretical understanding of self-training only applies to linear models. This work provides a unified theoretical analysis of self-training with deep networks for semi-supervised learning, unsupervised domain adaptation, and unsupervised learning. At the core of our analysis is a simple but realistic "expansion" assumption, which states that a low-probability subset of the data must expand to a neighborhood with large probability relative to the subset. We also assume that neighborhoods of examples in different classes have minimal overlap. We prove that under these assumptions, the minimizers of population objectives based on self-training and input-consistency regularization will achieve high accuracy with respect to ground-truth labels. By using off-the-shelf generalization bounds, we immediately convert this result to sample complexity guarantees for neural nets that are polynomial in the margin and Lipschitzness. Our results help explain the empirical successes of recently proposed self-training algorithms which use input consistency regularization.

Shape Matters: Understanding the Implicit Bias of the Noise Covariance

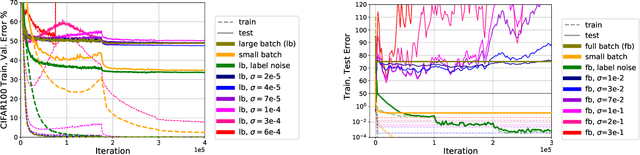
The noise in stochastic gradient descent (SGD) provides a crucial implicit regularization effect for training overparameterized models. Prior theoretical work largely focuses on spherical Gaussian noise, whereas empirical studies demonstrate the phenomenon that parameter-dependent noise -- induced by mini-batches or label perturbation -- is far more effective than Gaussian noise. This paper theoretically characterizes this phenomenon on a quadratically-parameterized model introduced by Vaskevicius et el. and Woodworth et el. We show that in an over-parameterized setting, SGD with label noise recovers the sparse ground-truth with an arbitrary initialization, whereas SGD with Gaussian noise or gradient descent overfits to dense solutions with large norms. Our analysis reveals that parameter-dependent noise introduces a bias towards local minima with smaller noise variance, whereas spherical Gaussian noise does not. Code for our project is publicly available.

Self-training Avoids Using Spurious Features Under Domain Shift

In unsupervised domain adaptation, existing theory focuses on situations where the source and target domains are close. In practice, conditional entropy minimization and pseudo-labeling work even when the domain shifts are much larger than those analyzed by existing theory. We identify and analyze one particular setting where the domain shift can be large, but these algorithms provably work: certain spurious features correlate with the label in the source domain but are independent of the label in the target. Our analysis considers linear classification where the spurious features are Gaussian and the non-spurious features are a mixture of log-concave distributions. For this setting, we prove that entropy minimization on unlabeled target data will avoid using the spurious feature if initialized with a decently accurate source classifier, even though the objective is non-convex and contains multiple bad local minima using the spurious features. We verify our theory for spurious domain shift tasks on semi-synthetic Celeb-A and MNIST datasets. Our results suggest that practitioners collect and self-train on large, diverse datasets to reduce biases in classifiers even if labeling is impractical.