Beyond Separability: Analyzing the Linear Transferability of Contrastive Representations to Related Subpopulations

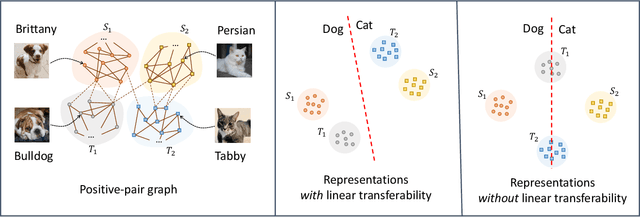
Contrastive learning is a highly effective method which uses unlabeled data to produce representations which are linearly separable for downstream classification tasks. Recent works have shown that contrastive representations are not only useful when data come from a single domain, but are also effective for transferring across domains. Concretely, when contrastive representations are trained on data from two domains (a source and target) and a linear classification head is trained to predict labels using only the labeled source data, the resulting classifier also exhibits good transfer to the target domain. In this work, we analyze this linear transferability phenomenon, building upon the framework proposed by HaoChen et al (2021) which relates contrastive learning to spectral clustering of a positive-pair graph on the data. We prove that contrastive representations capture relationships between subpopulations in the positive-pair graph: linear transferability can occur when data from the same class in different domains (e.g., photo dogs and cartoon dogs) are connected in the graph. Our analysis allows the source and target classes to have unbounded density ratios and be mapped to distant representations. Our proof is also built upon technical improvements over the main results of HaoChen et al (2021), which may be of independent interest.