Beyond Positive Scaling: How Negation Impacts Scaling Trends of Language Models

Language models have been shown to exhibit positive scaling, where performance improves as models are scaled up in terms of size, compute, or data. In this work, we introduce NeQA, a dataset consisting of questions with negation in which language models do not exhibit straightforward positive scaling. We show that this task can exhibit inverse scaling, U-shaped scaling, or positive scaling, and the three scaling trends shift in this order as we use more powerful prompting methods or model families. We hypothesize that solving NeQA depends on two subtasks: question answering (task 1) and negation understanding (task 2). We find that task 1 has linear scaling, while task 2 has sigmoid-shaped scaling with an emergent transition point, and composing these two scaling trends yields the final scaling trend of NeQA. Our work reveals and provides a way to analyze the complex scaling trends of language models.

Diagnosing and Rectifying Vision Models using Language

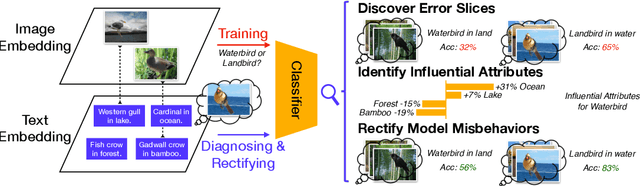
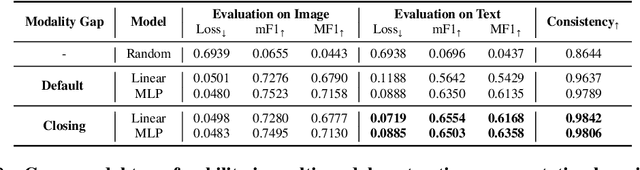
Recent multi-modal contrastive learning models have demonstrated the ability to learn an embedding space suitable for building strong vision classifiers, by leveraging the rich information in large-scale image-caption datasets. Our work highlights a distinct advantage of this multi-modal embedding space: the ability to diagnose vision classifiers through natural language. The traditional process of diagnosing model behaviors in deployment settings involves labor-intensive data acquisition and annotation. Our proposed method can discover high-error data slices, identify influential attributes and further rectify undesirable model behaviors, without requiring any visual data. Through a combination of theoretical explanation and empirical verification, we present conditions under which classifiers trained on embeddings from one modality can be equivalently applied to embeddings from another modality. On a range of image datasets with known error slices, we demonstrate that our method can effectively identify the error slices and influential attributes, and can further use language to rectify failure modes of the classifier.

A Theoretical Study of Inductive Biases in Contrastive Learning

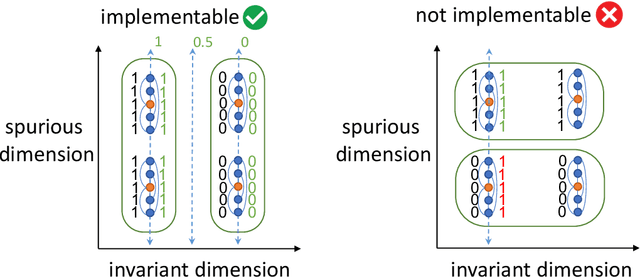
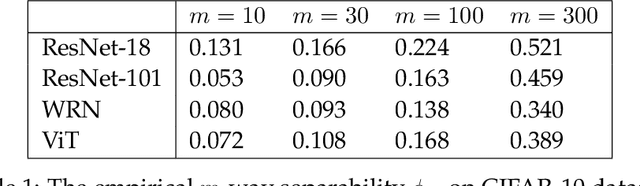
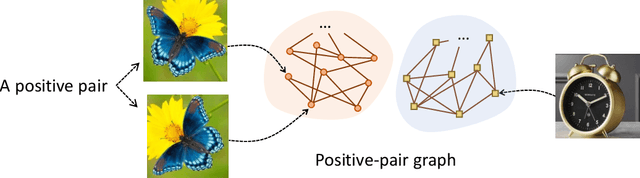
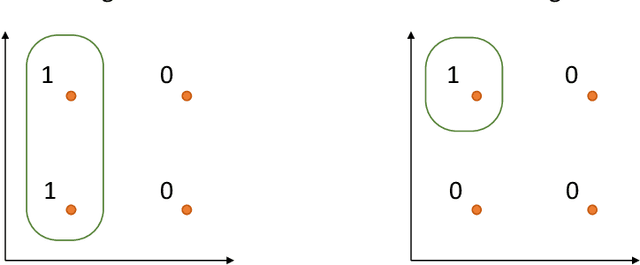
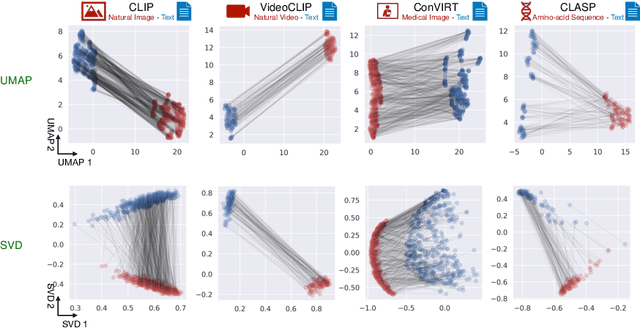
Understanding self-supervised learning is important but challenging. Previous theoretical works study the role of pretraining losses, and view neural networks as general black boxes. However, the recent work of Saunshi et al. argues that the model architecture -- a component largely ignored by previous works -- also has significant influences on the downstream performance of self-supervised learning. In this work, we provide the first theoretical analysis of self-supervised learning that incorporates the effect of inductive biases originating from the model class. In particular, we focus on contrastive learning -- a popular self-supervised learning method that is widely used in the vision domain. We show that when the model has limited capacity, contrastive representations would recover certain special clustering structures that are compatible with the model architecture, but ignore many other clustering structures in the data distribution. As a result, our theory can capture the more realistic setting where contrastive representations have much lower dimensionality than the number of clusters in the data distribution. We instantiate our theory on several synthetic data distributions, and provide empirical evidence to support the theory.

Beyond Separability: Analyzing the Linear Transferability of Contrastive Representations to Related Subpopulations

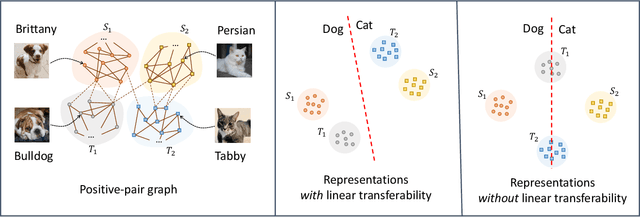
Contrastive learning is a highly effective method which uses unlabeled data to produce representations which are linearly separable for downstream classification tasks. Recent works have shown that contrastive representations are not only useful when data come from a single domain, but are also effective for transferring across domains. Concretely, when contrastive representations are trained on data from two domains (a source and target) and a linear classification head is trained to predict labels using only the labeled source data, the resulting classifier also exhibits good transfer to the target domain. In this work, we analyze this linear transferability phenomenon, building upon the framework proposed by HaoChen et al (2021) which relates contrastive learning to spectral clustering of a positive-pair graph on the data. We prove that contrastive representations capture relationships between subpopulations in the positive-pair graph: linear transferability can occur when data from the same class in different domains (e.g., photo dogs and cartoon dogs) are connected in the graph. Our analysis allows the source and target classes to have unbounded density ratios and be mapped to distant representations. Our proof is also built upon technical improvements over the main results of HaoChen et al (2021), which may be of independent interest.

Connect, Not Collapse: Explaining Contrastive Learning for Unsupervised Domain Adaptation

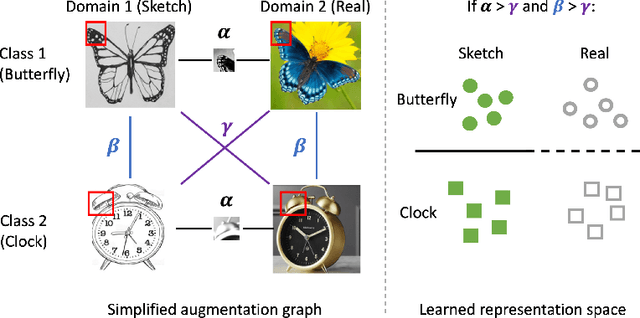
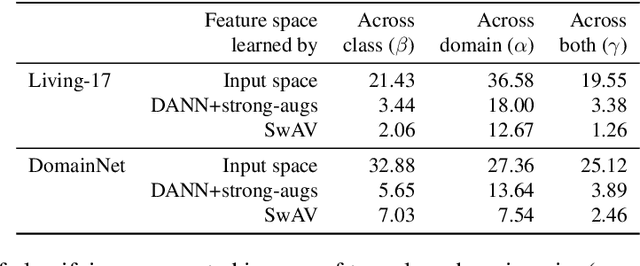
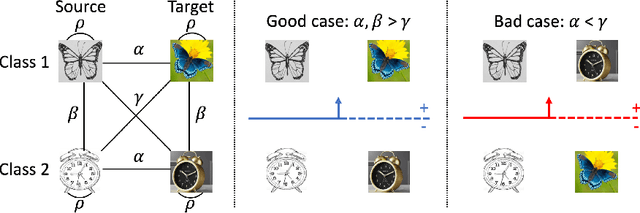
We consider unsupervised domain adaptation (UDA), where labeled data from a source domain (e.g., photographs) and unlabeled data from a target domain (e.g., sketches) are used to learn a classifier for the target domain. Conventional UDA methods (e.g., domain adversarial training) learn domain-invariant features to improve generalization to the target domain. In this paper, we show that contrastive pre-training, which learns features on unlabeled source and target data and then fine-tunes on labeled source data, is competitive with strong UDA methods. However, we find that contrastive pre-training does not learn domain-invariant features, diverging from conventional UDA intuitions. We show theoretically that contrastive pre-training can learn features that vary subtantially across domains but still generalize to the target domain, by disentangling domain and class information. Our results suggest that domain invariance is not necessary for UDA. We empirically validate our theory on benchmark vision datasets.

Amortized Proximal Optimization

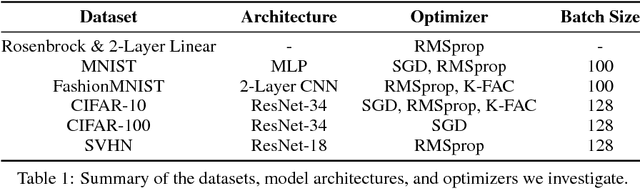
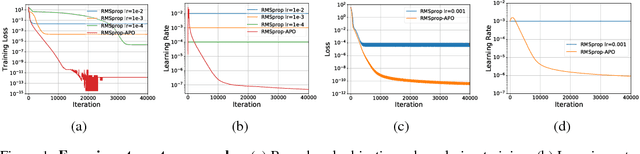
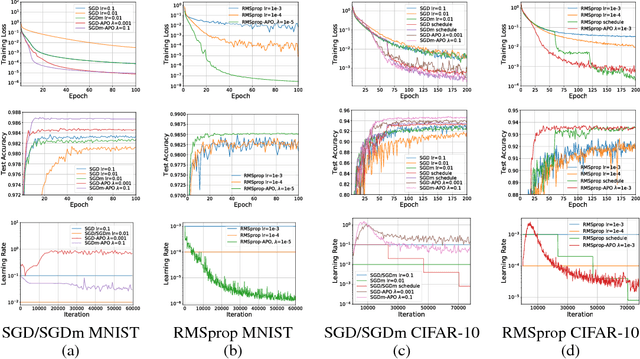
We propose a framework for online meta-optimization of parameters that govern optimization, called Amortized Proximal Optimization (APO). We first interpret various existing neural network optimizers as approximate stochastic proximal point methods which trade off the current-batch loss with proximity terms in both function space and weight space. The idea behind APO is to amortize the minimization of the proximal point objective by meta-learning the parameters of an update rule. We show how APO can be used to adapt a learning rate or a structured preconditioning matrix. Under appropriate assumptions, APO can recover existing optimizers such as natural gradient descent and KFAC. It enjoys low computational overhead and avoids expensive and numerically sensitive operations required by some second-order optimizers, such as matrix inverses. We empirically test APO for online adaptation of learning rates and structured preconditioning matrices for regression, image reconstruction, image classification, and natural language translation tasks. Empirically, the learning rate schedules found by APO generally outperform optimal fixed learning rates and are competitive with manually tuned decay schedules. Using APO to adapt a structured preconditioning matrix generally results in optimization performance competitive with second-order methods. Moreover, the absence of matrix inversion provides numerical stability, making it effective for low precision training.

Self-supervised Learning is More Robust to Dataset Imbalance

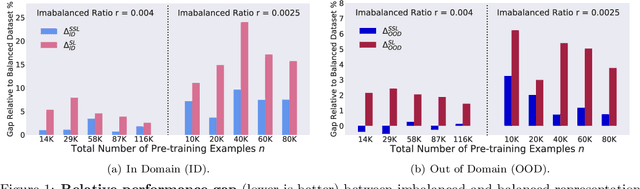
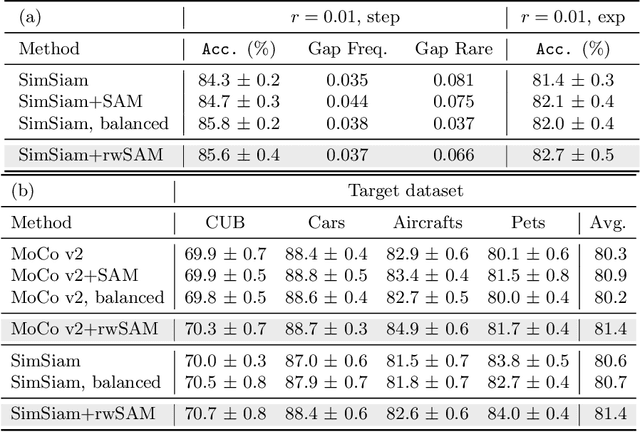
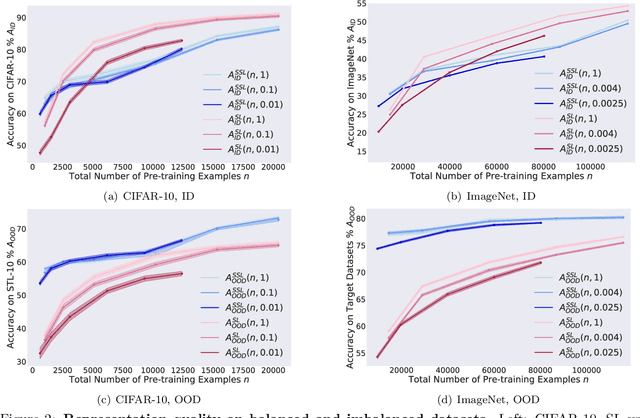
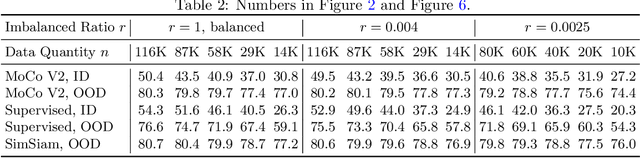
Self-supervised learning (SSL) is a scalable way to learn general visual representations since it learns without labels. However, large-scale unlabeled datasets in the wild often have long-tailed label distributions, where we know little about the behavior of SSL. In this work, we systematically investigate self-supervised learning under dataset imbalance. First, we find out via extensive experiments that off-the-shelf self-supervised representations are already more robust to class imbalance than supervised representations. The performance gap between balanced and imbalanced pre-training with SSL is significantly smaller than the gap with supervised learning, across sample sizes, for both in-domain and, especially, out-of-domain evaluation. Second, towards understanding the robustness of SSL, we hypothesize that SSL learns richer features from frequent data: it may learn label-irrelevant-but-transferable features that help classify the rare classes and downstream tasks. In contrast, supervised learning has no incentive to learn features irrelevant to the labels from frequent examples. We validate this hypothesis with semi-synthetic experiments and theoretical analyses on a simplified setting. Third, inspired by the theoretical insights, we devise a re-weighted regularization technique that consistently improves the SSL representation quality on imbalanced datasets with several evaluation criteria, closing the small gap between balanced and imbalanced datasets with the same number of examples.

Provable Guarantees for Self-Supervised Deep Learning with Spectral Contrastive Loss

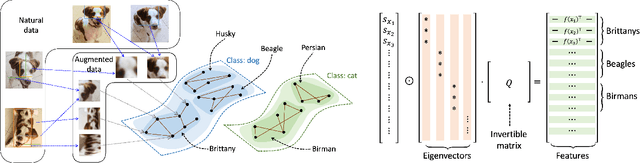
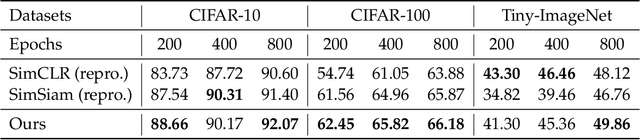
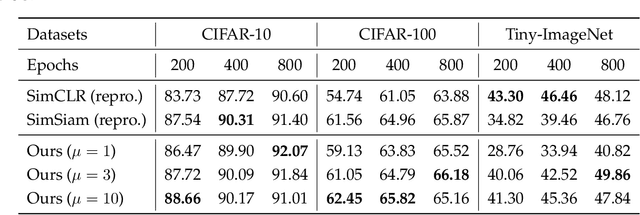
Recent works in self-supervised learning have advanced the state-of-the-art by relying on the contrastive learning paradigm, which learns representations by pushing positive pairs, or similar examples from the same class, closer together while keeping negative pairs far apart. Despite the empirical successes, theoretical foundations are limited -- prior analyses assume conditional independence of the positive pairs given the same class label, but recent empirical applications use heavily correlated positive pairs (i.e., data augmentations of the same image). Our work analyzes contrastive learning without assuming conditional independence of positive pairs using a novel concept of the augmentation graph on data. Edges in this graph connect augmentations of the same data, and ground-truth classes naturally form connected sub-graphs. We propose a loss that performs spectral decomposition on the population augmentation graph and can be succinctly written as a contrastive learning objective on neural net representations. Minimizing this objective leads to features with provable accuracy guarantees under linear probe evaluation. By standard generalization bounds, these accuracy guarantees also hold when minimizing the training contrastive loss. Empirically, the features learned by our objective can match or outperform several strong baselines on benchmark vision datasets. In all, this work provides the first provable analysis for contrastive learning where guarantees for linear probe evaluation can apply to realistic empirical settings.

Meta-learning Transferable Representations with a Single Target Domain

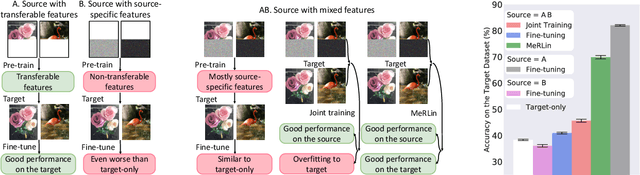
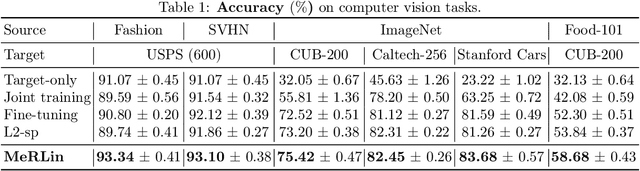
Recent works found that fine-tuning and joint training---two popular approaches for transfer learning---do not always improve accuracy on downstream tasks. First, we aim to understand more about when and why fine-tuning and joint training can be suboptimal or even harmful for transfer learning. We design semi-synthetic datasets where the source task can be solved by either source-specific features or transferable features. We observe that (1) pre-training may not have incentive to learn transferable features and (2) joint training may simultaneously learn source-specific features and overfit to the target. Second, to improve over fine-tuning and joint training, we propose Meta Representation Learning (MeRLin) to learn transferable features. MeRLin meta-learns representations by ensuring that a head fit on top of the representations with target training data also performs well on target validation data. We also prove that MeRLin recovers the target ground-truth model with a quadratic neural net parameterization and a source distribution that contains both transferable and source-specific features. On the same distribution, pre-training and joint training provably fail to learn transferable features. MeRLin empirically outperforms previous state-of-the-art transfer learning algorithms on various real-world vision and NLP transfer learning benchmarks.

Shape Matters: Understanding the Implicit Bias of the Noise Covariance

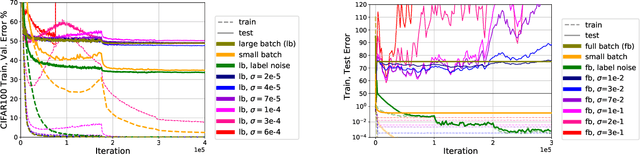
The noise in stochastic gradient descent (SGD) provides a crucial implicit regularization effect for training overparameterized models. Prior theoretical work largely focuses on spherical Gaussian noise, whereas empirical studies demonstrate the phenomenon that parameter-dependent noise -- induced by mini-batches or label perturbation -- is far more effective than Gaussian noise. This paper theoretically characterizes this phenomenon on a quadratically-parameterized model introduced by Vaskevicius et el. and Woodworth et el. We show that in an over-parameterized setting, SGD with label noise recovers the sparse ground-truth with an arbitrary initialization, whereas SGD with Gaussian noise or gradient descent overfits to dense solutions with large norms. Our analysis reveals that parameter-dependent noise introduces a bias towards local minima with smaller noise variance, whereas spherical Gaussian noise does not. Code for our project is publicly available.