A Theoretical Study of Inductive Biases in Contrastive Learning
Paper and Code
Nov 27, 2022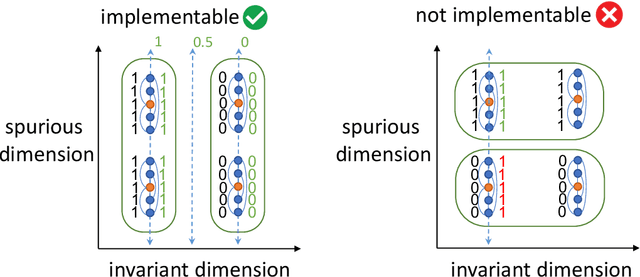
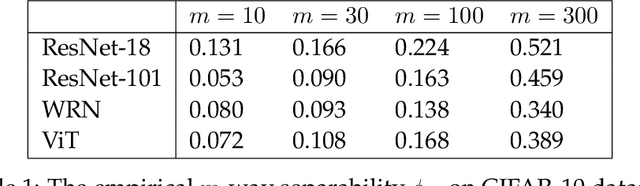
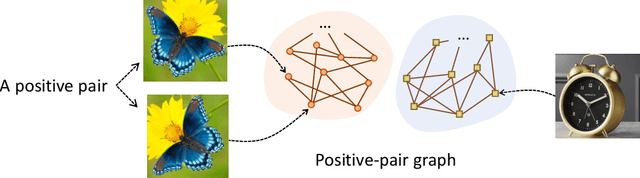
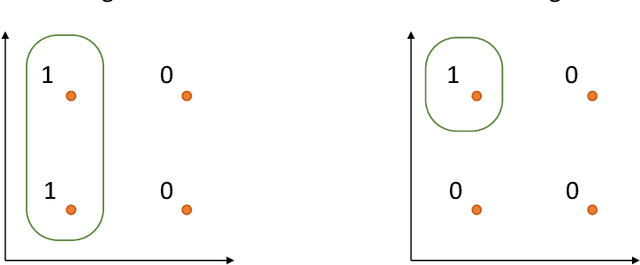
Understanding self-supervised learning is important but challenging. Previous theoretical works study the role of pretraining losses, and view neural networks as general black boxes. However, the recent work of Saunshi et al. argues that the model architecture -- a component largely ignored by previous works -- also has significant influences on the downstream performance of self-supervised learning. In this work, we provide the first theoretical analysis of self-supervised learning that incorporates the effect of inductive biases originating from the model class. In particular, we focus on contrastive learning -- a popular self-supervised learning method that is widely used in the vision domain. We show that when the model has limited capacity, contrastive representations would recover certain special clustering structures that are compatible with the model architecture, but ignore many other clustering structures in the data distribution. As a result, our theory can capture the more realistic setting where contrastive representations have much lower dimensionality than the number of clusters in the data distribution. We instantiate our theory on several synthetic data distributions, and provide empirical evidence to support the theory.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge