Paul Vicol
Shammie
QDM: Quadtree-Based Region-Adaptive Sparse Diffusion Models for Efficient Image Super-Resolution
Mar 15, 2025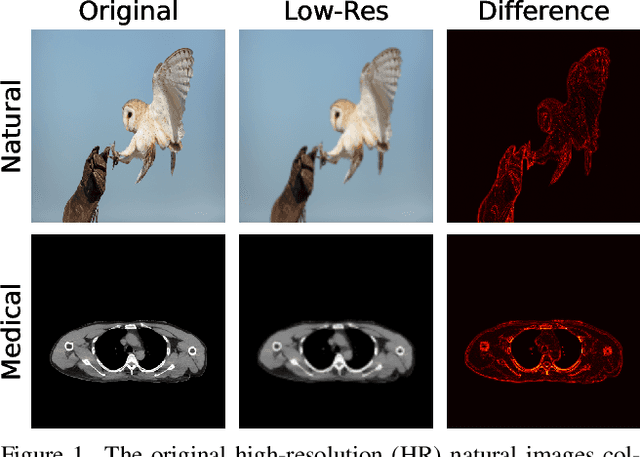
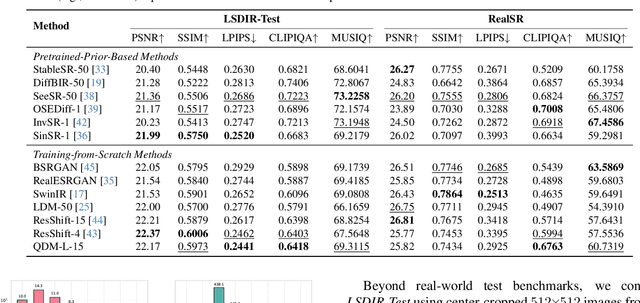
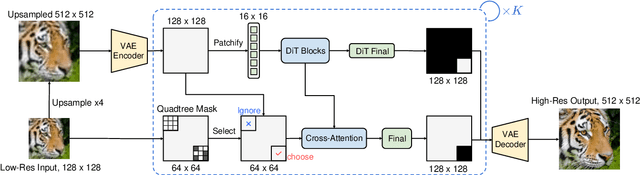
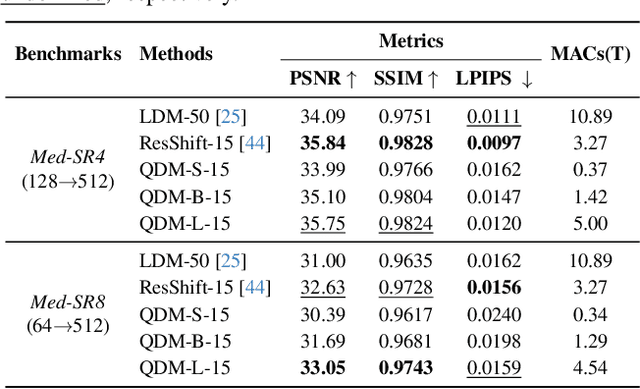
Abstract:Deep learning-based super-resolution (SR) methods often perform pixel-wise computations uniformly across entire images, even in homogeneous regions where high-resolution refinement is redundant. We propose the Quadtree Diffusion Model (QDM), a region-adaptive diffusion framework that leverages a quadtree structure to selectively enhance detail-rich regions while reducing computations in homogeneous areas. By guiding the diffusion with a quadtree derived from the low-quality input, QDM identifies key regions-represented by leaf nodes-where fine detail is essential and applies minimal refinement elsewhere. This mask-guided, two-stream architecture adaptively balances quality and efficiency, producing high-fidelity outputs with low computational redundancy. Experiments demonstrate QDM's effectiveness in high-resolution SR tasks across diverse image types, particularly in medical imaging (e.g., CT scans), where large homogeneous regions are prevalent. Furthermore, QDM outperforms or is comparable to state-of-the-art SR methods on standard benchmarks while significantly reducing computational costs, highlighting its efficiency and suitability for resource-limited environments. Our code is available at https://github.com/linYDTHU/QDM.
Focus-N-Fix: Region-Aware Fine-Tuning for Text-to-Image Generation
Jan 11, 2025

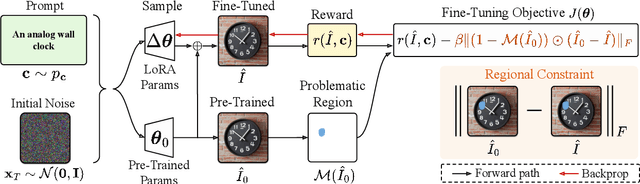
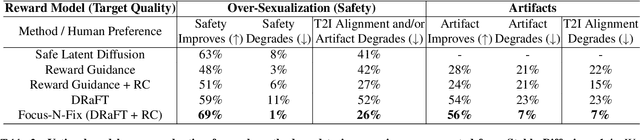
Abstract:Text-to-image (T2I) generation has made significant advances in recent years, but challenges still remain in the generation of perceptual artifacts, misalignment with complex prompts, and safety. The prevailing approach to address these issues involves collecting human feedback on generated images, training reward models to estimate human feedback, and then fine-tuning T2I models based on the reward models to align them with human preferences. However, while existing reward fine-tuning methods can produce images with higher rewards, they may change model behavior in unexpected ways. For example, fine-tuning for one quality aspect (e.g., safety) may degrade other aspects (e.g., prompt alignment), or may lead to reward hacking (e.g., finding a way to increase rewards without having the intended effect). In this paper, we propose Focus-N-Fix, a region-aware fine-tuning method that trains models to correct only previously problematic image regions. The resulting fine-tuned model generates images with the same high-level structure as the original model but shows significant improvements in regions where the original model was deficient in safety (over-sexualization and violence), plausibility, or other criteria. Our experiments demonstrate that Focus-N-Fix improves these localized quality aspects with little or no degradation to others and typically imperceptible changes in the rest of the image. Disclaimer: This paper contains images that may be overly sexual, violent, offensive, or harmful.
Directly Fine-Tuning Diffusion Models on Differentiable Rewards
Sep 29, 2023



Abstract:We present Direct Reward Fine-Tuning (DRaFT), a simple and effective method for fine-tuning diffusion models to maximize differentiable reward functions, such as scores from human preference models. We first show that it is possible to backpropagate the reward function gradient through the full sampling procedure, and that doing so achieves strong performance on a variety of rewards, outperforming reinforcement learning-based approaches. We then propose more efficient variants of DRaFT: DRaFT-K, which truncates backpropagation to only the last K steps of sampling, and DRaFT-LV, which obtains lower-variance gradient estimates for the case when K=1. We show that our methods work well for a variety of reward functions and can be used to substantially improve the aesthetic quality of images generated by Stable Diffusion 1.4. Finally, we draw connections between our approach and prior work, providing a unifying perspective on the design space of gradient-based fine-tuning algorithms.
Low-Variance Gradient Estimation in Unrolled Computation Graphs with ES-Single
Apr 21, 2023

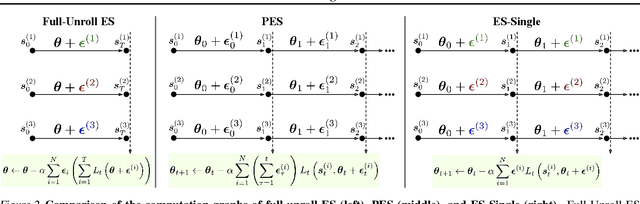

Abstract:We propose an evolution strategies-based algorithm for estimating gradients in unrolled computation graphs, called ES-Single. Similarly to the recently-proposed Persistent Evolution Strategies (PES), ES-Single is unbiased, and overcomes chaos arising from recursive function applications by smoothing the meta-loss landscape. ES-Single samples a single perturbation per particle, that is kept fixed over the course of an inner problem (e.g., perturbations are not re-sampled for each partial unroll). Compared to PES, ES-Single is simpler to implement and has lower variance: the variance of ES-Single is constant with respect to the number of truncated unrolls, removing a key barrier in applying ES to long inner problems using short truncations. We show that ES-Single is unbiased for quadratic inner problems, and demonstrate empirically that its variance can be substantially lower than that of PES. ES-Single consistently outperforms PES on a variety of tasks, including a synthetic benchmark task, hyperparameter optimization, training recurrent neural networks, and training learned optimizers.
On Implicit Bias in Overparameterized Bilevel Optimization
Dec 28, 2022Abstract:Many problems in machine learning involve bilevel optimization (BLO), including hyperparameter optimization, meta-learning, and dataset distillation. Bilevel problems consist of two nested sub-problems, called the outer and inner problems, respectively. In practice, often at least one of these sub-problems is overparameterized. In this case, there are many ways to choose among optima that achieve equivalent objective values. Inspired by recent studies of the implicit bias induced by optimization algorithms in single-level optimization, we investigate the implicit bias of gradient-based algorithms for bilevel optimization. We delineate two standard BLO methods -- cold-start and warm-start -- and show that the converged solution or long-run behavior depends to a large degree on these and other algorithmic choices, such as the hypergradient approximation. We also show that the inner solutions obtained by warm-start BLO can encode a surprising amount of information about the outer objective, even when the outer parameters are low-dimensional. We believe that implicit bias deserves as central a role in the study of bilevel optimization as it has attained in the study of single-level neural net optimization.
Beyond the Imitation Game: Quantifying and extrapolating the capabilities of language models
Jun 10, 2022Abstract:Language models demonstrate both quantitative improvement and new qualitative capabilities with increasing scale. Despite their potentially transformative impact, these new capabilities are as yet poorly characterized. In order to inform future research, prepare for disruptive new model capabilities, and ameliorate socially harmful effects, it is vital that we understand the present and near-future capabilities and limitations of language models. To address this challenge, we introduce the Beyond the Imitation Game benchmark (BIG-bench). BIG-bench currently consists of 204 tasks, contributed by 442 authors across 132 institutions. Task topics are diverse, drawing problems from linguistics, childhood development, math, common-sense reasoning, biology, physics, social bias, software development, and beyond. BIG-bench focuses on tasks that are believed to be beyond the capabilities of current language models. We evaluate the behavior of OpenAI's GPT models, Google-internal dense transformer architectures, and Switch-style sparse transformers on BIG-bench, across model sizes spanning millions to hundreds of billions of parameters. In addition, a team of human expert raters performed all tasks in order to provide a strong baseline. Findings include: model performance and calibration both improve with scale, but are poor in absolute terms (and when compared with rater performance); performance is remarkably similar across model classes, though with benefits from sparsity; tasks that improve gradually and predictably commonly involve a large knowledge or memorization component, whereas tasks that exhibit "breakthrough" behavior at a critical scale often involve multiple steps or components, or brittle metrics; social bias typically increases with scale in settings with ambiguous context, but this can be improved with prompting.
Amortized Proximal Optimization
Feb 28, 2022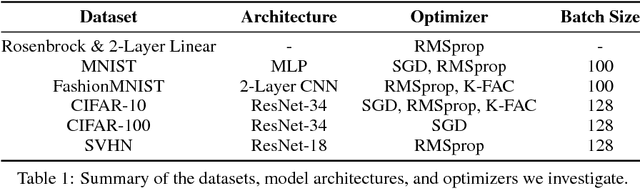
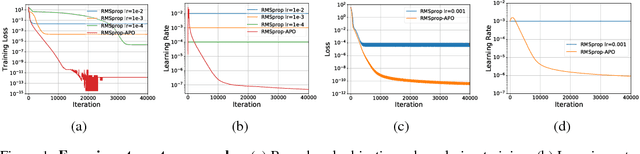
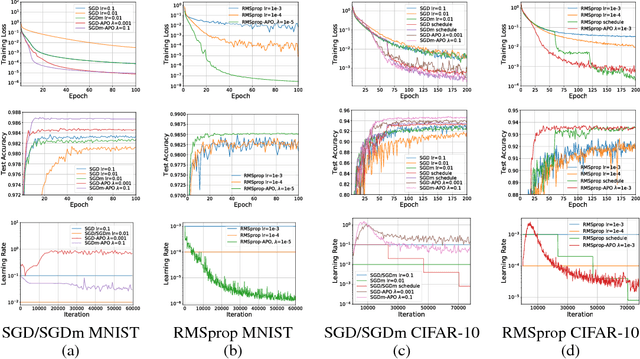

Abstract:We propose a framework for online meta-optimization of parameters that govern optimization, called Amortized Proximal Optimization (APO). We first interpret various existing neural network optimizers as approximate stochastic proximal point methods which trade off the current-batch loss with proximity terms in both function space and weight space. The idea behind APO is to amortize the minimization of the proximal point objective by meta-learning the parameters of an update rule. We show how APO can be used to adapt a learning rate or a structured preconditioning matrix. Under appropriate assumptions, APO can recover existing optimizers such as natural gradient descent and KFAC. It enjoys low computational overhead and avoids expensive and numerically sensitive operations required by some second-order optimizers, such as matrix inverses. We empirically test APO for online adaptation of learning rates and structured preconditioning matrices for regression, image reconstruction, image classification, and natural language translation tasks. Empirically, the learning rate schedules found by APO generally outperform optimal fixed learning rates and are competitive with manually tuned decay schedules. Using APO to adapt a structured preconditioning matrix generally results in optimization performance competitive with second-order methods. Moreover, the absence of matrix inversion provides numerical stability, making it effective for low precision training.
Disentanglement and Generalization Under Correlation Shifts
Dec 29, 2021



Abstract:Correlations between factors of variation are prevalent in real-world data. Machine learning algorithms may benefit from exploiting such correlations, as they can increase predictive performance on noisy data. However, often such correlations are not robust (e.g., they may change between domains, datasets, or applications) and we wish to avoid exploiting them. Disentanglement methods aim to learn representations which capture different factors of variation in latent subspaces. A common approach involves minimizing the mutual information between latent subspaces, such that each encodes a single underlying attribute. However, this fails when attributes are correlated. We solve this problem by enforcing independence between subspaces conditioned on the available attributes, which allows us to remove only dependencies that are not due to the correlation structure present in the training data. We achieve this via an adversarial approach to minimize the conditional mutual information (CMI) between subspaces with respect to categorical variables. We first show theoretically that CMI minimization is a good objective for robust disentanglement on linear problems with Gaussian data. We then apply our method on real-world datasets based on MNIST and CelebA, and show that it yields models that are disentangled and robust under correlation shift, including in weakly supervised settings.
Unbiased Gradient Estimation in Unrolled Computation Graphs with Persistent Evolution Strategies
Dec 27, 2021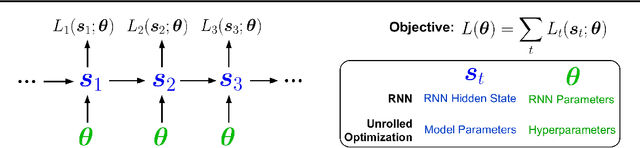
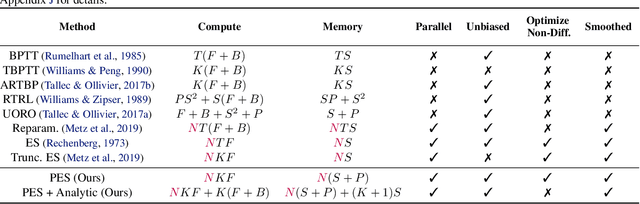
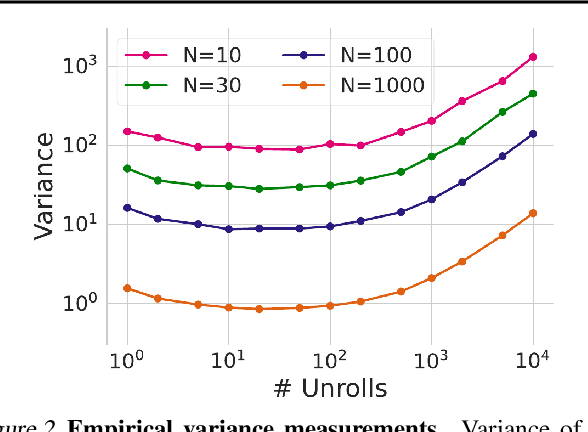

Abstract:Unrolled computation graphs arise in many scenarios, including training RNNs, tuning hyperparameters through unrolled optimization, and training learned optimizers. Current approaches to optimizing parameters in such computation graphs suffer from high variance gradients, bias, slow updates, or large memory usage. We introduce a method called Persistent Evolution Strategies (PES), which divides the computation graph into a series of truncated unrolls, and performs an evolution strategies-based update step after each unroll. PES eliminates bias from these truncations by accumulating correction terms over the entire sequence of unrolls. PES allows for rapid parameter updates, has low memory usage, is unbiased, and has reasonable variance characteristics. We experimentally demonstrate the advantages of PES compared to several other methods for gradient estimation on synthetic tasks, and show its applicability to training learned optimizers and tuning hyperparameters.
Lyapunov Exponents for Diversity in Differentiable Games
Dec 24, 2021


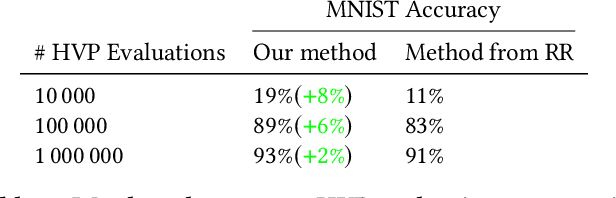
Abstract:Ridge Rider (RR) is an algorithm for finding diverse solutions to optimization problems by following eigenvectors of the Hessian ("ridges"). RR is designed for conservative gradient systems (i.e., settings involving a single loss function), where it branches at saddles - easy-to-find bifurcation points. We generalize this idea to non-conservative, multi-agent gradient systems by proposing a method - denoted Generalized Ridge Rider (GRR) - for finding arbitrary bifurcation points. We give theoretical motivation for our method by leveraging machinery from the field of dynamical systems. We construct novel toy problems where we can visualize new phenomena while giving insight into high-dimensional problems of interest. Finally, we empirically evaluate our method by finding diverse solutions in the iterated prisoners' dilemma and relevant machine learning problems including generative adversarial networks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge