David vs. Goliath: Verifiable Agent-to-Agent Jailbreaking via Reinforcement Learning

The evolution of large language models into autonomous agents introduces adversarial failures that exploit legitimate tool privileges, transforming safety evaluation in tool-augmented environments from a subjective NLP task into an objective control problem. We formalize this threat model as Tag-Along Attacks: a scenario where a tool-less adversary "tags along" on the trusted privileges of a safety-aligned Operator to induce prohibited tool use through conversation alone. To validate this threat, we present Slingshot, a 'cold-start' reinforcement learning framework that autonomously discovers emergent attack vectors, revealing a critical insight: in our setting, learned attacks tend to converge to short, instruction-like syntactic patterns rather than multi-turn persuasion. On held-out extreme-difficulty tasks, Slingshot achieves a 67.0% success rate against a Qwen2.5-32B-Instruct-AWQ Operator (vs. 1.7% baseline), reducing the expected attempts to first success (on solved tasks) from 52.3 to 1.3. Crucially, Slingshot transfers zero-shot to several model families, including closed-source models like Gemini 2.5 Flash (56.0% attack success rate) and defensive-fine-tuned open-source models like Meta-SecAlign-8B (39.2% attack success rate). Our work establishes Tag-Along Attacks as a first-class, verifiable threat model and shows that effective agentic attacks can be elicited from off-the-shelf open-weight models through environment interaction alone.

Modelling Mean-Field Games with Neural Ordinary Differential Equations

Mean-field game theory relies on approximating games that would otherwise have been intractable to model. While the games can be solved analytically via the associated system of partial derivatives, this approach is not model-free, can lead to the loss of the existence or uniqueness of solutions and may suffer from modelling bias. To reduce the dependency between the model and the game, we combine mean-field game theory with deep learning in the form of neural ordinary differential equations. The resulting model is data-driven, lightweight and can learn extensive strategic interactions that are hard to capture using mean-field theory alone. In addition, the model is based on automatic differentiation, making it more robust and objective than approaches based on finite differences. We highlight the efficiency and flexibility of our approach by solving three mean-field games that vary in their complexity, observability and the presence of noise. Using these results, we show that the model is flexible, lightweight and requires few observations to learn the distribution underlying the data.

InfluenceNet: AI Models for Banzhaf and Shapley Value Prediction

Power indices are essential in assessing the contribution and influence of individual agents in multi-agent systems, providing crucial insights into collaborative dynamics and decision-making processes. While invaluable, traditional computational methods for exact or estimated power indices values require significant time and computational constraints, especially for large $(n\ge10)$ coalitions. These constraints have historically limited researchers' ability to analyse complex multi-agent interactions comprehensively. To address this limitation, we introduce a novel Neural Networks-based approach that efficiently estimates power indices for voting games, demonstrating comparable and often superiour performance to existing tools in terms of both speed and accuracy. This method not only addresses existing computational bottlenecks, but also enables rapid analysis of large coalitions, opening new avenues for multi-agent system research by overcoming previous computational limitations and providing researchers with a more accessible, scalable analytical tool.This increased efficiency will allow for the analysis of more complex and realistic multi-agent scenarios.

Using Cooperative Game Theory to Prune Neural Networks

We show how solution concepts from cooperative game theory can be used to tackle the problem of pruning neural networks. The ever-growing size of deep neural networks (DNNs) increases their performance, but also their computational requirements. We introduce a method called Game Theory Assisted Pruning (GTAP), which reduces the neural network's size while preserving its predictive accuracy. GTAP is based on eliminating neurons in the network based on an estimation of their joint impact on the prediction quality through game theoretic solutions. Specifically, we use a power index akin to the Shapley value or Banzhaf index, tailored using a procedure similar to Dropout (commonly used to tackle overfitting problems in machine learning). Empirical evaluation of both feedforward networks and convolutional neural networks shows that this method outperforms existing approaches in the achieved tradeoff between the number of parameters and model accuracy.

Generating and Imputing Tabular Data via Diffusion and Flow-based Gradient-Boosted Trees

Tabular data is hard to acquire and is subject to missing values. This paper proposes a novel approach to generate and impute mixed-type (continuous and categorical) tabular data using score-based diffusion and conditional flow matching. Contrary to previous work that relies on neural networks as function approximators, we instead utilize XGBoost, a popular Gradient-Boosted Tree (GBT) method. In addition to being elegant, we empirically show on various datasets that our method i) generates highly realistic synthetic data when the training dataset is either clean or tainted by missing data and ii) generates diverse plausible data imputations. Our method often outperforms deep-learning generation methods and can trained in parallel using CPUs without the need for a GPU. To make it easily accessible, we release our code through a Python library on PyPI and an R package on CRAN.

Explainability Techniques for Chemical Language Models

Explainability techniques are crucial in gaining insights into the reasons behind the predictions of deep learning models, which have not yet been applied to chemical language models. We propose an explainable AI technique that attributes the importance of individual atoms towards the predictions made by these models. Our method backpropagates the relevance information towards the chemical input string and visualizes the importance of individual atoms. We focus on self-attention Transformers operating on molecular string representations and leverage a pretrained encoder for finetuning. We showcase the method by predicting and visualizing solubility in water and organic solvents. We achieve competitive model performance while obtaining interpretable predictions, which we use to inspect the pretrained model.

Charting the Topography of the Neural Network Landscape with Thermal-Like Noise

The training of neural networks is a complex, high-dimensional, non-convex and noisy optimization problem whose theoretical understanding is interesting both from an applicative perspective and for fundamental reasons. A core challenge is to understand the geometry and topography of the landscape that guides the optimization. In this work, we employ standard Statistical Mechanics methods, namely, phase-space exploration using Langevin dynamics, to study this landscape for an over-parameterized fully connected network performing a classification task on random data. Analyzing the fluctuation statistics, in analogy to thermal dynamics at a constant temperature, we infer a clear geometric description of the low-loss region. We find that it is a low-dimensional manifold whose dimension can be readily obtained from the fluctuations. Furthermore, this dimension is controlled by the number of data points that reside near the classification decision boundary. Importantly, we find that a quadratic approximation of the loss near the minimum is fundamentally inadequate due to the exponential nature of the decision boundary and the flatness of the low-loss region. This causes the dynamics to sample regions with higher curvature at higher temperatures, while producing quadratic-like statistics at any given temperature. We explain this behavior by a simplified loss model which is analytically tractable and reproduces the observed fluctuation statistics.

Diffusion models with location-scale noise

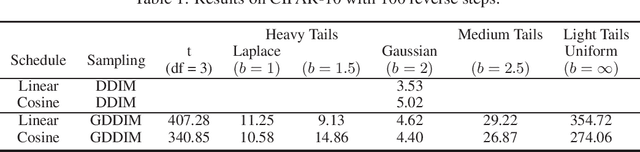
Diffusion Models (DMs) are powerful generative models that add Gaussian noise to the data and learn to remove it. We wanted to determine which noise distribution (Gaussian or non-Gaussian) led to better generated data in DMs. Since DMs do not work by design with non-Gaussian noise, we built a framework that allows reversing a diffusion process with non-Gaussian location-scale noise. We use that framework to show that the Gaussian distribution performs the best over a wide range of other distributions (Laplace, Uniform, t, Generalized-Gaussian).

Safe Reinforcement Learning From Pixels Using a Stochastic Latent Representation

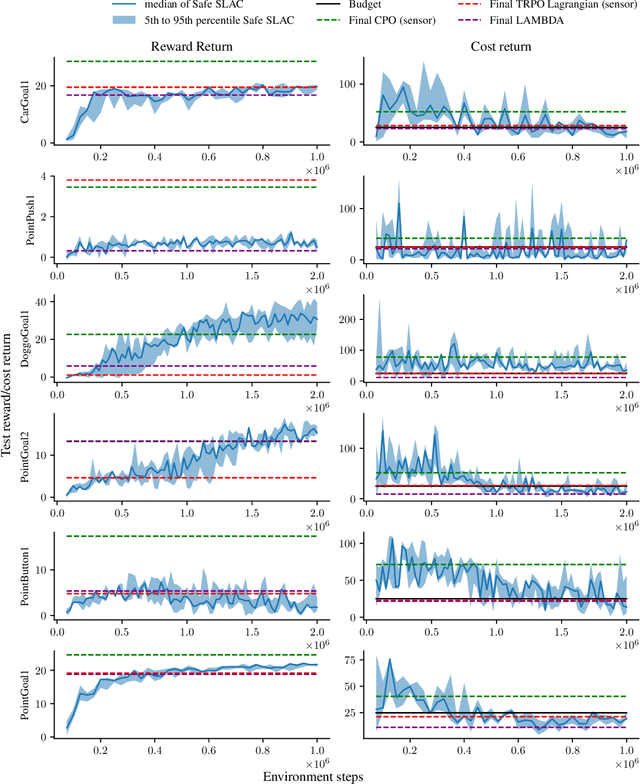
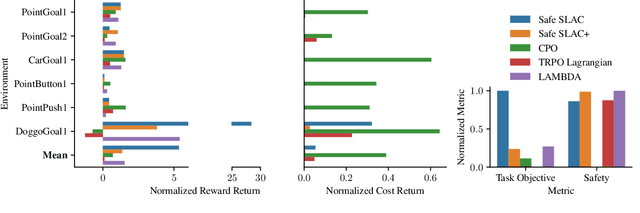
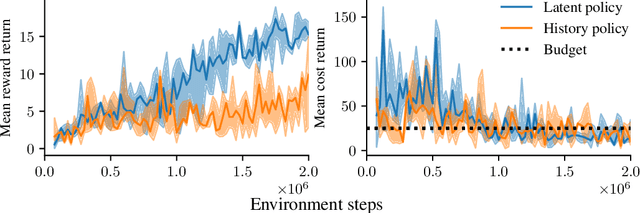
We address the problem of safe reinforcement learning from pixel observations. Inherent challenges in such settings are (1) a trade-off between reward optimization and adhering to safety constraints, (2) partial observability, and (3) high-dimensional observations. We formalize the problem in a constrained, partially observable Markov decision process framework, where an agent obtains distinct reward and safety signals. To address the curse of dimensionality, we employ a novel safety critic using the stochastic latent actor-critic (SLAC) approach. The latent variable model predicts rewards and safety violations, and we use the safety critic to train safe policies. Using well-known benchmark environments, we demonstrate competitive performance over existing approaches with respects to computational requirements, final reward return, and satisfying the safety constraints.

Neural Payoff Machines: Predicting Fair and Stable Payoff Allocations Among Team Members

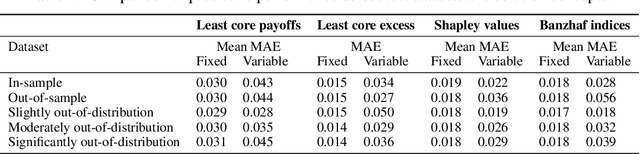
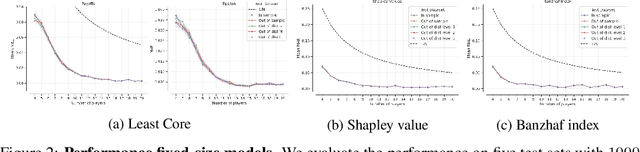
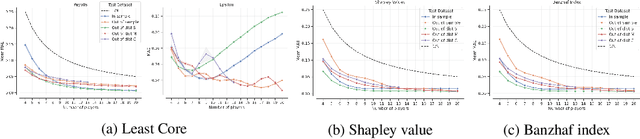
In many multi-agent settings, participants can form teams to achieve collective outcomes that may far surpass their individual capabilities. Measuring the relative contributions of agents and allocating them shares of the reward that promote long-lasting cooperation are difficult tasks. Cooperative game theory offers solution concepts identifying distribution schemes, such as the Shapley value, that fairly reflect the contribution of individuals to the performance of the team or the Core, which reduces the incentive of agents to abandon their team. Applications of such methods include identifying influential features and sharing the costs of joint ventures or team formation. Unfortunately, using these solutions requires tackling a computational barrier as they are hard to compute, even in restricted settings. In this work, we show how cooperative game-theoretic solutions can be distilled into a learned model by training neural networks to propose fair and stable payoff allocations. We show that our approach creates models that can generalize to games far from the training distribution and can predict solutions for more players than observed during training. An important application of our framework is Explainable AI: our approach can be used to speed-up Shapley value computations on many instances.