Communication trade-offs for synchronized distributed SGD with large step size
Paper and Code
Apr 25, 2019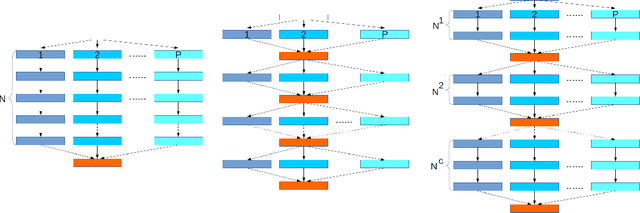

Synchronous mini-batch SGD is state-of-the-art for large-scale distributed machine learning. However, in practice, its convergence is bottlenecked by slow communication rounds between worker nodes. A natural solution to reduce communication is to use the \emph{`local-SGD'} model in which the workers train their model independently and synchronize every once in a while. This algorithm improves the computation-communication trade-off but its convergence is not understood very well. We propose a non-asymptotic error analysis, which enables comparison to \emph{one-shot averaging} i.e., a single communication round among independent workers, and \emph{mini-batch averaging} i.e., communicating at every step. We also provide adaptive lower bounds on the communication frequency for large step-sizes ($ t^{-\alpha} $, $ \alpha\in (1/2 , 1 ) $) and show that \emph{Local-SGD} reduces communication by a factor of $O\Big(\frac{\sqrt{T}}{P^{3/2}}\Big)$, with $T$ the total number of gradients and $P$ machines.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge