SANNS: Scaling Up Secure Approximate k-Nearest Neighbors Search

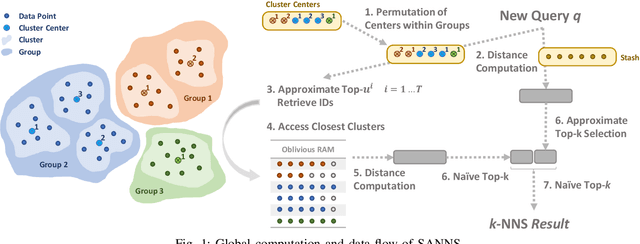
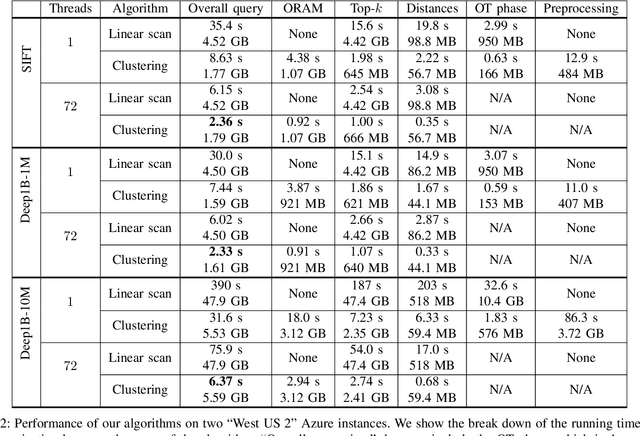
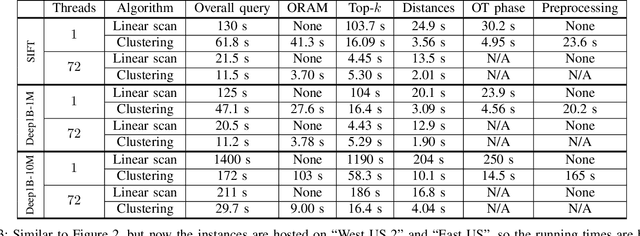
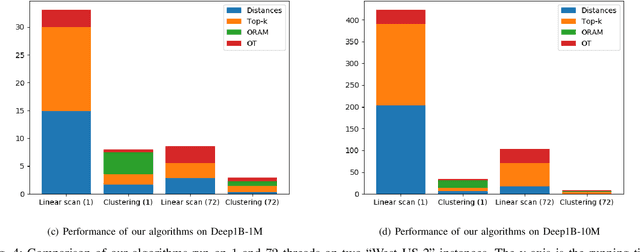
We present new secure protocols for approximate $k$-nearest neighbor search ($k$-NNS) over the Euclidean distance in the semi-honest model. Our implementation is able to handle massive datasets efficiently. On the algorithmic front, we show a new circuit for the approximate top-$k$ selection from $n$ numbers that is built from merely $O(n + \mathrm{poly}(k))$ comparators. Using this circuit as a subroutine, we design new approximate $k$-NNS algorithms and two corresponding secure protocols: 1) optimized linear scan; 2) clustering-based sublinear time algorithm. Our secure protocols utilize a combination of additively-homomorphic encryption, garbled circuit and Oblivious RAM. Along the way, we introduce various optimizations to these primitives, which drastically improve concrete efficiency. We evaluate the new protocols empirically and show that they are able to handle datasets that are significantly larger than in the prior work. For instance, running on two standard Azure instances within the same availability zone, for a dataset of $96$-dimensional descriptors of $10\,000\,000$ images, we can find $10$ nearest neighbors with average accuracy $0.9$ in under $10$ seconds improving upon prior work by at least two orders of magnitude.