Physics-constrained DeepONet for Surrogate CFD models: a curved backward-facing step case

The Physics-Constrained DeepONet (PC-DeepONet), an architecture that incorporates fundamental physics knowledge into the data-driven DeepONet model, is presented in this study. This methodology is exemplified through surrogate modeling of fluid dynamics over a curved backward-facing step, a benchmark problem in computational fluid dynamics. The model was trained on computational fluid dynamics data generated for a range of parameterized geometries. The PC-DeepONet was able to learn the mapping from the parameters describing the geometry to the velocity and pressure fields. While the DeepONet is solely data-driven, the PC-DeepONet imposes the divergence constraint from the continuity equation onto the network. The PC-DeepONet demonstrates higher accuracy than the data-driven baseline, especially when trained on sparse data. Both models attain convergence with a small dataset of 50 samples and require only 50 iterations for convergence, highlighting the efficiency of neural operators in learning the dynamics governed by partial differential equations.

Exploring GPU-to-GPU Communication: Insights into Supercomputer Interconnects

Multi-GPU nodes are increasingly common in the rapidly evolving landscape of exascale supercomputers. On these systems, GPUs on the same node are connected through dedicated networks, with bandwidths up to a few terabits per second. However, gauging performance expectations and maximizing system efficiency is challenging due to different technologies, design options, and software layers. This paper comprehensively characterizes three supercomputers - Alps, Leonardo, and LUMI - each with a unique architecture and design. We focus on performance evaluation of intra-node and inter-node interconnects on up to 4096 GPUs, using a mix of intra-node and inter-node benchmarks. By analyzing its limitations and opportunities, we aim to offer practical guidance to researchers, system architects, and software developers dealing with multi-GPU supercomputing. Our results show that there is untapped bandwidth, and there are still many opportunities for optimization, ranging from network to software optimization.

Towards a learning-based performance modeling for accelerating Deep Neural Networks

Emerging applications such as Deep Learning are often data-driven, thus traditional approaches based on auto-tuners are not performance effective across the wide range of inputs used in practice. In the present paper, we start an investigation of predictive models based on machine learning techniques in order to optimize Convolution Neural Networks (CNNs). As a use-case, we focus on the ARM Compute Library which provides three different implementations of the convolution operator at different numeric precision. Starting from a collation of benchmarks, we build and validate models learned by Decision Tree and naive Bayesian classifier. Preliminary experiments on Midgard-based ARM Mali GPU show that our predictive model outperforms all the convolution operators manually selected by the library.

GPU-based parallelism for ASP-solving

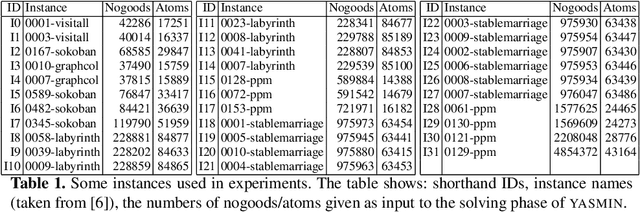
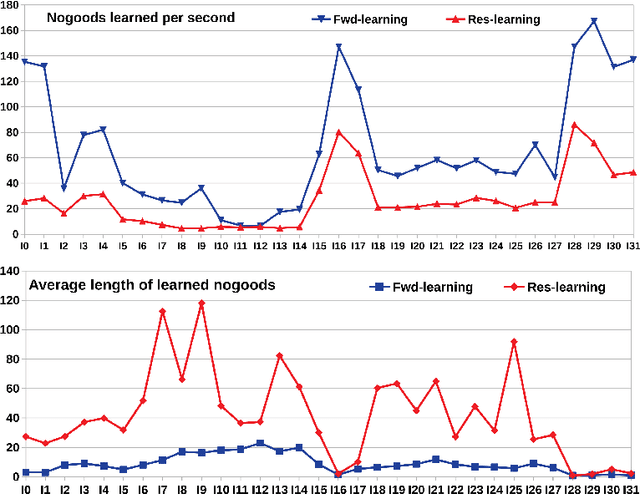
Answer Set Programming (ASP) has become, the paradigm of choice in the field of logic programming and non-monotonic reasoning. Thanks to the availability of efficient solvers, ASP has been successfully employed in a large number of application domains. The term GPU-computing indicates a recent programming paradigm aimed at enabling the use of modern parallel Graphical Processing Units (GPUs) for general purpose computing. In this paper we describe an approach to ASP-solving that exploits GPU parallelism. The design of a GPU-based solver poses various challenges due to the peculiarities of GPUs' software and hardware architectures and to the intrinsic nature of the satisfiability problem.

A Computational Model for Tensor Core Units

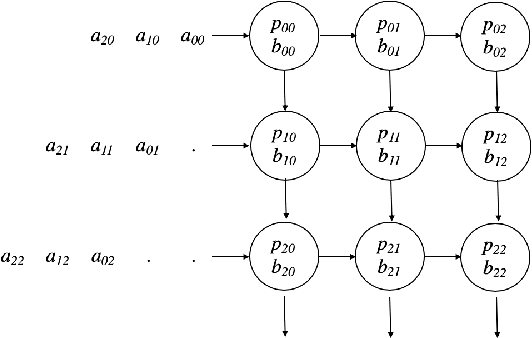
To respond to the need of efficient training and inference of deep neural networks, a pletora of domain-specific hardware architectures have been introduced, such as Google Tensor Processing Units and NVIDIA Tensor Cores. A common feature of these architectures is a hardware circuit for efficiently computing a dense matrix multiplication of a given small size. In order to broad the class of algorithms that exploit these systems, we propose a computational model, named TCU model, that captures the ability to natively multiply small matrices. We then use the TCU model for designing fast algorithms for linear algebra problems, including dense and sparse matrix multiplication, FFT, integer multiplication, and polynomial evaluation. We finally highlight a relation between the TCU model and the external memory model.