Quick Heuristic Validation of Edges in Dynamic Roadmap Graphs

In this paper we tackle the problem of adjusting roadmap graphs for robot motion planning to non-static environments. We introduce the "Red-Green-Gray" paradigm, a modification of the SPITE method, capable of classifying the validity status of nodes and edges using cheap heuristic checks, allowing fast semi-lazy roadmap updates. Given a roadmap, we use simple computational geometry methods to approximate the swept volumes of robots and perform lazy collision checks, and label a subset of the edges as invalid (red), valid (green), or unknown (gray). We present preliminary experimental results comparing our method to the well-established technique of Leven and Hutchinson, and showing increased accuracy as well as the ability to correctly label edges as invalid while maintaining comparable update runtimes.

Faster Motion Planning via Restarts

Randomized methods such as PRM and RRT are widely used in motion planning. However, in some cases, their running-time suffers from inherent instability, leading to ``catastrophic'' performance even for relatively simple instances. We apply stochastic restart techniques, some of them new, for speeding up Las Vegas algorithms, that provide dramatic speedups in practice (a factor of $3$ [or larger] in many cases). Our experiments demonstrate that the new algorithms have faster runtimes, shorter paths, and greater gains from multi-threading (when compared with straightforward parallel implementation). We prove the optimality of the new variants. Our implementation is open source, available on github, and is easy to deploy and use.

Edge Nearest Neighbor in Sampling-Based Motion Planning

Neighborhood finders and nearest neighbor queries are fundamental parts of sampling based motion planning algorithms. Using different distance metrics or otherwise changing the definition of a neighborhood produces different algorithms with unique empiric and theoretical properties. In \cite{l-pa-06} LaValle suggests a neighborhood finder for the Rapidly-exploring Random Tree RRT algorithm \cite{l-rrtnt-98} which finds the nearest neighbor of the sampled point on the swath of the tree, that is on the set of all of the points on the tree edges, using a hierarchical data structure. In this paper we implement such a neighborhood finder and show, theoretically and experimentally, that this results in more efficient algorithms, and suggest a variant of the Rapidly-exploring Random Graph RRG algorithm \cite{f-isaom-10} that better exploits the exploration properties of the newly described subroutine for finding narrow passages.

SPITE: Simple Polyhedral Intersection Techniques for modified Environments

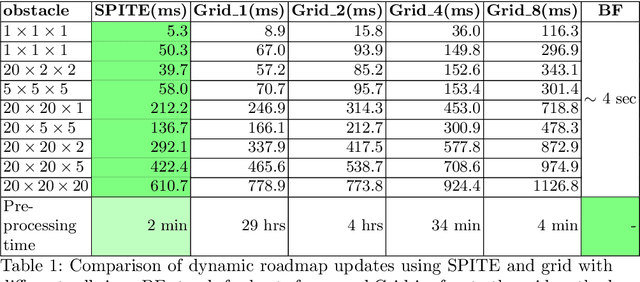
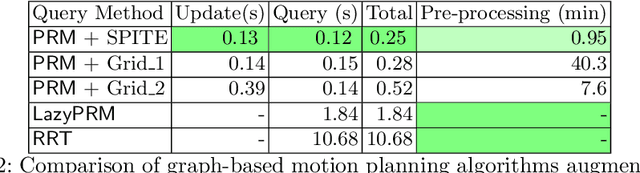
Motion planning in modified environments is a challenging task, as it compounds the innate difficulty of the motion planning problem with a changing environment. This renders some algorithmic methods such as probabilistic roadmaps less viable, as nodes and edges may become invalid as a result of these changes. In this paper, we present a method of transforming any configuration space graph, such as a roadmap, to a dynamic data structure capable of updating the validity of its nodes and edges in response to discrete changes in obstacle positions. We use methods from computational geometry to compute 3D swept volume approximations of configuration space points and curves to achieve 10-40 percent faster updates and up to 60 percent faster motion planning queries than previous algorithms while requiring a significantly shorter pre-processing phase, requiring minutes instead of hours needed by the competing method to achieve somewhat similar update times.

A Framework for Guided Motion Planning

Randomized sampling based algorithms are widely used in robot motion planning due to the problem's intractability, and are experimentally effective on a wide range of problem instances. Most variants bias their sampling using various heuristics related to the known underlying structure of the search space. In this work, we formalize the intuitive notion of guided search by defining the concept of a guiding space. This new language encapsulates many seemingly distinct prior methods under the same framework, and allows us to reason about guidance, a previously obscured core contribution of different algorithms. We suggest an information theoretic method to evaluate guidance, which experimentally matches intuition when tested on known algorithms in a variety of environments. The language and evaluation of guidance suggests improvements to existing methods, and allows for simple hybrid algorithms that combine guidance from multiple sources.

Evaluating Guiding Spaces for Motion Planning

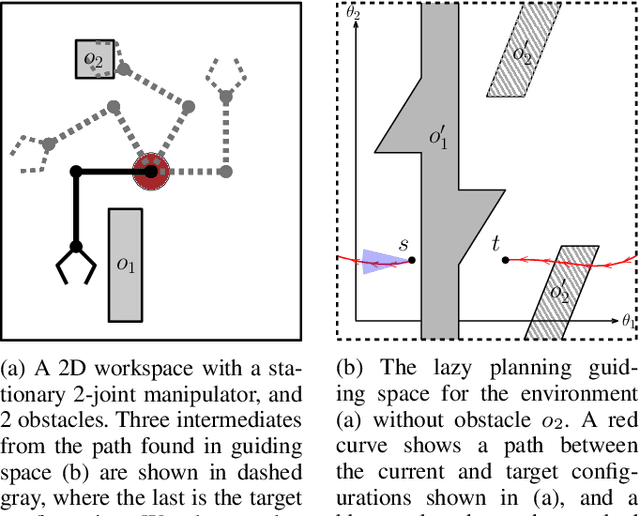
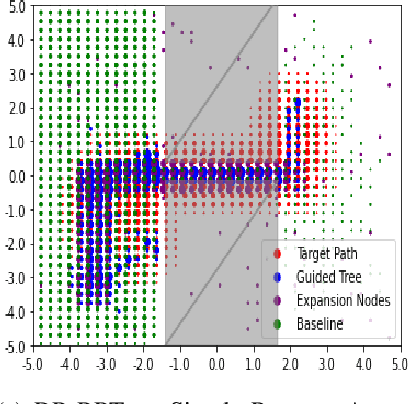
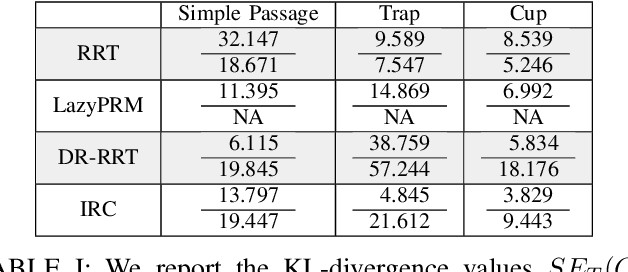
Randomized sampling based algorithms are widely used in robot motion planning due to the problem's intractability, and are experimentally effective on a wide range of problem instances. Most variants do not sample uniformly at random, and instead bias their sampling using various heuristics for determining which samples will provide more information, or are more likely to participate in the final solution. In this work, we define the \emph{motion planning guiding space}, which encapsulates many seemingly distinct prior works under the same framework. In addition, we suggest an information theoretic method to evaluate guided planning which places the focus on the quality of the resulting biased sampling. Finally, we analyze several motion planning algorithms in order to demonstrate the applicability of our definition and its evaluation.