Unlabeled Multi-Robot Motion Planning with Tighter Separation Bounds

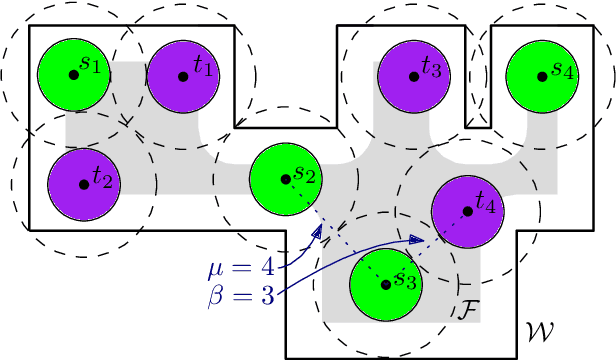
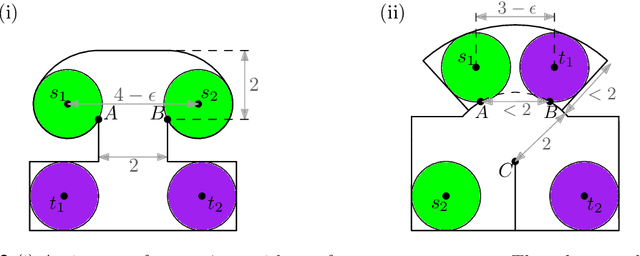
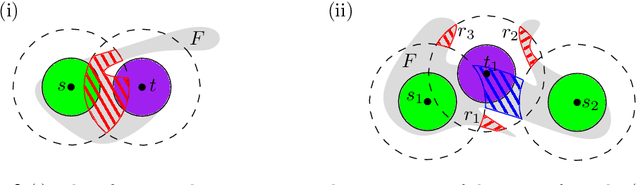
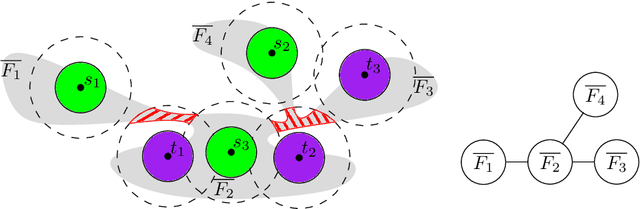
We consider the unlabeled motion-planning problem of $m$ unit-disc robots moving in a simple polygonal workspace of $n$ edges. The goal is to find a motion plan that moves the robots to a given set of $m$ target positions. For the unlabeled variant, it does not matter which robot reaches which target position as long as all target positions are occupied in the end. If the workspace has narrow passages such that the robots cannot fit through them, then the free configuration space, representing all possible unobstructed positions of the robots, will consist of multiple connected components. Even if in each component of the free space the number of targets matches the number of start positions, the motion-planning problem does not always have a solution when the robots and their targets are positioned very densely. In this paper, we prove tight bounds on how much separation between start and target positions is necessary to always guarantee a solution. Moreover, we describe an algorithm that always finds a solution in time $O(n \log n + mn + m^2)$ if the separation bounds are met. Specifically, we prove that the following separation is sufficient: any two start positions are at least distance $4$ apart, any two target positions are at least distance $4$ apart, and any pair of a start and a target positions is at least distance $3$ apart. We further show that when the free space consists of a single connected component, the separation between start and target positions is not necessary.

Impossibility Results for Grammar-Compressed Linear Algebra

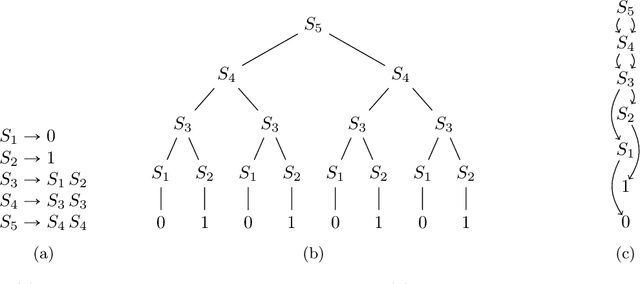
To handle vast amounts of data, it is natural and popular to compress vectors and matrices. When we compress a vector from size $N$ down to size $n \ll N$, it certainly makes it easier to store and transmit efficiently, but does it also make it easier to process? In this paper we consider lossless compression schemes, and ask if we can run our computations on the compressed data as efficiently as if the original data was that small. That is, if an operation has time complexity $T(\rm{inputsize})$, can we perform it on the compressed representation in time $T(n)$ rather than $T(N)$? We consider the most basic linear algebra operations: inner product, matrix-vector multiplication, and matrix multiplication. In particular, given two compressed vectors, can we compute their inner product in time $O(n)$? Or perhaps we must decompress first and then multiply, spending $\Omega(N)$ time? The answer depends on the compression scheme. While for simple ones such as Run-Length-Encoding (RLE) the inner product can be done in $O(n)$ time, we prove that this is impossible for compressions from a richer class: essentially $n^2$ or even larger runtimes are needed in the worst case (under complexity assumptions). This is the class of grammar-compressions containing most popular methods such as the Lempel-Ziv family. These schemes are more compressing than the simple RLE, but alas, we prove that performing computations on them is much harder.

Approximation Algorithms for $\ell_0$-Low Rank Approximation

We study the $\ell_0$-Low Rank Approximation Problem, where the goal is, given an $m \times n$ matrix $A$, to output a rank-$k$ matrix $A'$ for which $\|A'-A\|_0$ is minimized. Here, for a matrix $B$, $\|B\|_0$ denotes the number of its non-zero entries. This NP-hard variant of low rank approximation is natural for problems with no underlying metric, and its goal is to minimize the number of disagreeing data positions. We provide approximation algorithms which significantly improve the running time and approximation factor of previous work. For $k > 1$, we show how to find, in poly$(mn)$ time for every $k$, a rank $O(k \log(n/k))$ matrix $A'$ for which $\|A'-A\|_0 \leq O(k^2 \log(n/k)) \mathrm{OPT}$. To the best of our knowledge, this is the first algorithm with provable guarantees for the $\ell_0$-Low Rank Approximation Problem for $k > 1$, even for bicriteria algorithms. For the well-studied case when $k = 1$, we give a $(2+\epsilon)$-approximation in {\it sublinear time}, which is impossible for other variants of low rank approximation such as for the Frobenius norm. We strengthen this for the well-studied case of binary matrices to obtain a $(1+O(\psi))$-approximation in sublinear time, where $\psi = \mathrm{OPT}/\lVert A\rVert_0$. For small $\psi$, our approximation factor is $1+o(1)$.

A PTAS for $\ell_p$-Low Rank Approximation

A number of recent works have studied algorithms for entrywise $\ell_p$-low rank approximation, namely algorithms which given an $n \times d$ matrix $A$ (with $n \geq d$), output a rank-$k$ matrix $B$ minimizing $\|A-B\|_p^p=\sum_{i,j} |A_{i,j} - B_{i,j}|^p$. We show the following: On the algorithmic side, for $p \in (0,2)$, we give the first $n^{\text{poly}(k/\epsilon)}$ time $(1+\epsilon)$-approximation algorithm. For $p = 0$, there are various problem formulations, a common one being the binary setting for which $A\in\{0,1\}^{n\times d}$ and $B = U \cdot V$, where $U\in\{0,1\}^{n \times k}$ and $V\in\{0,1\}^{k \times d}$. There are also various notions of multiplication $U \cdot V$, such as a matrix product over the reals, over a finite field, or over a Boolean semiring. We give the first PTAS for what we call the Generalized Binary $\ell_0$-Rank-$k$ Approximation problem, for which these variants are special cases. Our algorithm runs in time $(1/\epsilon)^{2^{O(k)}/\epsilon^{2}} \cdot nd \cdot \log^{2^k} d$. For the specific case of finite fields of constant size, we obtain an alternate algorithm with time $n \cdot d^{\text{poly}(k/\epsilon)}$. On the hardness front, for $p \in (1,2)$, we show under the Small Set Expansion Hypothesis and Exponential Time Hypothesis (ETH), there is no constant factor approximation algorithm running in time $2^{k^{\delta}}$ for a constant $\delta > 0$, showing an exponential dependence on $k$ is necessary. For $p = 0$, we observe that there is no approximation algorithm for the Generalized Binary $\ell_0$-Rank-$k$ Approximation problem running in time $2^{2^{\delta k}}$ for a constant $\delta > 0$. We also show for finite fields of constant size, under the ETH, that any fixed constant factor approximation algorithm requires $2^{k^{\delta}}$ time for a constant $\delta > 0$.

Approximating the volume of unions and intersections of high-dimensional geometric objects

We consider the computation of the volume of the union of high-dimensional geometric objects. While showing that this problem is #P-hard already for very simple bodies (i.e., axis-parallel boxes), we give a fast FPRAS for all objects where one can: (1) test whether a given point lies inside the object, (2) sample a point uniformly, (3) calculate the volume of the object in polynomial time. All three oracles can be weak, that is, just approximate. This implies that Klee's measure problem and the hypervolume indicator can be approximated efficiently even though they are #P-hard and hence cannot be solved exactly in time polynomial in the number of dimensions unless P=NP. Our algorithm also allows to approximate efficiently the volume of the union of convex bodies given by weak membership oracles. For the analogous problem of the intersection of high-dimensional geometric objects we prove #P-hardness for boxes and show that there is no multiplicative polynomial-time $2^{d^{1-\epsilon}}$-approximation for certain boxes unless NP=BPP, but give a simple additive polynomial-time $\epsilon$-approximation.