Efficient Multi-Robot Motion Planning for Unlabeled Discs in Simple Polygons

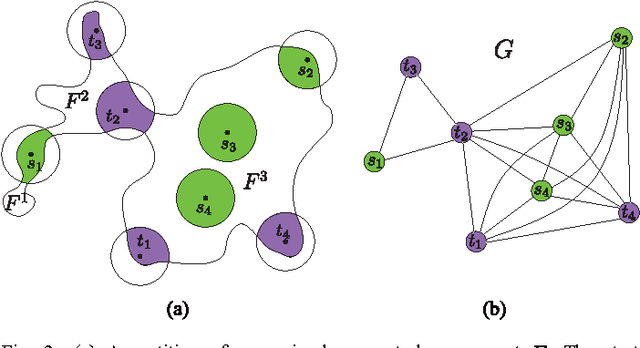
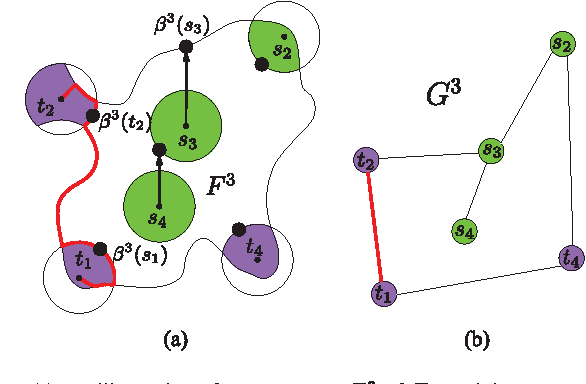
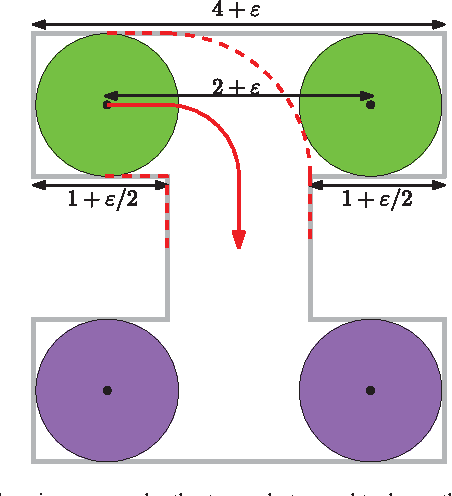
We consider the following motion-planning problem: we are given $m$ unit discs in a simple polygon with $n$ vertices, each at their own start position, and we want to move the discs to a given set of $m$ target positions. Contrary to the standard (labeled) version of the problem, each disc is allowed to be moved to any target position, as long as in the end every target position is occupied. We show that this unlabeled version of the problem can be solved in $O(n\log n+mn+m^2)$ time, assuming that the start and target positions are at least some minimal distance from each other. This is in sharp contrast to the standard (labeled) and more general multi-robot motion-planning problem for discs moving in a simple polygon, which is known to be strongly NP-hard.