Mobile Robot Localization Using a Novel Whisker-Like Sensor

Whisker-like touch sensors offer unique advantages for short-range perception in environments where visual and long-range sensing are unreliable, such as confined, cluttered, or low-visibility settings. This paper presents a framework for estimating contact points and robot localization in a known planar environment using a single whisker sensor. We develop a family of virtual sensor models. Each model maps robot configurations to sensor observations and enables structured reasoning through the concept of preimages - the set of robot states consistent with a given observation. The notion of virtual sensor models serves as an abstraction to reason about state uncertainty without dependence on physical implementation. By combining sensor observations with a motion model, we estimate the contact point. Iterative estimation then enables reconstruction of obstacle boundaries. Furthermore, intersecting states inferred from current observations with forward-projected states from previous steps allow accurate robot localization without relying on vision or external systems. The framework supports both deterministic and possibilistic formulations and is validated through simulation and physical experiments using a low-cost, 3D printed, Hall-effect-based whisker sensor. Results demonstrate accurate contact estimation and localization with errors under 7 mm, demonstrating the potential of whisker-based sensing as a lightweight, adaptable complement to vision-based navigation.

Optimal Control of Sensor-Induced Illusions on Robotic Agents

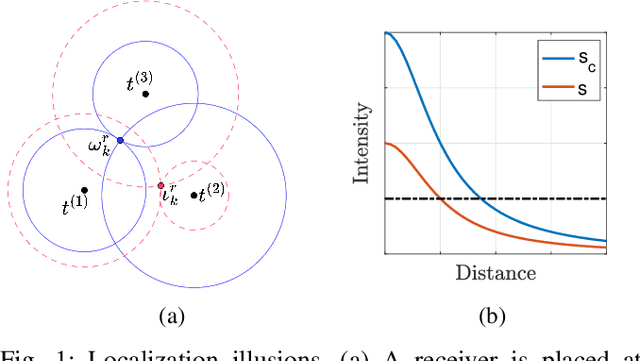
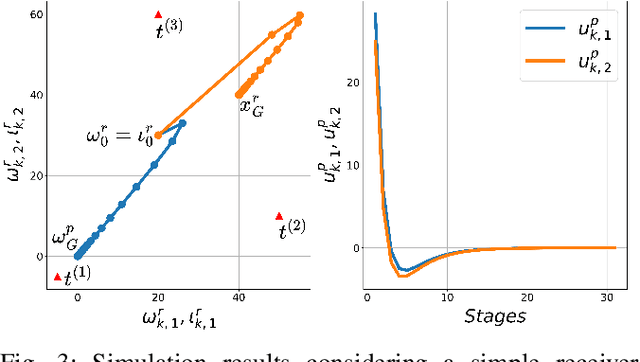
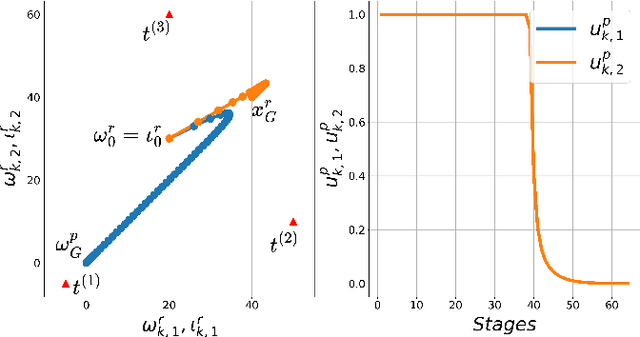
This paper presents a novel problem of creating and regulating localization and navigation illusions considering two agents: a receiver and a producer. A receiver is moving on a plane localizing itself using the intensity of signals from three known towers observed at its position. Based on this position estimate, it follows a simple policy to reach its goal. The key idea is that a producer alters the signal intensities to alter the position estimate of the receiver while ensuring it reaches a different destination with the belief that it reached its goal. We provide a precise mathematical formulation of this problem and show that it allows standard techniques from control theory to be applied to generate localization and navigation illusions that result in a desired receiver behavior.

Minimally sufficient structures for information-feedback policies

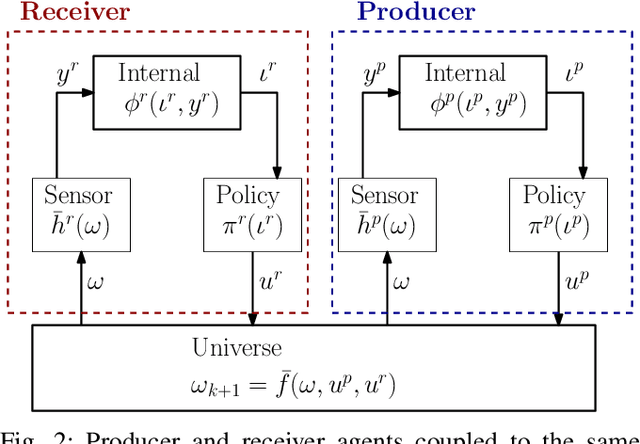
In this paper, we consider robotic tasks which require a desirable outcome to be achieved in the physical world that the robot is embedded in and interacting with. Accomplishing this objective requires designing a filter that maintains a useful representation of the physical world and a policy over the filter states. A filter is seen as the robot's perspective of the physical world based on limited sensing, memory, and computation and it is represented as a transition system over a space of information states. To this end, the interactions result from the coupling of an internal and an external system, a filter, and the physical world, respectively, through a sensor mapping and an information-feedback policy. Within this setup, we look for sufficient structures, that is, sufficient internal systems and sensors, for accomplishing a given task. We establish necessary and sufficient conditions for these structures to satisfy for information-feedback policies that can be defined over the states of an internal system to exist. We also show that under mild assumptions, minimal internal systems that can represent a particular plan/policy described over the action-observation histories exist and are unique. Finally, the results are applied to determine sufficient structures for distance-optimal navigation in a polygonal environment.

Universal Plans: One Action Sequence to Solve Them All!

This paper introduces the notion of a universal plan, which when executed, is guaranteed to solve all planning problems in a category, regardless of the obstacles, initial state, and goal set. Such plans are specified as a deterministic sequence of actions that are blindly applied without any sensor feedback. Thus, they can be considered as pure exploration in a reinforcement learning context, and we show that with basic memory requirements, they even yield asymptotically optimal plans. Building upon results in number theory and theory of automata, we provide universal plans both for discrete and continuous (motion) planning and prove their (semi)completeness. The concepts are applied and illustrated through simulation studies, and several directions for future research are sketched.

An Internal Model Principle For Robots

When designing a robot's internal system, one often makes assumptions about the structure of the intended environment of the robot. One may even assign meaning to various internal components of the robot in terms of expected environmental correlates. In this paper we want to make the distinction between robot's internal and external worlds clear-cut. Can the robot learn about its environment, relying only on internally available information, including the sensor data? Are there mathematical conditions on the internal robot system which can be internally verified and make the robot's internal system mirror the structure of the environment? We prove that sufficiency is such a mathematical principle, and mathematically describe the emergence of the robot's internal structure isomorphic or bisimulation equivalent to that of the environment. A connection to the free-energy principle is established, when sufficiency is interpreted as a limit case of surprise minimization. As such, we show that surprise minimization leads to having an internal model isomorphic to the environment. This also parallels the Good Regulator Principle which states that controlling a system sufficiently well means having a model of it. Unlike the mentioned theories, ours is discrete, and non-probabilistic.

Equivalent Environments and Covering Spaces for Robots

This paper formally defines a robot system, including its sensing and actuation components, as a general, topological dynamical system. The focus is on determining general conditions under which various environments in which the robot can be placed are indistinguishable. A key result is that, under very general conditions, covering maps witness such indistinguishability. This formalizes the intuition behind the well studied loop closure problem in robotics. An important special case is where the sensor mapping reports an invariant of the local topological (metric) structure of an environment because such structure is preserved by (metric) covering maps. Whereas coverings provide a sufficient condition for the equivalence of environments, we also give a necessary condition using bisimulation. The overall framework is applied to unify previously identified phenomena in robotics and related fields, in which moving agents with sensors must make inferences about their environments based on limited data. Many open problems are identified.

A Mathematical Characterization of Minimally Sufficient Robot Brains

This paper addresses the lower limits of encoding and processing the information acquired through interactions between an internal system (robot algorithms or software) and an external system (robot body and its environment) in terms of action and observation histories. Both are modeled as transition systems. We want to know the weakest internal system that is sufficient for achieving passive (filtering) and active (planning) tasks. We introduce the notion of an information transition system for the internal system which is a transition system over a space of information states that reflect a robot's or other observer's perspective based on limited sensing, memory, computation, and actuation. An information transition system is viewed as a filter and a policy or plan is viewed as a function that labels the states of this information transition system. Regardless of whether internal systems are obtained by learning algorithms, planning algorithms, or human insight, we want to know the limits of feasibility for given robot hardware and tasks. We establish, in a general setting, that minimal information transition systems exist up to reasonable equivalence assumptions, and are unique under some general conditions. We then apply the theory to generate new insights into several problems, including optimal sensor fusion/filtering, solving basic planning tasks, and finding minimal representations for modeling a system given input-output relations.

The Limits of Learning and Planning: Minimal Sufficient Information Transition Systems

In this paper, we view a policy or plan as a transition system over a space of information states that reflect a robot's or other observer's perspective based on limited sensing, memory, computation, and actuation. Regardless of whether policies are obtained by learning algorithms, planning algorithms, or human insight, we want to know the limits of feasibility for given robot hardware and tasks. Toward the quest to find the best policies, we establish in a general setting that minimal information transition systems (ITSs) exist up to reasonable equivalence assumptions, and are unique under some general conditions. We then apply the theory to generate new insights into several problems, including optimal sensor fusion/filtering, solving basic planning tasks, and finding minimal representations for feasible policies.

Bang-Bang Boosting of RRTs

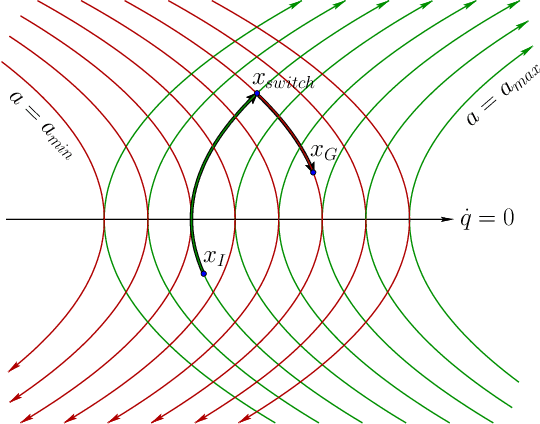
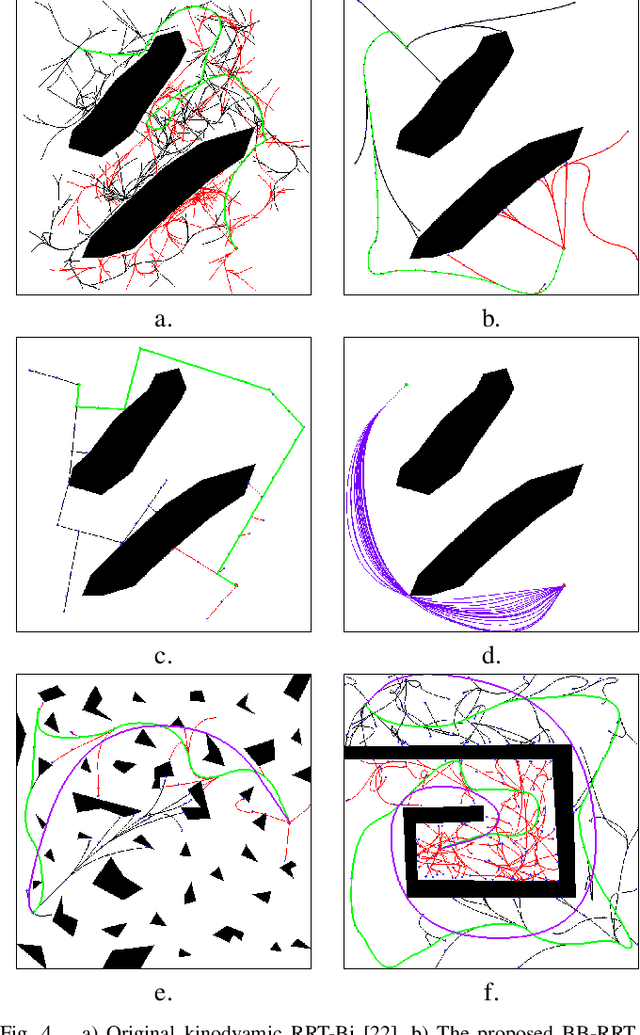
This paper explores the use of time-optimal controls to improve the performance of sampling-based kinodynamic planners. A computationally efficient steering method is introduced that produces time-optimal trajectories between any states for a vector of double integrators. This method is applied in three ways: 1) to generate RRT edges that quickly solve the two-point boundary-value problems, 2) to produce an RRT (quasi)metric for more accurate Voronoi bias, and 3) to time-optimize a given collision-free trajectory. Experiments are performed for state spaces with up to 2000 dimensions, resulting in improved computed trajectories and orders of magnitude computation time improvements over using ordinary metrics and constant controls.

Localization with Few Distance Measurements

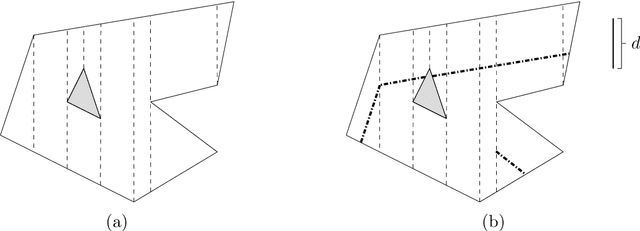
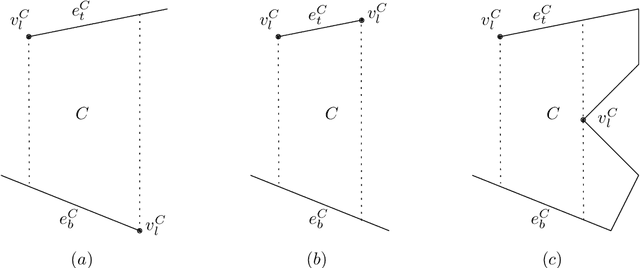
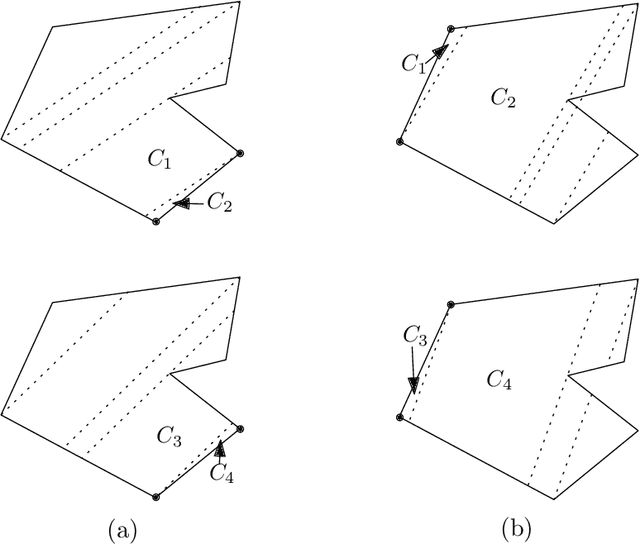
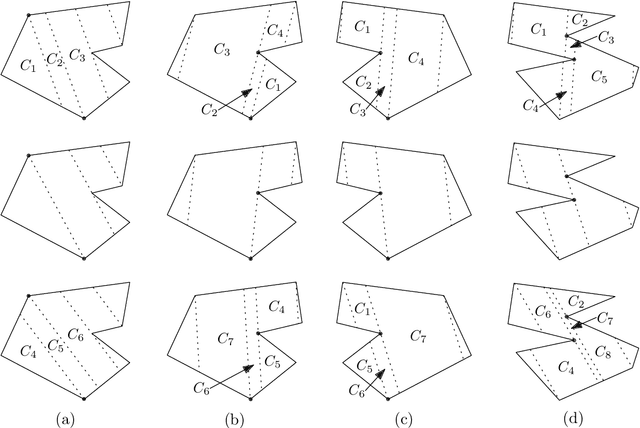
Given a polygon $W$, a depth sensor placed at point $p=(x,y)$ inside $W$ and oriented in direction $\theta$ measures the distance $d=h(x,y,\theta)$ between $p$ and the closest point on the boundary of $W$ along a ray emanating from $p$ in direction $\theta$. We study the following problem: Give a polygon $W$, possibly with holes, with $n$ vertices, preprocess it such that given a query real value $d\geq 0$, one can efficiently compute the preimage $h^{-1}(d)$, namely determine all the possible poses (positions and orientations) of a depth sensor placed in $W$ that would yield the reading $d$. We employ a decomposition of $W\times S^1$, which is an extension of the celebrated trapezoidal decomposition, and which we call rotational trapezoidal decomposition and present an efficient data structure, which computes the preimage in an output-sensitive fashion relative to this decomposition: if $k$ cells of the decomposition contribute to the final result, we will report them in $O(k+1)$ time, after $O(n^2\log n)$ preprocessing time and using $O(n^2)$ storage space. We also analyze the shape of the projection of the preimage onto the polygon $W$; this projection describes the portion of $W$ where the sensor could have been placed. Furthermore, we obtain analogous results for the more useful case (narrowing down the set of possible poses), where the sensor performs two depth measurement from the same point $p$, one in direction $\theta$ and the other in direction $\theta+\pi$. While localizations problems in robotics are often carried out by exploring the full visibility polygon of a sensor placed at a fixed point of the environment, the approach that we propose here opens the door to sufficing with only few depth measurements, which is advantageous as it allows for usage of inexpensive sensors and could also lead to savings in storage and communication costs.