Bang-Bang Boosting of RRTs
Paper and Code
Oct 04, 2022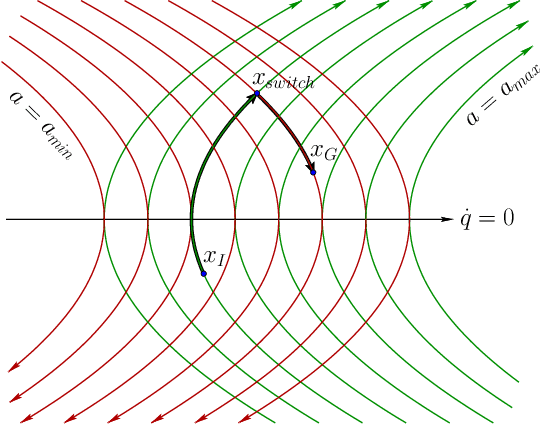


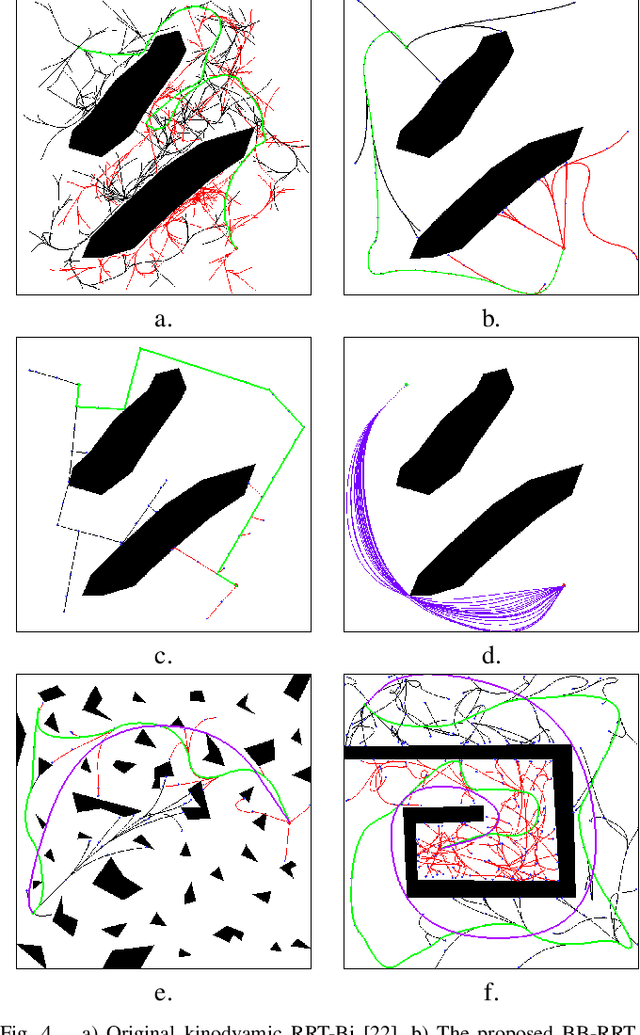
This paper explores the use of time-optimal controls to improve the performance of sampling-based kinodynamic planners. A computationally efficient steering method is introduced that produces time-optimal trajectories between any states for a vector of double integrators. This method is applied in three ways: 1) to generate RRT edges that quickly solve the two-point boundary-value problems, 2) to produce an RRT (quasi)metric for more accurate Voronoi bias, and 3) to time-optimize a given collision-free trajectory. Experiments are performed for state spaces with up to 2000 dimensions, resulting in improved computed trajectories and orders of magnitude computation time improvements over using ordinary metrics and constant controls.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge