Universal Plans: One Action Sequence to Solve Them All!

This paper introduces the notion of a universal plan, which when executed, is guaranteed to solve all planning problems in a category, regardless of the obstacles, initial state, and goal set. Such plans are specified as a deterministic sequence of actions that are blindly applied without any sensor feedback. Thus, they can be considered as pure exploration in a reinforcement learning context, and we show that with basic memory requirements, they even yield asymptotically optimal plans. Building upon results in number theory and theory of automata, we provide universal plans both for discrete and continuous (motion) planning and prove their (semi)completeness. The concepts are applied and illustrated through simulation studies, and several directions for future research are sketched.

Bang-Bang Boosting of RRTs

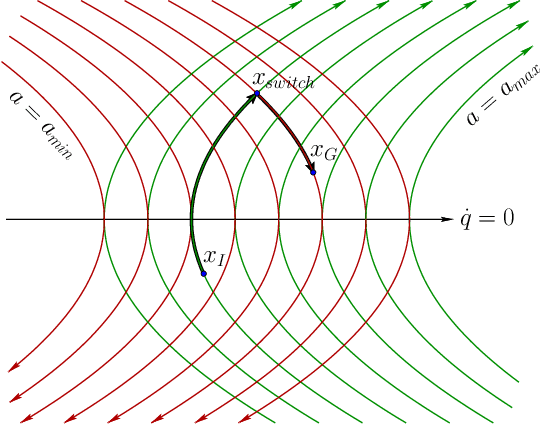
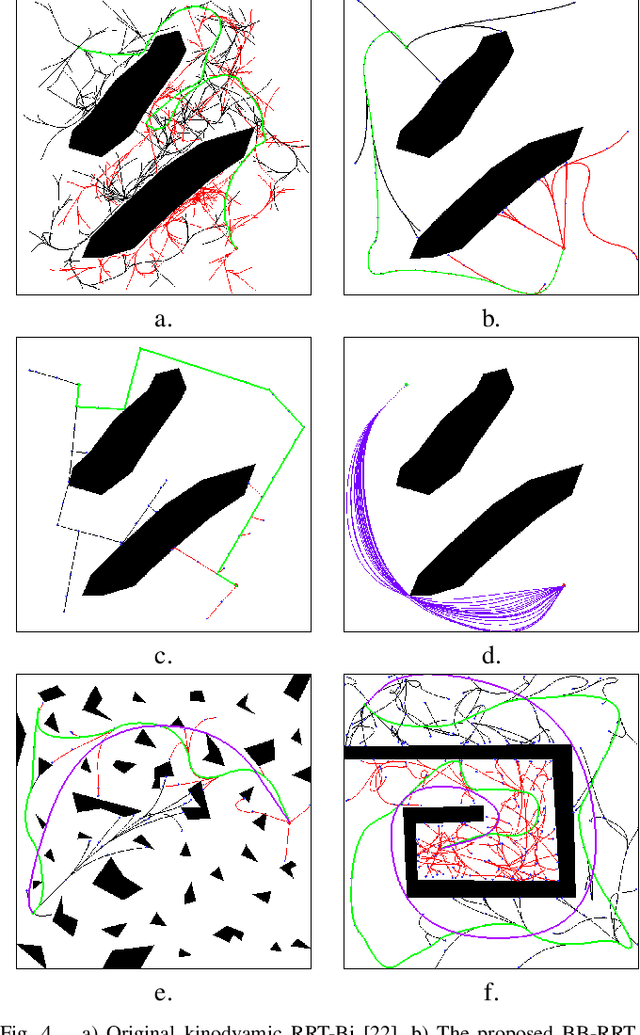
This paper explores the use of time-optimal controls to improve the performance of sampling-based kinodynamic planners. A computationally efficient steering method is introduced that produces time-optimal trajectories between any states for a vector of double integrators. This method is applied in three ways: 1) to generate RRT edges that quickly solve the two-point boundary-value problems, 2) to produce an RRT (quasi)metric for more accurate Voronoi bias, and 3) to time-optimize a given collision-free trajectory. Experiments are performed for state spaces with up to 2000 dimensions, resulting in improved computed trajectories and orders of magnitude computation time improvements over using ordinary metrics and constant controls.