Coordination of Multiple Robots along Given Paths with Bounded Junction Complexity

We study a fundamental NP-hard motion coordination problem for multi-robot/multi-agent systems: We are given a graph $G$ and set of agents, where each agent has a given directed path in $G$. Each agent is initially located on the first vertex of its path. At each time step an agent can move to the next vertex on its path, provided that the vertex is not occupied by another agent. The goal is to find a sequence of such moves along the given paths so that each reaches its target, or to report that no such sequence exists. The problem models guidepath-based transport systems, which is a pertinent abstraction for traffic in a variety of contemporary applications, ranging from train networks or Automated Guided Vehicles (AGVs) in factories, through computer game animations, to qubit transport in quantum computing. It also arises as a sub-problem in the more general multi-robot motion-planning problem. We provide a fine-grained tractability analysis of the problem by considering new assumptions and identifying minimal values of key parameters for which the problem remains NP-hard. Our analysis identifies a critical parameter called vertex multiplicity (VM), defined as the maximum number of paths passing through the same vertex. We show that a prevalent variant of the problem, which is equivalent to Sequential Resource Allocation (concerning deadlock prevention for concurrent processes), is NP-hard even when VM is 3. On the positive side, for VM $\le$ 2 we give an efficient algorithm that iteratively resolves cycles of blocking relations among agents. We also present a variant that is NP-hard when the VM is 2 even when $G$ is a 2D grid and each path lies in a single grid row or column. By studying highly distilled yet NP-hard variants, we deepen the understanding of what makes the problem intractable and thereby guide the search for efficient solutions under practical assumptions.

Localization with Few Distance Measurements

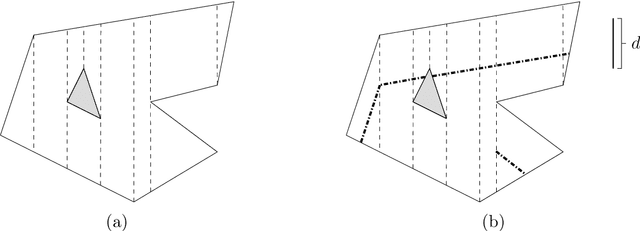
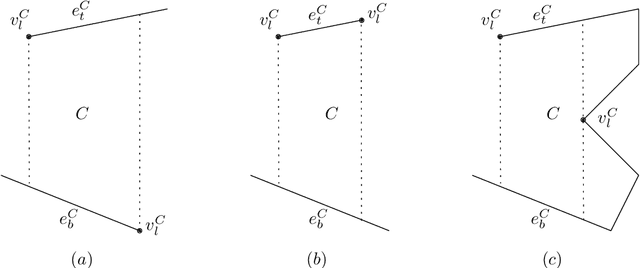
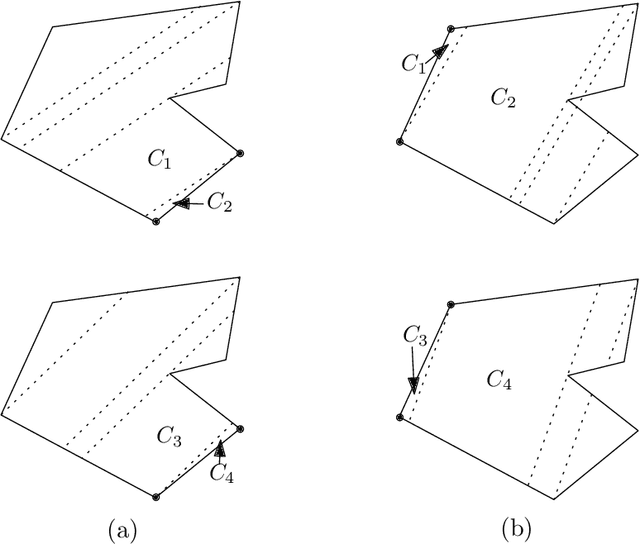
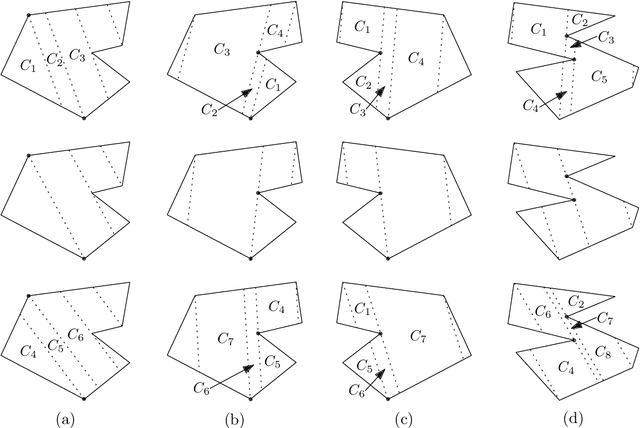
Given a polygon $W$, a depth sensor placed at point $p=(x,y)$ inside $W$ and oriented in direction $\theta$ measures the distance $d=h(x,y,\theta)$ between $p$ and the closest point on the boundary of $W$ along a ray emanating from $p$ in direction $\theta$. We study the following problem: Give a polygon $W$, possibly with holes, with $n$ vertices, preprocess it such that given a query real value $d\geq 0$, one can efficiently compute the preimage $h^{-1}(d)$, namely determine all the possible poses (positions and orientations) of a depth sensor placed in $W$ that would yield the reading $d$. We employ a decomposition of $W\times S^1$, which is an extension of the celebrated trapezoidal decomposition, and which we call rotational trapezoidal decomposition and present an efficient data structure, which computes the preimage in an output-sensitive fashion relative to this decomposition: if $k$ cells of the decomposition contribute to the final result, we will report them in $O(k+1)$ time, after $O(n^2\log n)$ preprocessing time and using $O(n^2)$ storage space. We also analyze the shape of the projection of the preimage onto the polygon $W$; this projection describes the portion of $W$ where the sensor could have been placed. Furthermore, we obtain analogous results for the more useful case (narrowing down the set of possible poses), where the sensor performs two depth measurement from the same point $p$, one in direction $\theta$ and the other in direction $\theta+\pi$. While localizations problems in robotics are often carried out by exploring the full visibility polygon of a sensor placed at a fixed point of the environment, the approach that we propose here opens the door to sufficing with only few depth measurements, which is advantageous as it allows for usage of inexpensive sensors and could also lead to savings in storage and communication costs.