Near-Optimal Min-Sum Motion Planning for Two Square Robots in a Polygonal Environment

Let $\mathcal{W} \subset \mathbb{R}^2$ be a planar polygonal environment (i.e., a polygon potentially with holes) with a total of $n$ vertices, and let $A,B$ be two robots, each modeled as an axis-aligned unit square, that can translate inside $\mathcal{W}$. Given source and target placements $s_A,t_A,s_B,t_B \in \mathcal{W}$ of $A$ and $B$, respectively, the goal is to compute a \emph{collision-free motion plan} $\mathbf{\pi}^*$, i.e., a motion plan that continuously moves $A$ from $s_A$ to $t_A$ and $B$ from $s_B$ to $t_B$ so that $A$ and $B$ remain inside $\mathcal{W}$ and do not collide with each other during the motion. Furthermore, if such a plan exists, then we wish to return a plan that minimizes the sum of the lengths of the paths traversed by the robots, $\left|\mathbf{\pi}^*\right|$. Given $\mathcal{W}, s_A,t_A,s_B,t_B$ and a parameter $\varepsilon > 0$, we present an $n^2\varepsilon^{-O(1)} \log n$-time $(1+\varepsilon)$-approximation algorithm for this problem. We are not aware of any polynomial time algorithm for this problem, nor do we know whether the problem is NP-Hard. Our result is the first polynomial-time $(1+\varepsilon)$-approximation algorithm for an optimal motion planning problem involving two robots moving in a polygonal environment.

How to Find a Point in the Convex Hull Privately

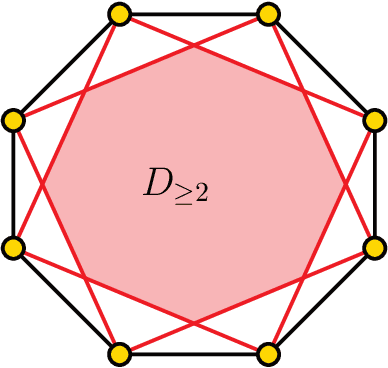
We study the question of how to compute a point in the convex hull of an input set $S$ of $n$ points in ${\mathbb R}^d$ in a differentially private manner. This question, which is trivial non-privately, turns out to be quite deep when imposing differential privacy. In particular, it is known that the input points must reside on a fixed finite subset $G\subseteq{\mathbb R}^d$, and furthermore, the size of $S$ must grow with the size of $G$. Previous works focused on understanding how $n$ needs to grow with $|G|$, and showed that $n=O\left(d^{2.5}\cdot8^{\log^*|G|}\right)$ suffices (so $n$ does not have to grow significantly with $|G|$). However, the available constructions exhibit running time at least $|G|^{d^2}$, where typically $|G|=X^d$ for some (large) discretization parameter $X$, so the running time is in fact $\Omega(X^{d^3})$. In this paper we give a differentially private algorithm that runs in $O(n^d)$ time, assuming that $n=\Omega(d^4\log X)$. To get this result we study and exploit some structural properties of the Tukey levels (the regions $D_{\ge k}$ consisting of points whose Tukey depth is at least $k$, for $k=0,1,...$). In particular, we derive lower bounds on their volumes for point sets $S$ in general position, and develop a rather subtle mechanism for handling point sets $S$ in degenerate position (where the deep Tukey regions have zero volume). A naive approach to the construction of the Tukey regions requires $n^{O(d^2)}$ time. To reduce the cost to $O(n^d)$, we use an approximation scheme for estimating the volumes of the Tukey regions (within their affine spans in case of degeneracy), and for sampling a point from such a region, a scheme that is based on the volume estimation framework of Lov\'asz and Vempala (FOCS 2003) and of Cousins and Vempala (STOC 2015). Making this framework differentially private raises a set of technical challenges that we address.