Near-Optimal Min-Sum Motion Planning for Two Square Robots in a Polygonal Environment

Let $\mathcal{W} \subset \mathbb{R}^2$ be a planar polygonal environment (i.e., a polygon potentially with holes) with a total of $n$ vertices, and let $A,B$ be two robots, each modeled as an axis-aligned unit square, that can translate inside $\mathcal{W}$. Given source and target placements $s_A,t_A,s_B,t_B \in \mathcal{W}$ of $A$ and $B$, respectively, the goal is to compute a \emph{collision-free motion plan} $\mathbf{\pi}^*$, i.e., a motion plan that continuously moves $A$ from $s_A$ to $t_A$ and $B$ from $s_B$ to $t_B$ so that $A$ and $B$ remain inside $\mathcal{W}$ and do not collide with each other during the motion. Furthermore, if such a plan exists, then we wish to return a plan that minimizes the sum of the lengths of the paths traversed by the robots, $\left|\mathbf{\pi}^*\right|$. Given $\mathcal{W}, s_A,t_A,s_B,t_B$ and a parameter $\varepsilon > 0$, we present an $n^2\varepsilon^{-O(1)} \log n$-time $(1+\varepsilon)$-approximation algorithm for this problem. We are not aware of any polynomial time algorithm for this problem, nor do we know whether the problem is NP-Hard. Our result is the first polynomial-time $(1+\varepsilon)$-approximation algorithm for an optimal motion planning problem involving two robots moving in a polygonal environment.

Multi-Robot Motion Planning for Unit Discs with Revolving Areas

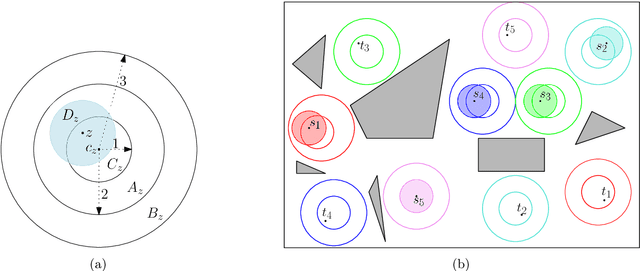
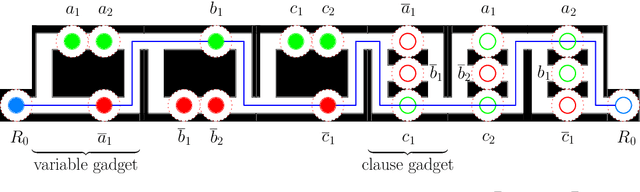
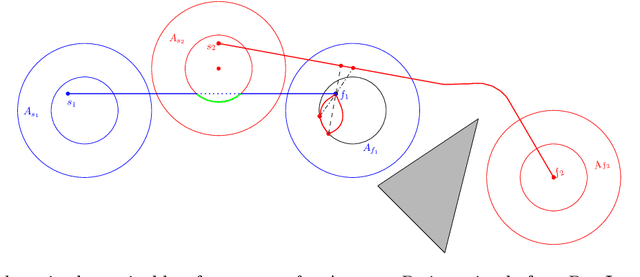
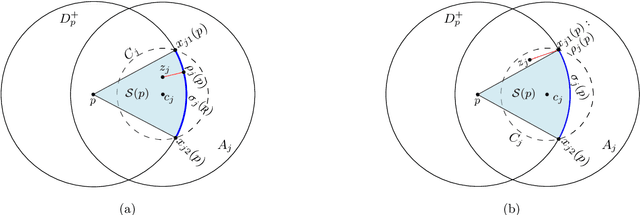
We study the problem of motion planning for a collection of $n$ labeled unit disc robots in a polygonal environment. We assume that the robots have \emph{revolving areas} around their start and final positions: that each start and each final is contained in a radius $2$ disc lying in the free space, not necessarily concentric with the start or final position, which is free from other start or final positions. This assumption allows a \emph{weakly-monotone} motion plan, in which robots move according to an ordering as follows: during the turn of a robot $R$ in the ordering, it moves fully from its start to final position, while other robots do not leave their revolving areas. As $R$ passes through a revolving area, a robot $R'$ that is inside this area may move within the revolving area to avoid a collision. Notwithstanding the existence of a motion plan, we show that minimizing the total traveled distance in this setting, specifically even when the motion plan is restricted to be weakly-monotone, is APX-hard, ruling out any polynomial-time $(1+\epsilon)$-approximation algorithm. On the positive side, we present the first constant-factor approximation algorithm for computing a feasible weakly-monotone motion plan. The total distance traveled by the robots is within an $O(1)$ factor of that of the optimal motion plan, which need not be weakly monotone. Our algorithm extends to an online setting in which the polygonal environment is fixed but the initial and final positions of robots are specified in an online manner. Finally, we observe that the overhead in the overall cost that we add while editing the paths to avoid robot-robot collision can vary significantly depending on the ordering we chose. Finding the best ordering in this respect is known to be NP-hard, and we provide a polynomial time $O(\log n \log \log n)$-approximation algorithm for this problem.

On Two-Handed Planar Assembly Partitioning

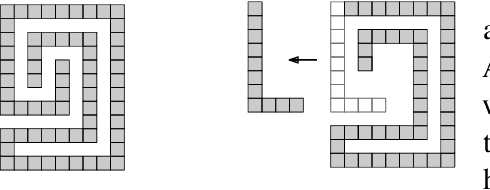
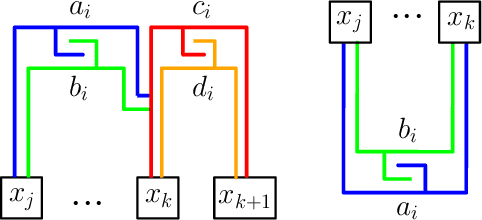
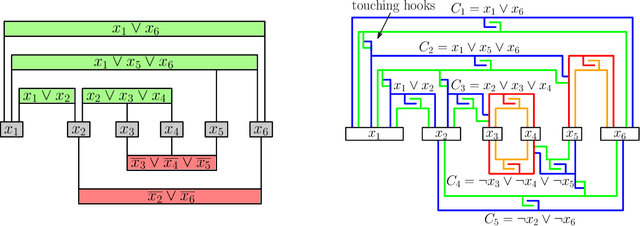
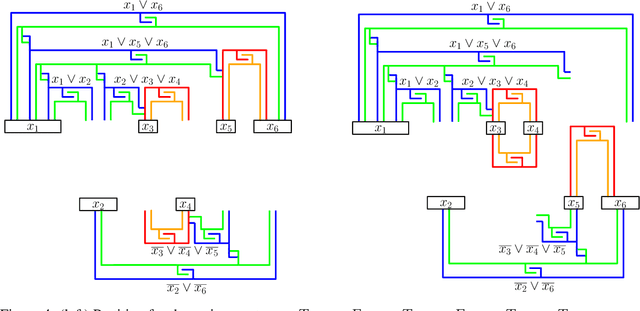
Assembly planning, which is a fundamental problem in robotics and automation, aims to design a sequence of motions that will bring the separate constituent parts of a product into their final placement in the product. It is convenient to study assembly planning in reverse order, where the following key problem, assembly partitioning, arises: Given a set of parts in their final placement in a product, partition them into two sets, each regarded as a rigid body, which we call a subassembly, such that these two subassemblies can be moved sufficiently far away from each other, without colliding with one another. The basic assembly planning problem is further complicated by practical consideration such as how to hold the parts in a subassembly together. Therefore, a desired property of a valid assembly partition is that each of the two subassemblies will be connected. We show that even an utterly simple case of the connected-assembly-partitioning problem is hard: Given a connected set $A$ of unit squares in the plane, each forming a distinct cell of the uniform integer grid, find a subset $S\subset A$ such that $S$ can be rigidly translated to infinity along a prescribed direction without colliding with $A\setminus S$, and both subassemblies $S$ and $A\setminus S$ are each connected. We show that this problem is NP-Complete, and by that settle an open problem posed by Wilson et al. (1995) a quarter of a century ago. We complement the hardness result with two positive results for the aforementioned problem variant of grid squares. First, we show that it is fixed parameter tractable and give an $O(2^k n^2)$-time algorithm, where $n=|A|$ and $k=|S|$. Second, we describe a special case of this variant where a connected partition can always be found in linear time. Each of the positive results sheds further light on the special geometric structure of the problem at hand.

An Efficient Algorithm for Computing High-Quality Paths amid Polygonal Obstacles

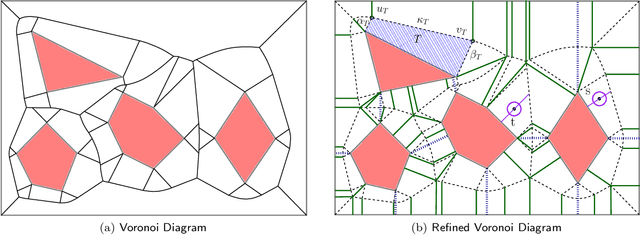
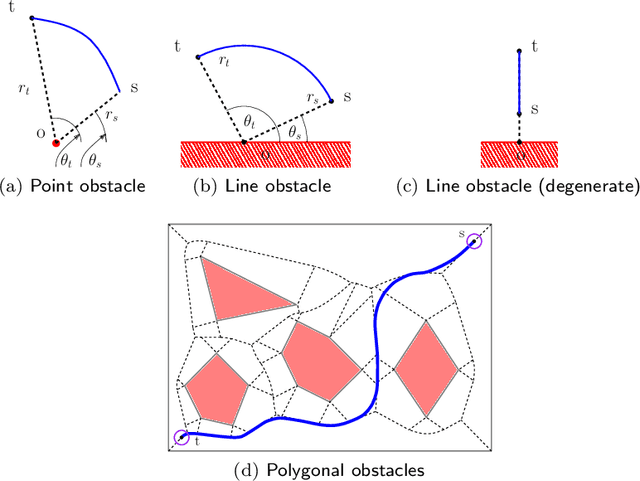
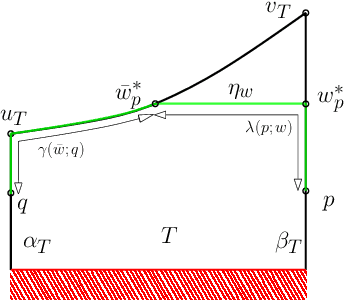
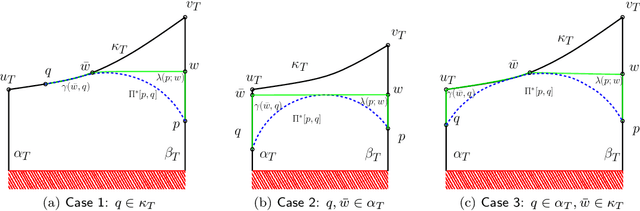
We study a path-planning problem amid a set $\mathcal{O}$ of obstacles in $\mathbb{R}^2$, in which we wish to compute a short path between two points while also maintaining a high clearance from $\mathcal{O}$; the clearance of a point is its distance from a nearest obstacle in $\mathcal{O}$. Specifically, the problem asks for a path minimizing the reciprocal of the clearance integrated over the length of the path. We present the first polynomial-time approximation scheme for this problem. Let $n$ be the total number of obstacle vertices and let $\varepsilon \in (0,1]$. Our algorithm computes in time $O(\frac{n^2}{\varepsilon ^2} \log \frac{n}{\varepsilon})$ a path of total cost at most $(1+\varepsilon)$ times the cost of the optimal path.

Sparsification of Motion-Planning Roadmaps by Edge Contraction

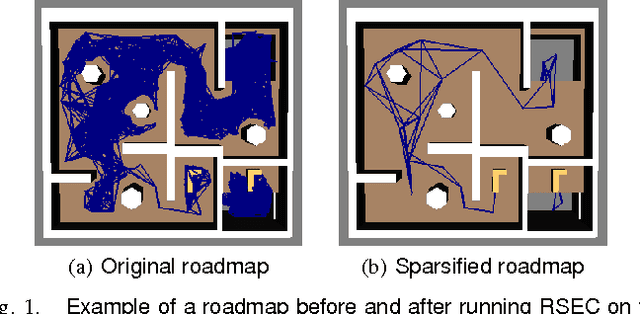
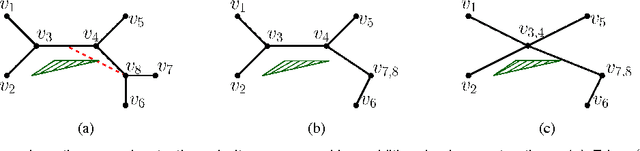
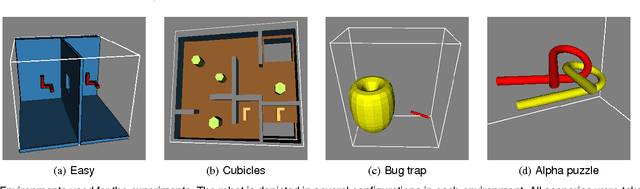
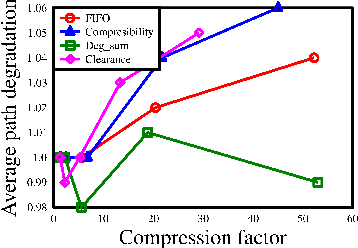
We present Roadmap Sparsification by Edge Contraction (RSEC), a simple and effective algorithm for reducing the size of a motion-planning roadmap. The algorithm exhibits minimal effect on the quality of paths that can be extracted from the new roadmap. The primitive operation used by RSEC is edge contraction - the contraction of a roadmap edge to a single vertex and the connection of the new vertex to the neighboring vertices of the contracted edge. For certain scenarios, we compress more than 98% of the edges and vertices at the cost of degradation of average shortest path length by at most 2%.