Boris Aronov
On Two-Handed Planar Assembly Partitioning
Sep 25, 2020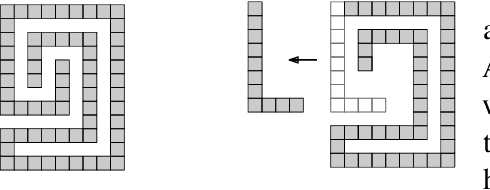
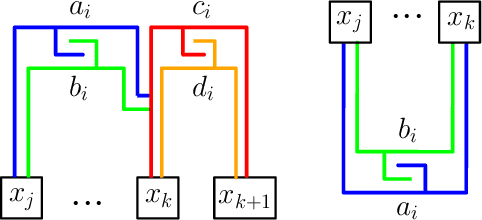
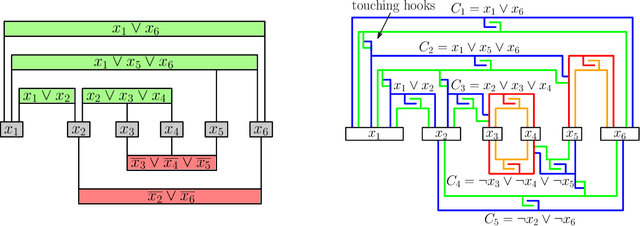
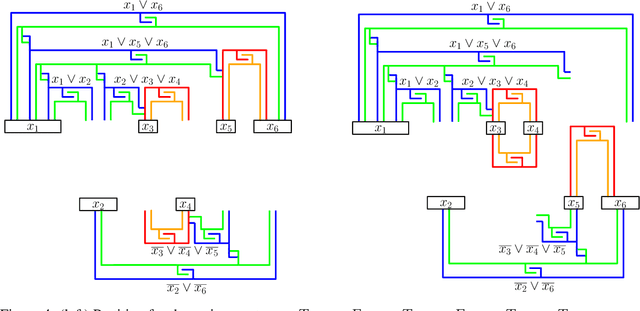
Abstract:Assembly planning, which is a fundamental problem in robotics and automation, aims to design a sequence of motions that will bring the separate constituent parts of a product into their final placement in the product. It is convenient to study assembly planning in reverse order, where the following key problem, assembly partitioning, arises: Given a set of parts in their final placement in a product, partition them into two sets, each regarded as a rigid body, which we call a subassembly, such that these two subassemblies can be moved sufficiently far away from each other, without colliding with one another. The basic assembly planning problem is further complicated by practical consideration such as how to hold the parts in a subassembly together. Therefore, a desired property of a valid assembly partition is that each of the two subassemblies will be connected. We show that even an utterly simple case of the connected-assembly-partitioning problem is hard: Given a connected set $A$ of unit squares in the plane, each forming a distinct cell of the uniform integer grid, find a subset $S\subset A$ such that $S$ can be rigidly translated to infinity along a prescribed direction without colliding with $A\setminus S$, and both subassemblies $S$ and $A\setminus S$ are each connected. We show that this problem is NP-Complete, and by that settle an open problem posed by Wilson et al. (1995) a quarter of a century ago. We complement the hardness result with two positive results for the aforementioned problem variant of grid squares. First, we show that it is fixed parameter tractable and give an $O(2^k n^2)$-time algorithm, where $n=|A|$ and $k=|S|$. Second, we describe a special case of this variant where a connected partition can always be found in linear time. Each of the positive results sheds further light on the special geometric structure of the problem at hand.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge