An Efficient Algorithm for Computing High-Quality Paths amid Polygonal Obstacles
Paper and Code
Jun 09, 2017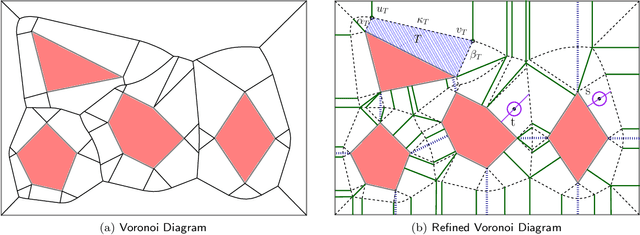
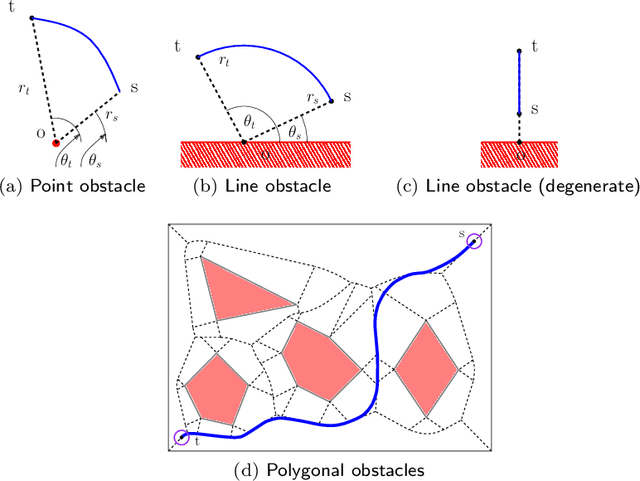
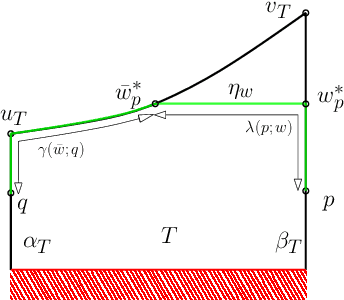
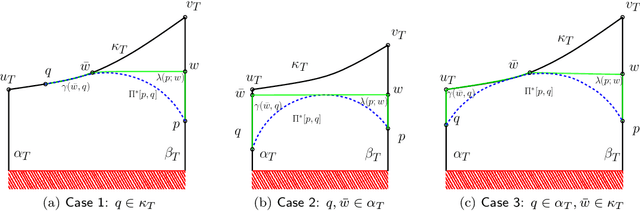
We study a path-planning problem amid a set $\mathcal{O}$ of obstacles in $\mathbb{R}^2$, in which we wish to compute a short path between two points while also maintaining a high clearance from $\mathcal{O}$; the clearance of a point is its distance from a nearest obstacle in $\mathcal{O}$. Specifically, the problem asks for a path minimizing the reciprocal of the clearance integrated over the length of the path. We present the first polynomial-time approximation scheme for this problem. Let $n$ be the total number of obstacle vertices and let $\varepsilon \in (0,1]$. Our algorithm computes in time $O(\frac{n^2}{\varepsilon ^2} \log \frac{n}{\varepsilon})$ a path of total cost at most $(1+\varepsilon)$ times the cost of the optimal path.
* A preliminary version of this work appear in the Proceedings of the
27th Annual ACM-SIAM Symposium on Discrete Algorithms
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge