Efficient Calibration for Decision Making

A decision-theoretic characterization of perfect calibration is that an agent seeking to minimize a proper loss in expectation cannot improve their outcome by post-processing a perfectly calibrated predictor. Hu and Wu (FOCS'24) use this to define an approximate calibration measure called calibration decision loss ($\mathsf{CDL}$), which measures the maximal improvement achievable by any post-processing over any proper loss. Unfortunately, $\mathsf{CDL}$ turns out to be intractable to even weakly approximate in the offline setting, given black-box access to the predictions and labels. We suggest circumventing this by restricting attention to structured families of post-processing functions $K$. We define the calibration decision loss relative to $K$, denoted $\mathsf{CDL}_K$ where we consider all proper losses but restrict post-processings to a structured family $K$. We develop a comprehensive theory of when $\mathsf{CDL}_K$ is information-theoretically and computationally tractable, and use it to prove both upper and lower bounds for natural classes $K$. In addition to introducing new definitions and algorithmic techniques to the theory of calibration for decision making, our results give rigorous guarantees for some widely used recalibration procedures in machine learning.

How Global Calibration Strengthens Multiaccuracy

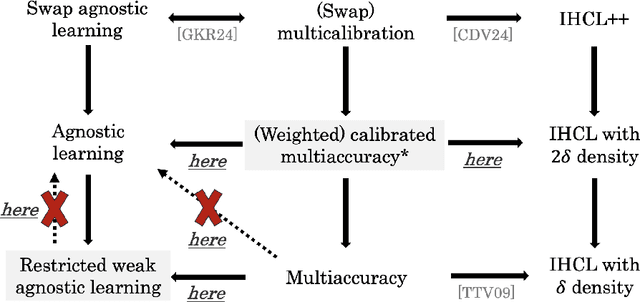
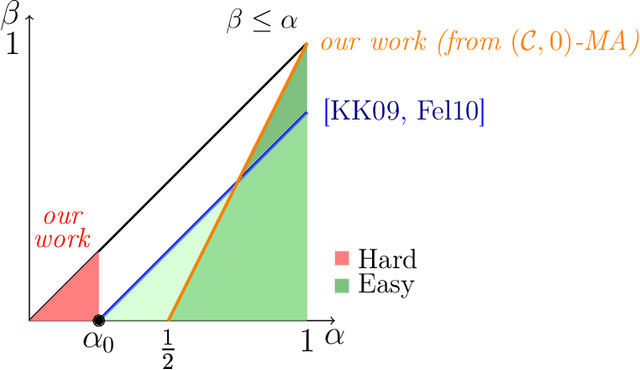
Multiaccuracy and multicalibration are multigroup fairness notions for prediction that have found numerous applications in learning and computational complexity. They can be achieved from a single learning primitive: weak agnostic learning. Here we investigate the power of multiaccuracy as a learning primitive, both with and without the additional assumption of calibration. We find that multiaccuracy in itself is rather weak, but that the addition of global calibration (this notion is called calibrated multiaccuracy) boosts its power substantially, enough to recover implications that were previously known only assuming the stronger notion of multicalibration. We give evidence that multiaccuracy might not be as powerful as standard weak agnostic learning, by showing that there is no way to post-process a multiaccurate predictor to get a weak learner, even assuming the best hypothesis has correlation $1/2$. Rather, we show that it yields a restricted form of weak agnostic learning, which requires some concept in the class to have correlation greater than $1/2$ with the labels. However, by also requiring the predictor to be calibrated, we recover not just weak, but strong agnostic learning. A similar picture emerges when we consider the derivation of hardcore measures from predictors satisfying multigroup fairness notions. On the one hand, while multiaccuracy only yields hardcore measures of density half the optimal, we show that (a weighted version of) calibrated multiaccuracy achieves optimal density. Our results yield new insights into the complementary roles played by multiaccuracy and calibration in each setting. They shed light on why multiaccuracy and global calibration, although not particularly powerful by themselves, together yield considerably stronger notions.

When does a predictor know its own loss?

Given a predictor and a loss function, how well can we predict the loss that the predictor will incur on an input? This is the problem of loss prediction, a key computational task associated with uncertainty estimation for a predictor. In a classification setting, a predictor will typically predict a distribution over labels and hence have its own estimate of the loss that it will incur, given by the entropy of the predicted distribution. Should we trust this estimate? In other words, when does the predictor know what it knows and what it does not know? In this work we study the theoretical foundations of loss prediction. Our main contribution is to establish tight connections between nontrivial loss prediction and certain forms of multicalibration, a multigroup fairness notion that asks for calibrated predictions across computationally identifiable subgroups. Formally, we show that a loss predictor that is able to improve on the self-estimate of a predictor yields a witness to a failure of multicalibration, and vice versa. This has the implication that nontrivial loss prediction is in effect no easier or harder than auditing for multicalibration. We support our theoretical results with experiments that show a robust positive correlation between the multicalibration error of a predictor and the efficacy of training a loss predictor.

Provable Uncertainty Decomposition via Higher-Order Calibration

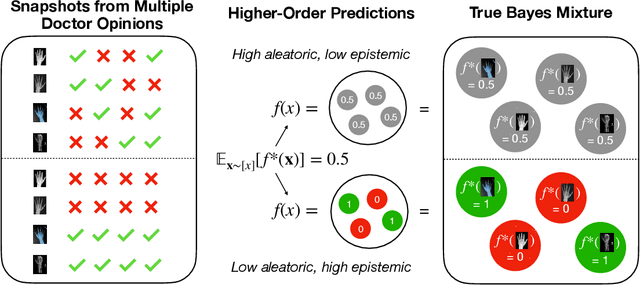
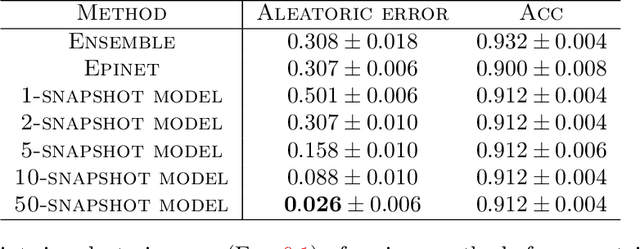
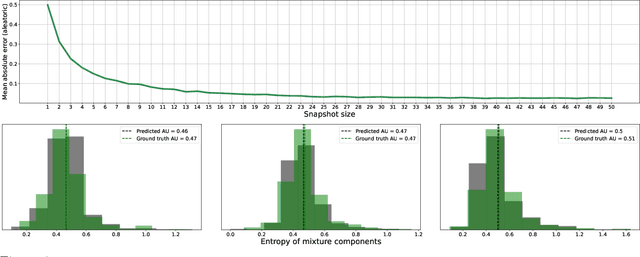
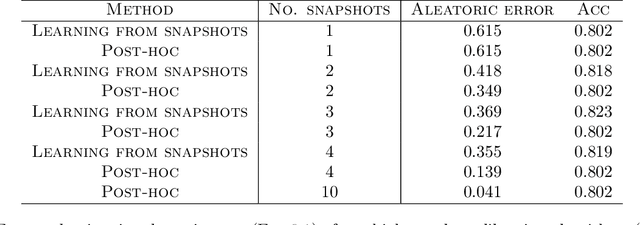
We give a principled method for decomposing the predictive uncertainty of a model into aleatoric and epistemic components with explicit semantics relating them to the real-world data distribution. While many works in the literature have proposed such decompositions, they lack the type of formal guarantees we provide. Our method is based on the new notion of higher-order calibration, which generalizes ordinary calibration to the setting of higher-order predictors that predict mixtures over label distributions at every point. We show how to measure as well as achieve higher-order calibration using access to $k$-snapshots, namely examples where each point has $k$ independent conditional labels. Under higher-order calibration, the estimated aleatoric uncertainty at a point is guaranteed to match the real-world aleatoric uncertainty averaged over all points where the prediction is made. To our knowledge, this is the first formal guarantee of this type that places no assumptions whatsoever on the real-world data distribution. Importantly, higher-order calibration is also applicable to existing higher-order predictors such as Bayesian and ensemble models and provides a natural evaluation metric for such models. We demonstrate through experiments that our method produces meaningful uncertainty decompositions for image classification.

Learning to Route with Confidence Tokens

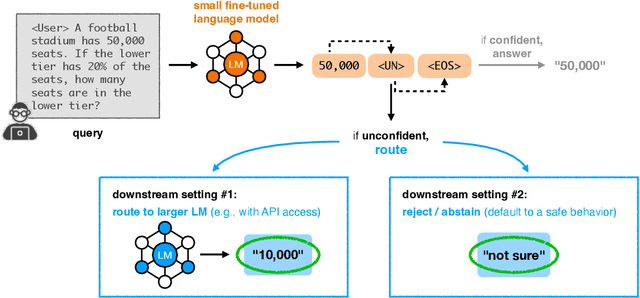
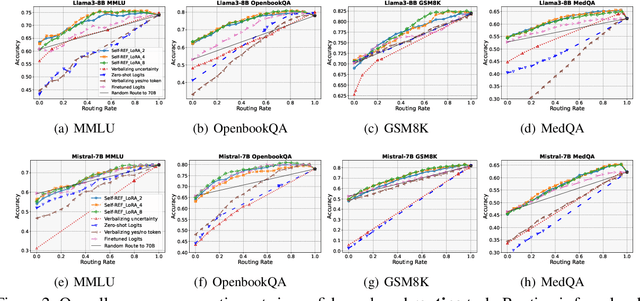
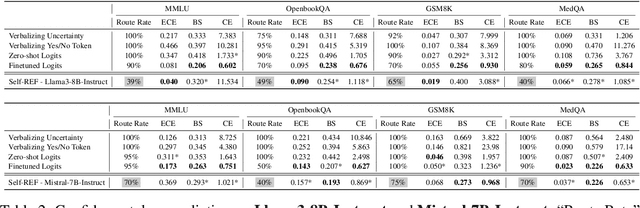
Large language models (LLMs) have demonstrated impressive performance on several tasks and are increasingly deployed in real-world applications. However, especially in high-stakes settings, it becomes vital to know when the output of an LLM may be unreliable. Depending on whether an answer is trustworthy, a system can then choose to route the question to another expert, or otherwise fall back on a safe default behavior. In this work, we study the extent to which LLMs can reliably indicate confidence in their answers, and how this notion of confidence can translate into downstream accuracy gains. We propose Self-REF, a lightweight training strategy to teach LLMs to express confidence in whether their answers are correct in a reliable manner. Self-REF introduces confidence tokens into the LLM, from which a confidence score can be extracted. Compared to conventional approaches such as verbalizing confidence and examining token probabilities, we demonstrate empirically that confidence tokens show significant improvements in downstream routing and rejection learning tasks.

On Computationally Efficient Multi-Class Calibration

Consider a multi-class labelling problem, where the labels can take values in $[k]$, and a predictor predicts a distribution over the labels. In this work, we study the following foundational question: Are there notions of multi-class calibration that give strong guarantees of meaningful predictions and can be achieved in time and sample complexities polynomial in $k$? Prior notions of calibration exhibit a tradeoff between computational efficiency and expressivity: they either suffer from having sample complexity exponential in $k$, or needing to solve computationally intractable problems, or give rather weak guarantees. Our main contribution is a notion of calibration that achieves all these desiderata: we formulate a robust notion of projected smooth calibration for multi-class predictions, and give new recalibration algorithms for efficiently calibrating predictors under this definition with complexity polynomial in $k$. Projected smooth calibration gives strong guarantees for all downstream decision makers who want to use the predictor for binary classification problems of the form: does the label belong to a subset $T \subseteq [k]$: e.g. is this an image of an animal? It ensures that the probabilities predicted by summing the probabilities assigned to labels in $T$ are close to some perfectly calibrated binary predictor for that task. We also show that natural strengthenings of our definition are computationally hard to achieve: they run into information theoretic barriers or computational intractability. Underlying both our upper and lower bounds is a tight connection that we prove between multi-class calibration and the well-studied problem of agnostic learning in the (standard) binary prediction setting.

Omnipredictors for Regression and the Approximate Rank of Convex Functions

Consider the supervised learning setting where the goal is to learn to predict labels $\mathbf y$ given points $\mathbf x$ from a distribution. An \textit{omnipredictor} for a class $\mathcal L$ of loss functions and a class $\mathcal C$ of hypotheses is a predictor whose predictions incur less expected loss than the best hypothesis in $\mathcal C$ for every loss in $\mathcal L$. Since the work of [GKR+21] that introduced the notion, there has been a large body of work in the setting of binary labels where $\mathbf y \in \{0, 1\}$, but much less is known about the regression setting where $\mathbf y \in [0,1]$ can be continuous. Our main conceptual contribution is the notion of \textit{sufficient statistics} for loss minimization over a family of loss functions: these are a set of statistics about a distribution such that knowing them allows one to take actions that minimize the expected loss for any loss in the family. The notion of sufficient statistics relates directly to the approximate rank of the family of loss functions. Our key technical contribution is a bound of $O(1/\varepsilon^{2/3})$ on the $\epsilon$-approximate rank of convex, Lipschitz functions on the interval $[0,1]$, which we show is tight up to a factor of $\mathrm{polylog} (1/\epsilon)$. This yields improved runtimes for learning omnipredictors for the class of all convex, Lipschitz loss functions under weak learnability assumptions about the class $\mathcal C$. We also give efficient omnipredictors when the loss families have low-degree polynomial approximations, or arise from generalized linear models (GLMs). This translation from sufficient statistics to faster omnipredictors is made possible by lifting the technique of loss outcome indistinguishability introduced by [GKH+23] for Boolean labels to the regression setting.

Agnostically Learning Single-Index Models using Omnipredictors

We give the first result for agnostically learning Single-Index Models (SIMs) with arbitrary monotone and Lipschitz activations. All prior work either held only in the realizable setting or required the activation to be known. Moreover, we only require the marginal to have bounded second moments, whereas all prior work required stronger distributional assumptions (such as anticoncentration or boundedness). Our algorithm is based on recent work by [GHK$^+$23] on omniprediction using predictors satisfying calibrated multiaccuracy. Our analysis is simple and relies on the relationship between Bregman divergences (or matching losses) and $\ell_p$ distances. We also provide new guarantees for standard algorithms like GLMtron and logistic regression in the agnostic setting.

When Does Optimizing a Proper Loss Yield Calibration?

Optimizing proper loss functions is popularly believed to yield predictors with good calibration properties; the intuition being that for such losses, the global optimum is to predict the ground-truth probabilities, which is indeed calibrated. However, typical machine learning models are trained to approximately minimize loss over restricted families of predictors, that are unlikely to contain the ground truth. Under what circumstances does optimizing proper loss over a restricted family yield calibrated models? What precise calibration guarantees does it give? In this work, we provide a rigorous answer to these questions. We replace the global optimality with a local optimality condition stipulating that the (proper) loss of the predictor cannot be reduced much by post-processing its predictions with a certain family of Lipschitz functions. We show that any predictor with this local optimality satisfies smooth calibration as defined in Kakade-Foster (2008), B{\l}asiok et al. (2023). Local optimality is plausibly satisfied by well-trained DNNs, which suggests an explanation for why they are calibrated from proper loss minimization alone. Finally, we show that the connection between local optimality and calibration error goes both ways: nearly calibrated predictors are also nearly locally optimal.

Loss minimization yields multicalibration for large neural networks

Multicalibration is a notion of fairness that aims to provide accurate predictions across a large set of groups. Multicalibration is known to be a different goal than loss minimization, even for simple predictors such as linear functions. In this note, we show that for (almost all) large neural network sizes, optimally minimizing squared error leads to multicalibration. Our results are about representational aspects of neural networks, and not about algorithmic or sample complexity considerations. Previous such results were known only for predictors that were nearly Bayes-optimal and were therefore representation independent. We emphasize that our results do not apply to specific algorithms for optimizing neural networks, such as SGD, and they should not be interpreted as "fairness comes for free from optimizing neural networks".