Smooth ECE: Principled Reliability Diagrams via Kernel Smoothing

Calibration measures and reliability diagrams are two fundamental tools for measuring and interpreting the calibration of probabilistic predictors. Calibration measures quantify the degree of miscalibration, and reliability diagrams visualize the structure of this miscalibration. However, the most common constructions of reliability diagrams and calibration measures -- binning and ECE -- both suffer from well-known flaws (e.g. discontinuity). We show that a simple modification fixes both constructions: first smooth the observations using an RBF kernel, then compute the Expected Calibration Error (ECE) of this smoothed function. We prove that with a careful choice of bandwidth, this method yields a calibration measure that is well-behaved in the sense of (B{\l}asiok, Gopalan, Hu, and Nakkiran 2023a) -- a consistent calibration measure. We call this measure the SmoothECE. Moreover, the reliability diagram obtained from this smoothed function visually encodes the SmoothECE, just as binned reliability diagrams encode the BinnedECE. We also provide a Python package with simple, hyperparameter-free methods for measuring and plotting calibration: `pip install relplot\`.

When Does Optimizing a Proper Loss Yield Calibration?

Optimizing proper loss functions is popularly believed to yield predictors with good calibration properties; the intuition being that for such losses, the global optimum is to predict the ground-truth probabilities, which is indeed calibrated. However, typical machine learning models are trained to approximately minimize loss over restricted families of predictors, that are unlikely to contain the ground truth. Under what circumstances does optimizing proper loss over a restricted family yield calibrated models? What precise calibration guarantees does it give? In this work, we provide a rigorous answer to these questions. We replace the global optimality with a local optimality condition stipulating that the (proper) loss of the predictor cannot be reduced much by post-processing its predictions with a certain family of Lipschitz functions. We show that any predictor with this local optimality satisfies smooth calibration as defined in Kakade-Foster (2008), B{\l}asiok et al. (2023). Local optimality is plausibly satisfied by well-trained DNNs, which suggests an explanation for why they are calibrated from proper loss minimization alone. Finally, we show that the connection between local optimality and calibration error goes both ways: nearly calibrated predictors are also nearly locally optimal.

Loss minimization yields multicalibration for large neural networks

Multicalibration is a notion of fairness that aims to provide accurate predictions across a large set of groups. Multicalibration is known to be a different goal than loss minimization, even for simple predictors such as linear functions. In this note, we show that for (almost all) large neural network sizes, optimally minimizing squared error leads to multicalibration. Our results are about representational aspects of neural networks, and not about algorithmic or sample complexity considerations. Previous such results were known only for predictors that were nearly Bayes-optimal and were therefore representation independent. We emphasize that our results do not apply to specific algorithms for optimizing neural networks, such as SGD, and they should not be interpreted as "fairness comes for free from optimizing neural networks".

A Unifying Theory of Distance from Calibration

We study the fundamental question of how to define and measure the distance from calibration for probabilistic predictors. While the notion of perfect calibration is well-understood, there is no consensus on how to quantify the distance from perfect calibration. Numerous calibration measures have been proposed in the literature, but it is unclear how they compare to each other, and many popular measures such as Expected Calibration Error (ECE) fail to satisfy basic properties like continuity. We present a rigorous framework for analyzing calibration measures, inspired by the literature on property testing. We propose a ground-truth notion of distance from calibration: the $\ell_1$ distance to the nearest perfectly calibrated predictor. We define a consistent calibration measure as one that is a polynomial factor approximation to the this distance. Applying our framework, we identify three calibration measures that are consistent and can be estimated efficiently: smooth calibration, interval calibration, and Laplace kernel calibration. The former two give quadratic approximations to the ground truth distance, which we show is information-theoretically optimal. Our work thus establishes fundamental lower and upper bounds on measuring distance to calibration, and also provides theoretical justification for preferring certain metrics (like Laplace kernel calibration) in practice.

What You See is What You Get: Distributional Generalization for Algorithm Design in Deep Learning

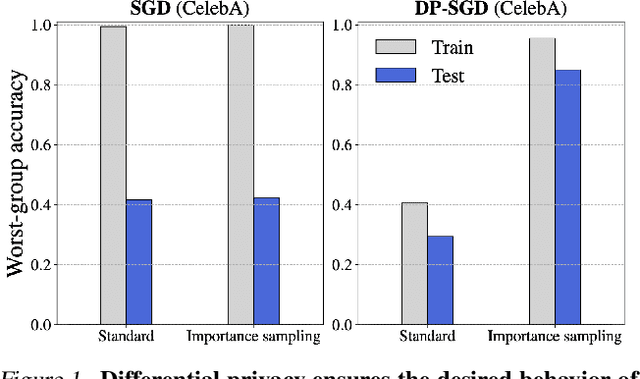
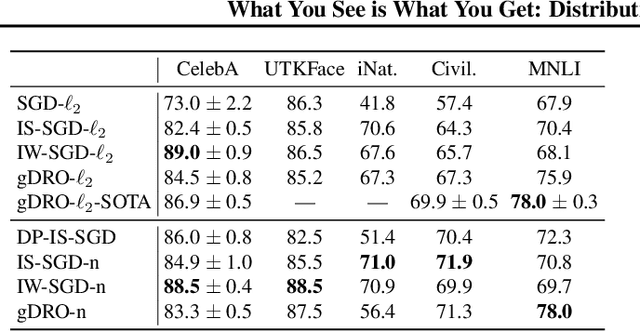
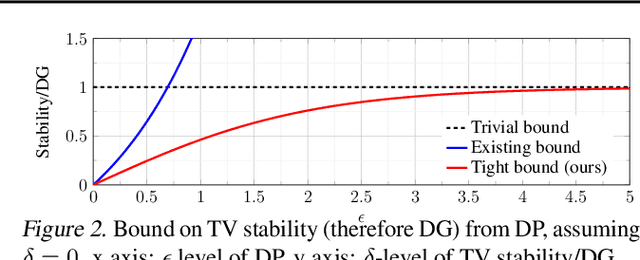
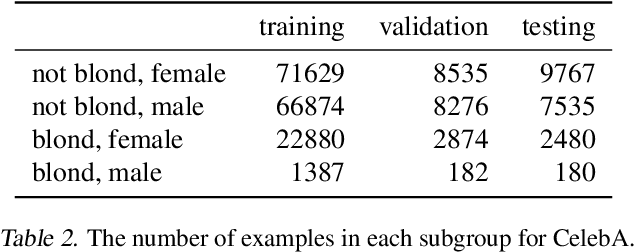
We investigate and leverage a connection between Differential Privacy (DP) and the recently proposed notion of Distributional Generalization (DG). Applying this connection, we introduce new conceptual tools for designing deep-learning methods that bypass "pathologies" of standard stochastic gradient descent (SGD). First, we prove that differentially private methods satisfy a "What You See Is What You Get (WYSIWYG)" generalization guarantee: whatever a model does on its train data is almost exactly what it will do at test time. This guarantee is formally captured by distributional generalization. WYSIWYG enables principled algorithm design in deep learning by reducing $\textit{generalization}$ concerns to $\textit{optimization}$ ones: in order to mitigate unwanted behavior at test time, it is provably sufficient to mitigate this behavior on the train data. This is notably false for standard (non-DP) methods, hence this observation has applications even when privacy is not required. For example, importance sampling is known to fail for standard SGD, but we show that it has exactly the intended effect for DP-trained models. Thus, with DP-SGD, unlike with SGD, we can influence test-time behavior by making principled train-time interventions. We use these insights to construct simple algorithms which match or outperform SOTA in several distributional robustness applications, and to significantly improve the privacy vs. disparate impact trade-off of DP-SGD. Finally, we also improve on known theoretical bounds relating differential privacy, stability, and distributional generalization.

The Generic Holdout: Preventing False-Discoveries in Adaptive Data Science

Adaptive data analysis has posed a challenge to science due to its ability to generate false hypotheses on moderately large data sets. In general, with non-adaptive data analyses (where queries to the data are generated without being influenced by answers to previous queries) a data set containing $n$ samples may support exponentially many queries in $n$. This number reduces to linearly many under naive adaptive data analysis, and even sophisticated remedies such as the Reusable Holdout (Dwork et. al 2015) only allow quadratically many queries in $n$. In this work, we propose a new framework for adaptive science which exponentially improves on this number of queries under a restricted yet scientifically relevant setting, where the goal of the scientist is to find a single (or a few) true hypotheses about the universe based on the samples. Such a setting may describe the search for predictive factors of some disease based on medical data, where the analyst may wish to try a number of predictive models until a satisfactory one is found. Our solution, the Generic Holdout, involves two simple ingredients: (1) a partitioning of the data into a exploration set and a holdout set and (2) a limited exposure strategy for the holdout set. An analyst is free to use the exploration set arbitrarily, but when testing hypotheses against the holdout set, the analyst only learns the answer to the question: "Is the given hypothesis true (empirically) on the holdout set?" -- and no more information, such as "how well" the hypothesis fits the holdout set. The resulting scheme is immediate to analyze, but despite its simplicity we do not believe our method is obvious, as evidenced by the many violations in practice. Our proposal can be seen as an alternative to pre-registration, and allows researchers to get the benefits of adaptive data analysis without the problems of adaptivity.

Predicting Positive and Negative Links with Noisy Queries: Theory & Practice

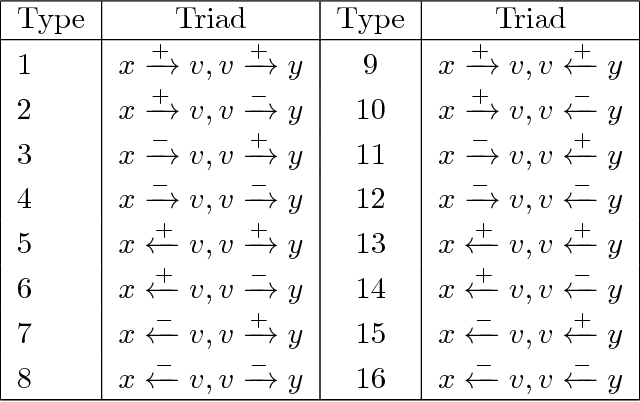
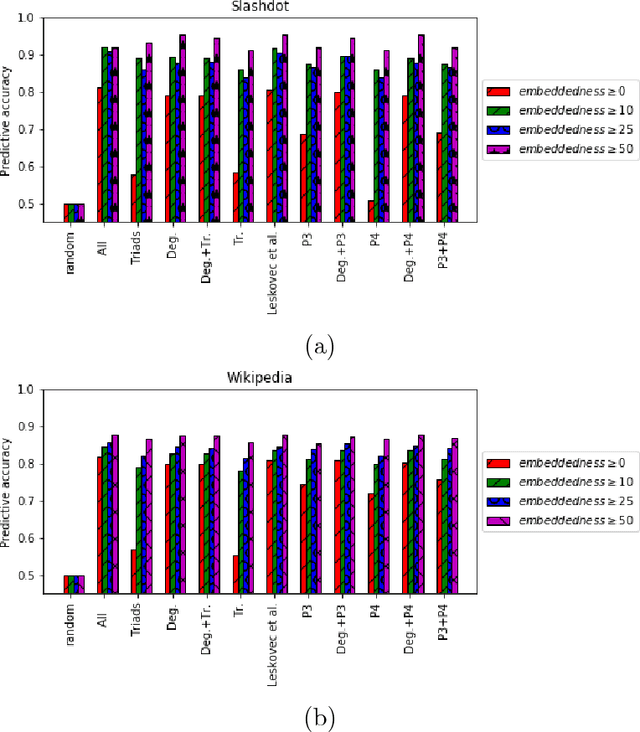
Social networks involve both positive and negative relationships, which can be captured in signed graphs. The {\em edge sign prediction problem} aims to predict whether an interaction between a pair of nodes will be positive or negative. We provide theoretical results for this problem that motivate natural improvements to recent heuristics. The edge sign prediction problem is related to correlation clustering; a positive relationship means being in the same cluster. We consider the following model for two clusters: we are allowed to query any pair of nodes whether they belong to the same cluster or not, but the answer to the query is corrupted with some probability $0<q<\frac{1}{2}$. Let $\delta=1-2q$ be the bias. We provide an algorithm that recovers all signs correctly with high probability in the presence of noise with $O(\frac{n\log n}{\delta^2}+\frac{\log^2 n}{\delta^6})$ queries. This is the best known result for this problem for all but tiny $\delta$, improving on the recent work of Mazumdar and Saha \cite{mazumdar2017clustering}. We also provide an algorithm that performs $O(\frac{n\log n}{\delta^4})$ queries, and uses breadth first search as its main algorithmic primitive. While both the running time and the number of queries for this algorithm are sub-optimal, our result relies on novel theoretical techniques, and naturally suggests the use of edge-disjoint paths as a feature for predicting signs in online social networks. Correspondingly, we experiment with using edge disjoint $s-t$ paths of short length as a feature for predicting the sign of edge $(s,t)$ in real-world signed networks. Empirical findings suggest that the use of such paths improves the classification accuracy, especially for pairs of nodes with no common neighbors.

ADAGIO: Fast Data-aware Near-Isometric Linear Embeddings

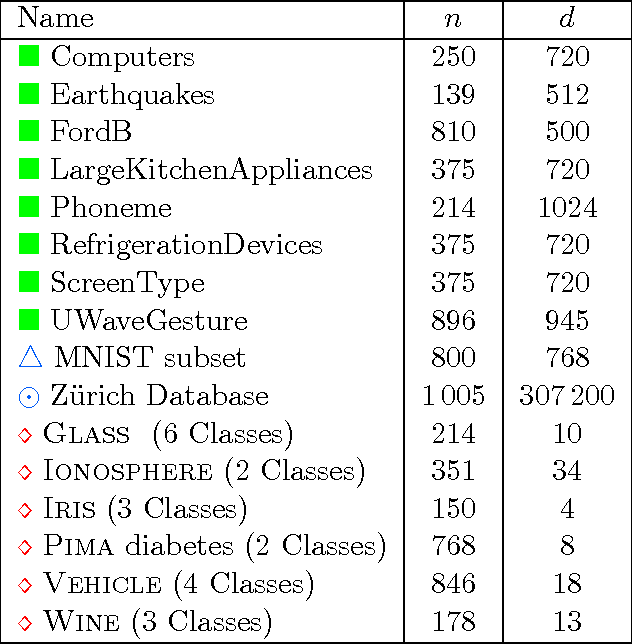
Many important applications, including signal reconstruction, parameter estimation, and signal processing in a compressed domain, rely on a low-dimensional representation of the dataset that preserves {\em all} pairwise distances between the data points and leverages the inherent geometric structure that is typically present. Recently Hedge, Sankaranarayanan, Yin and Baraniuk \cite{hedge2015} proposed the first data-aware near-isometric linear embedding which achieves the best of both worlds. However, their method NuMax does not scale to large-scale datasets. Our main contribution is a simple, data-aware, near-isometric linear dimensionality reduction method which significantly outperforms a state-of-the-art method \cite{hedge2015} with respect to scalability while achieving high quality near-isometries. Furthermore, our method comes with strong worst-case theoretical guarantees that allow us to guarantee the quality of the obtained near-isometry. We verify experimentally the efficiency of our method on numerous real-world datasets, where we find that our method ($<$10 secs) is more than 3\,000$\times$ faster than the state-of-the-art method \cite{hedge2015} ($>$9 hours) on medium scale datasets with 60\,000 data points in 784 dimensions. Finally, we use our method as a preprocessing step to increase the computational efficiency of a classification application and for speeding up approximate nearest neighbor queries.

An improved analysis of the ER-SpUD dictionary learning algorithm

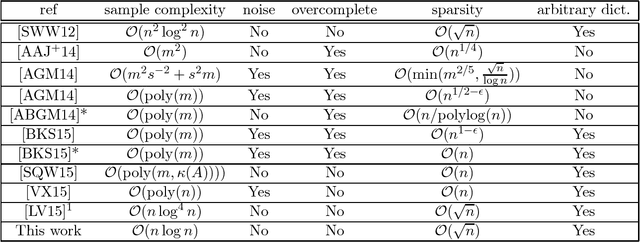
In "dictionary learning" we observe $Y = AX + E$ for some $Y\in\mathbb{R}^{n\times p}$, $A \in\mathbb{R}^{m\times n}$, and $X\in\mathbb{R}^{m\times p}$. The matrix $Y$ is observed, and $A, X, E$ are unknown. Here $E$ is "noise" of small norm, and $X$ is column-wise sparse. The matrix $A$ is referred to as a {\em dictionary}, and its columns as {\em atoms}. Then, given some small number $p$ of samples, i.e.\ columns of $Y$, the goal is to learn the dictionary $A$ up to small error, as well as $X$. The motivation is that in many applications data is expected to sparse when represented by atoms in the "right" dictionary $A$ (e.g.\ images in the Haar wavelet basis), and the goal is to learn $A$ from the data to then use it for other applications. Recently, [SWW12] proposed the dictionary learning algorithm ER-SpUD with provable guarantees when $E = 0$ and $m = n$. They showed if $X$ has independent entries with an expected $s$ non-zeroes per column for $1 \lesssim s \lesssim \sqrt{n}$, and with non-zero entries being subgaussian, then for $p\gtrsim n^2\log^2 n$ with high probability ER-SpUD outputs matrices $A', X'$ which equal $A, X$ up to permuting and scaling columns (resp.\ rows) of $A$ (resp.\ $X$). They conjectured $p\gtrsim n\log n$ suffices, which they showed was information theoretically necessary for {\em any} algorithm to succeed when $s \simeq 1$. Significant progress was later obtained in [LV15]. We show that for a slight variant of ER-SpUD, $p\gtrsim n\log(n/\delta)$ samples suffice for successful recovery with probability $1-\delta$. We also show that for the unmodified ER-SpUD, $p\gtrsim n^{1.99}$ samples are required even to learn $A, X$ with polynomially small success probability. This resolves the main conjecture of [SWW12], and contradicts the main result of [LV15], which claimed that $p\gtrsim n\log^4 n$ guarantees success whp.