Efficient and Provable Algorithms for Covariate Shift

Covariate shift, a widely used assumption in tackling {\it distributional shift} (when training and test distributions differ), focuses on scenarios where the distribution of the labels conditioned on the feature vector is the same, but the distribution of features in the training and test data are different. Despite the significance and extensive work on covariate shift, theoretical guarantees for algorithms in this domain remain sparse. In this paper, we distill the essence of the covariate shift problem and focus on estimating the average $\mathbb{E}_{\tilde{\mathbf{x}}\sim p_{\mathrm{test}}}\mathbf{f}(\tilde{\mathbf{x}})$, of any unknown and bounded function $\mathbf{f}$, given labeled training samples $(\mathbf{x}_i, \mathbf{f}(\mathbf{x}_i))$, and unlabeled test samples $\tilde{\mathbf{x}}_i$; this is a core subroutine for several widely studied learning problems. We give several efficient algorithms, with provable sample complexity and computational guarantees. Moreover, we provide the first rigorous analysis of algorithms in this space when $\mathbf{f}$ is unrestricted, laying the groundwork for developing a solid theoretical foundation for covariate shift problems.

Fast, Provably convergent IRLS Algorithm for p-norm Linear Regression

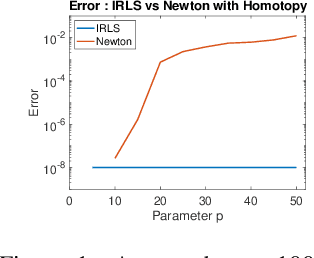
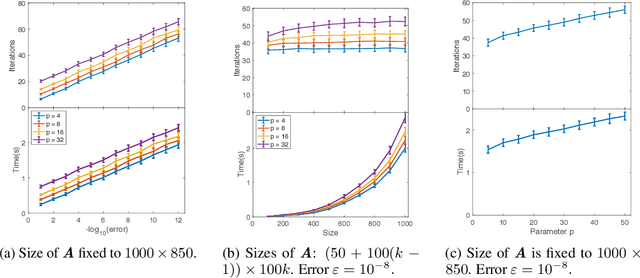
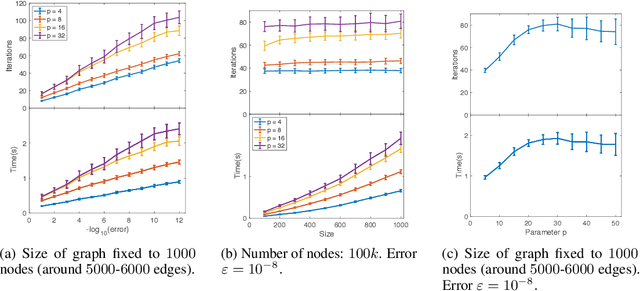
Linear regression in $\ell_p$-norm is a canonical optimization problem that arises in several applications, including sparse recovery, semi-supervised learning, and signal processing. Generic convex optimization algorithms for solving $\ell_p$-regression are slow in practice. Iteratively Reweighted Least Squares (IRLS) is an easy to implement family of algorithms for solving these problems that has been studied for over 50 years. However, these algorithms often diverge for p > 3, and since the work of Osborne (1985), it has been an open problem whether there is an IRLS algorithm that is guaranteed to converge rapidly for p > 3. We propose p-IRLS, the first IRLS algorithm that provably converges geometrically for any $p \in [2,\infty).$ Our algorithm is simple to implement and is guaranteed to find a $(1+\varepsilon)$-approximate solution in $O(p^{3.5} m^{\frac{p-2}{2(p-1)}} \log \frac{m}{\varepsilon}) \le O_p(\sqrt{m} \log \frac{m}{\varepsilon} )$ iterations. Our experiments demonstrate that it performs even better than our theoretical bounds, beats the standard Matlab/CVX implementation for solving these problems by 10--50x, and is the fastest among available implementations in the high-accuracy regime.

Iterative Refinement for $\ell_p$-norm Regression

We give improved algorithms for the $\ell_{p}$-regression problem, $\min_{x} \|x\|_{p}$ such that $A x=b,$ for all $p \in (1,2) \cup (2,\infty).$ Our algorithms obtain a high accuracy solution in $\tilde{O}_{p}(m^{\frac{|p-2|}{2p + |p-2|}}) \le \tilde{O}_{p}(m^{\frac{1}{3}})$ iterations, where each iteration requires solving an $m \times m$ linear system, $m$ being the dimension of the ambient space. By maintaining an approximate inverse of the linear systems that we solve in each iteration, we give algorithms for solving $\ell_{p}$-regression to $1 / \text{poly}(n)$ accuracy that run in time $\tilde{O}_p(m^{\max\{\omega, 7/3\}}),$ where $\omega$ is the matrix multiplication constant. For the current best value of $\omega > 2.37$, we can thus solve $\ell_{p}$ regression as fast as $\ell_{2}$ regression, for all constant $p$ bounded away from $1.$ Our algorithms can be combined with fast graph Laplacian linear equation solvers to give minimum $\ell_{p}$-norm flow / voltage solutions to $1 / \text{poly}(n)$ accuracy on an undirected graph with $m$ edges in $\tilde{O}_{p}(m^{1 + \frac{|p-2|}{2p + |p-2|}}) \le \tilde{O}_{p}(m^{\frac{4}{3}})$ time. For sparse graphs and for matrices with similar dimensions, our iteration counts and running times improve on the $p$-norm regression algorithm by [Bubeck-Cohen-Lee-Li STOC`18] and general-purpose convex optimization algorithms. At the core of our algorithms is an iterative refinement scheme for $\ell_{p}$-norms, using the smoothed $\ell_{p}$-norms introduced in the work of Bubeck et al. Given an initial solution, we construct a problem that seeks to minimize a quadratically-smoothed $\ell_{p}$ norm over a subspace, such that a crude solution to this problem allows us to improve the initial solution by a constant factor, leading to algorithms with fast convergence.