Assessing GPT Performance in a Proof-Based University-Level Course Under Blind Grading

As large language models (LLMs) advance, their role in higher education, particularly in free-response problem-solving, requires careful examination. This study assesses the performance of GPT-4o and o1-preview under realistic educational conditions in an undergraduate algorithms course. Anonymous GPT-generated solutions to take-home exams were graded by teaching assistants unaware of their origin. Our analysis examines both coarse-grained performance (scores) and fine-grained reasoning quality (error patterns). Results show that GPT-4o consistently struggles, failing to reach the passing threshold, while o1-preview performs significantly better, surpassing the passing score and even exceeding the student median in certain exercises. However, both models exhibit issues with unjustified claims and misleading arguments. These findings highlight the need for robust assessment strategies and AI-aware grading policies in education.

On the Oracle Complexity of Higher-Order Smooth Non-Convex Finite-Sum Optimization

We prove lower bounds for higher-order methods in smooth non-convex finite-sum optimization. Our contribution is threefold: We first show that a deterministic algorithm cannot profit from the finite-sum structure of the objective, and that simulating a pth-order regularized method on the whole function by constructing exact gradient information is optimal up to constant factors. We further show lower bounds for randomized algorithms and compare them with the best known upper bounds. To address some gaps between the bounds, we propose a new second-order smoothness assumption that can be seen as an analogue of the first-order mean-squared smoothness assumption. We prove that it is sufficient to ensure state-of-the-art convergence guarantees, while allowing for a sharper lower bound.

Iterative Refinement for $\ell_p$-norm Regression

We give improved algorithms for the $\ell_{p}$-regression problem, $\min_{x} \|x\|_{p}$ such that $A x=b,$ for all $p \in (1,2) \cup (2,\infty).$ Our algorithms obtain a high accuracy solution in $\tilde{O}_{p}(m^{\frac{|p-2|}{2p + |p-2|}}) \le \tilde{O}_{p}(m^{\frac{1}{3}})$ iterations, where each iteration requires solving an $m \times m$ linear system, $m$ being the dimension of the ambient space. By maintaining an approximate inverse of the linear systems that we solve in each iteration, we give algorithms for solving $\ell_{p}$-regression to $1 / \text{poly}(n)$ accuracy that run in time $\tilde{O}_p(m^{\max\{\omega, 7/3\}}),$ where $\omega$ is the matrix multiplication constant. For the current best value of $\omega > 2.37$, we can thus solve $\ell_{p}$ regression as fast as $\ell_{2}$ regression, for all constant $p$ bounded away from $1.$ Our algorithms can be combined with fast graph Laplacian linear equation solvers to give minimum $\ell_{p}$-norm flow / voltage solutions to $1 / \text{poly}(n)$ accuracy on an undirected graph with $m$ edges in $\tilde{O}_{p}(m^{1 + \frac{|p-2|}{2p + |p-2|}}) \le \tilde{O}_{p}(m^{\frac{4}{3}})$ time. For sparse graphs and for matrices with similar dimensions, our iteration counts and running times improve on the $p$-norm regression algorithm by [Bubeck-Cohen-Lee-Li STOC`18] and general-purpose convex optimization algorithms. At the core of our algorithms is an iterative refinement scheme for $\ell_{p}$-norms, using the smoothed $\ell_{p}$-norms introduced in the work of Bubeck et al. Given an initial solution, we construct a problem that seeks to minimize a quadratically-smoothed $\ell_{p}$ norm over a subspace, such that a crude solution to this problem allows us to improve the initial solution by a constant factor, leading to algorithms with fast convergence.

Fast, Provable Algorithms for Isotonic Regression in all $\ell_{p}$-norms

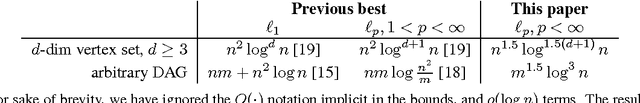
Given a directed acyclic graph $G,$ and a set of values $y$ on the vertices, the Isotonic Regression of $y$ is a vector $x$ that respects the partial order described by $G,$ and minimizes $||x-y||,$ for a specified norm. This paper gives improved algorithms for computing the Isotonic Regression for all weighted $\ell_{p}$-norms with rigorous performance guarantees. Our algorithms are quite practical, and their variants can be implemented to run fast in practice.

Algorithms for Lipschitz Learning on Graphs

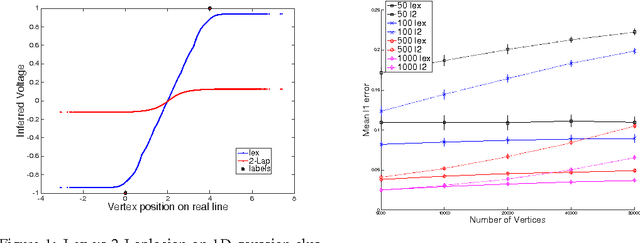
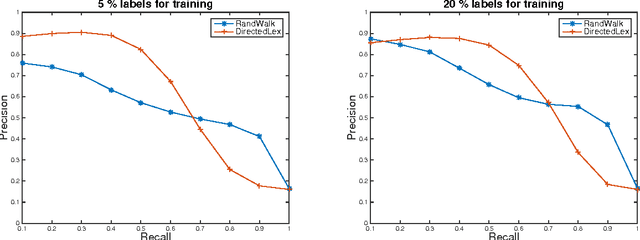
We develop fast algorithms for solving regression problems on graphs where one is given the value of a function at some vertices, and must find its smoothest possible extension to all vertices. The extension we compute is the absolutely minimal Lipschitz extension, and is the limit for large $p$ of $p$-Laplacian regularization. We present an algorithm that computes a minimal Lipschitz extension in expected linear time, and an algorithm that computes an absolutely minimal Lipschitz extension in expected time $\widetilde{O} (m n)$. The latter algorithm has variants that seem to run much faster in practice. These extensions are particularly amenable to regularization: we can perform $l_{0}$-regularization on the given values in polynomial time and $l_{1}$-regularization on the initial function values and on graph edge weights in time $\widetilde{O} (m^{3/2})$.