Daniel A. Spielman
Algorithms for Lipschitz Learning on Graphs
Jun 30, 2015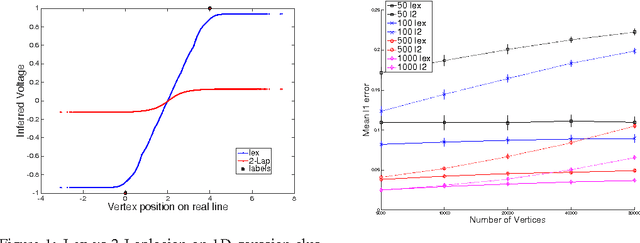
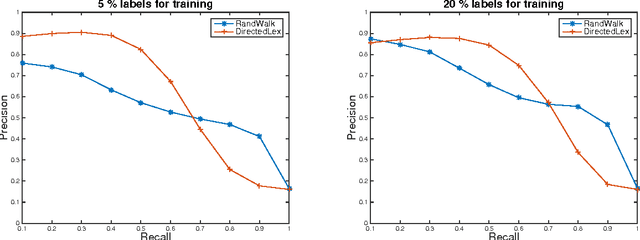
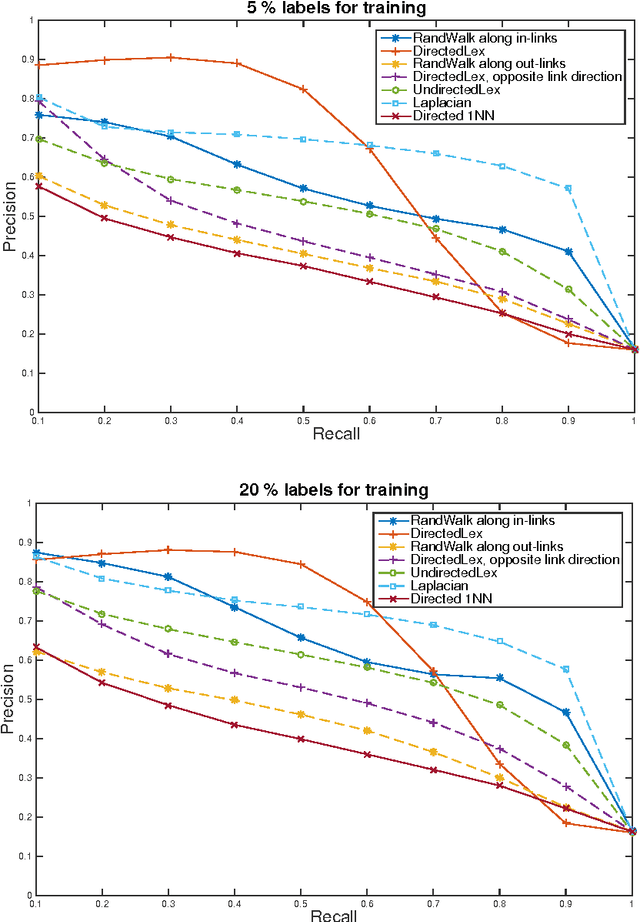
Abstract:We develop fast algorithms for solving regression problems on graphs where one is given the value of a function at some vertices, and must find its smoothest possible extension to all vertices. The extension we compute is the absolutely minimal Lipschitz extension, and is the limit for large $p$ of $p$-Laplacian regularization. We present an algorithm that computes a minimal Lipschitz extension in expected linear time, and an algorithm that computes an absolutely minimal Lipschitz extension in expected time $\widetilde{O} (m n)$. The latter algorithm has variants that seem to run much faster in practice. These extensions are particularly amenable to regularization: we can perform $l_{0}$-regularization on the given values in polynomial time and $l_{1}$-regularization on the initial function values and on graph edge weights in time $\widetilde{O} (m^{3/2})$.
Exact Recovery of Sparsely-Used Dictionaries
Jun 26, 2012
Abstract:We consider the problem of learning sparsely used dictionaries with an arbitrary square dictionary and a random, sparse coefficient matrix. We prove that $O (n \log n)$ samples are sufficient to uniquely determine the coefficient matrix. Based on this proof, we design a polynomial-time algorithm, called Exact Recovery of Sparsely-Used Dictionaries (ER-SpUD), and prove that it probably recovers the dictionary and coefficient matrix when the coefficient matrix is sufficiently sparse. Simulation results show that ER-SpUD reveals the true dictionary as well as the coefficients with probability higher than many state-of-the-art algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge