Anup Rao
Learning to Reason in LLMs by Expectation Maximization
Dec 23, 2025

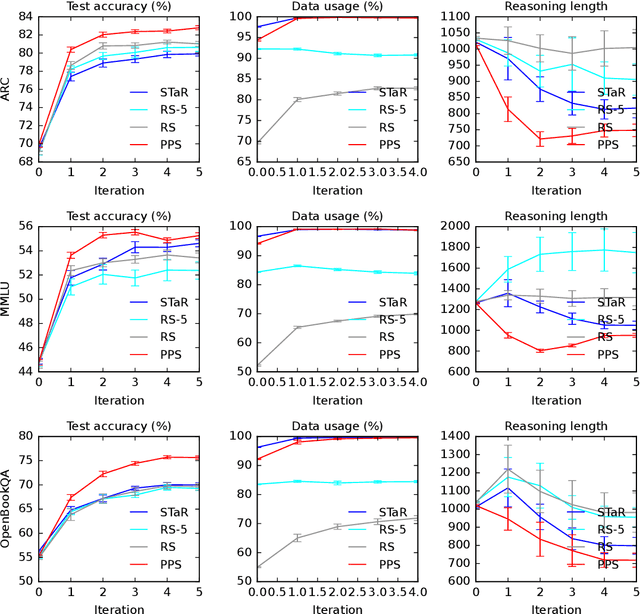
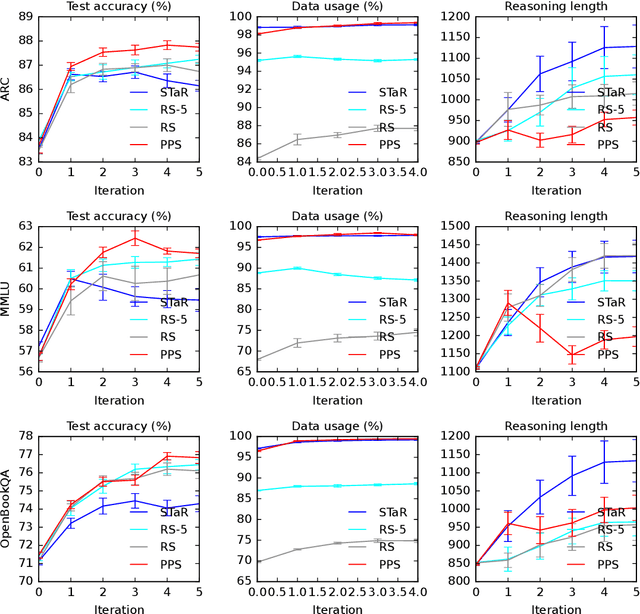
Abstract:Large language models (LLMs) solve reasoning problems by first generating a rationale and then answering. We formalize reasoning as a latent variable model and derive an expectation-maximization (EM) objective for learning to reason. This view connects EM and modern reward-based optimization, and shows that the main challenge lies in designing a sampling distribution that generates rationales that justify correct answers. We instantiate and compare several sampling schemes: rejection sampling with a budget, self-taught reasoner (STaR), and prompt posterior sampling (PPS), which only keeps the rationalization stage of STaR. Our experiments on the ARC, MMLU, and OpenBookQA datasets with the Llama and Qwen models show that the sampling scheme can significantly affect the accuracy of learned reasoning models. Despite its simplicity, we observe that PPS outperforms the other sampling schemes.
Learning to Clarify by Reinforcement Learning Through Reward-Weighted Fine-Tuning
Jun 08, 2025


Abstract:Question answering (QA) agents automatically answer questions posed in natural language. In this work, we learn to ask clarifying questions in QA agents. The key idea in our method is to simulate conversations that contain clarifying questions and learn from them using reinforcement learning (RL). To make RL practical, we propose and analyze offline RL objectives that can be viewed as reward-weighted supervised fine-tuning (SFT) and easily optimized in large language models. Our work stands in a stark contrast to recently proposed methods, based on SFT and direct preference optimization, which have additional hyper-parameters and do not directly optimize rewards. We compare to these methods empirically and report gains in both optimized rewards and language quality.
Evaluation and Incident Prevention in an Enterprise AI Assistant
Apr 11, 2025



Abstract:Enterprise AI Assistants are increasingly deployed in domains where accuracy is paramount, making each erroneous output a potentially significant incident. This paper presents a comprehensive framework for monitoring, benchmarking, and continuously improving such complex, multi-component systems under active development by multiple teams. Our approach encompasses three key elements: (1) a hierarchical ``severity'' framework for incident detection that identifies and categorizes errors while attributing component-specific error rates, facilitating targeted improvements; (2) a scalable and principled methodology for benchmark construction, evaluation, and deployment, designed to accommodate multiple development teams, mitigate overfitting risks, and assess the downstream impact of system modifications; and (3) a continual improvement strategy leveraging multidimensional evaluation, enabling the identification and implementation of diverse enhancement opportunities. By adopting this holistic framework, organizations can systematically enhance the reliability and performance of their AI Assistants, ensuring their efficacy in critical enterprise environments. We conclude by discussing how this multifaceted evaluation approach opens avenues for various classes of enhancements, paving the way for more robust and trustworthy AI systems.
Hallucination Diversity-Aware Active Learning for Text Summarization
Apr 02, 2024



Abstract:Large Language Models (LLMs) have shown propensity to generate hallucinated outputs, i.e., texts that are factually incorrect or unsupported. Existing methods for alleviating hallucinations typically require costly human annotations to identify and correct hallucinations in LLM outputs. Moreover, most of these methods focus on a specific type of hallucination, e.g., entity or token errors, which limits their effectiveness in addressing various types of hallucinations exhibited in LLM outputs. To our best knowledge, in this paper we propose the first active learning framework to alleviate LLM hallucinations, reducing costly human annotations of hallucination needed. By measuring fine-grained hallucinations from errors in semantic frame, discourse and content verifiability in text summarization, we propose HAllucination Diversity-Aware Sampling (HADAS) to select diverse hallucinations for annotations in active learning for LLM finetuning. Extensive experiments on three datasets and different backbone models demonstrate advantages of our method in effectively and efficiently mitigating LLM hallucinations.
Decentralized Personalized Online Federated Learning
Nov 08, 2023Abstract:Vanilla federated learning does not support learning in an online environment, learning a personalized model on each client, and learning in a decentralized setting. There are existing methods extending federated learning in each of the three aspects. However, some important applications on enterprise edge servers (e.g. online item recommendation at global scale) involve the three aspects at the same time. Therefore, we propose a new learning setting \textit{Decentralized Personalized Online Federated Learning} that considers all the three aspects at the same time. In this new setting for learning, the first technical challenge is how to aggregate the shared model parameters from neighboring clients to obtain a personalized local model with good performance on each client. We propose to directly learn an aggregation by optimizing the performance of the local model with respect to the aggregation weights. This not only improves personalization of each local model but also helps the local model adapting to potential data shift by intelligently incorporating the right amount of information from its neighbors. The second challenge is how to select the neighbors for each client. We propose a peer selection method based on the learned aggregation weights enabling each client to select the most helpful neighbors and reduce communication cost at the same time. We verify the effectiveness and robustness of our proposed method on three real-world item recommendation datasets and one air quality prediction dataset.
Sample Constrained Treatment Effect Estimation
Oct 12, 2022



Abstract:Treatment effect estimation is a fundamental problem in causal inference. We focus on designing efficient randomized controlled trials, to accurately estimate the effect of some treatment on a population of $n$ individuals. In particular, we study sample-constrained treatment effect estimation, where we must select a subset of $s \ll n$ individuals from the population to experiment on. This subset must be further partitioned into treatment and control groups. Algorithms for partitioning the entire population into treatment and control groups, or for choosing a single representative subset, have been well-studied. The key challenge in our setting is jointly choosing a representative subset and a partition for that set. We focus on both individual and average treatment effect estimation, under a linear effects model. We give provably efficient experimental designs and corresponding estimators, by identifying connections to discrepancy minimization and leverage-score-based sampling used in randomized numerical linear algebra. Our theoretical results obtain a smooth transition to known guarantees when $s$ equals the population size. We also empirically demonstrate the performance of our algorithms.
Electra: Conditional Generative Model based Predicate-Aware Query Approximation
Jan 28, 2022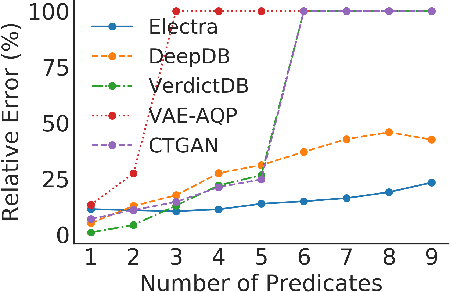
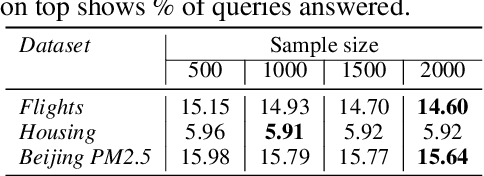
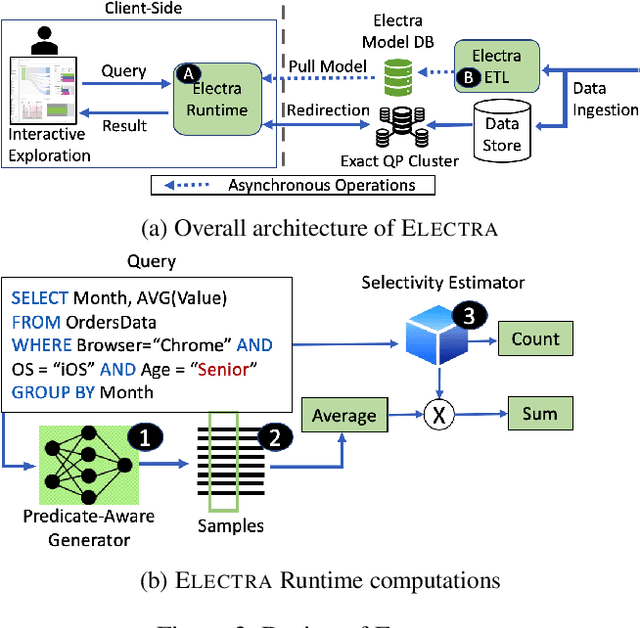
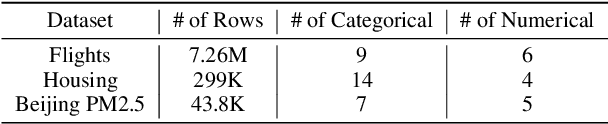
Abstract:The goal of Approximate Query Processing (AQP) is to provide very fast but "accurate enough" results for costly aggregate queries thereby improving user experience in interactive exploration of large datasets. Recently proposed Machine-Learning based AQP techniques can provide very low latency as query execution only involves model inference as compared to traditional query processing on database clusters. However, with increase in the number of filtering predicates(WHERE clauses), the approximation error significantly increases for these methods. Analysts often use queries with a large number of predicates for insights discovery. Thus, maintaining low approximation error is important to prevent analysts from drawing misleading conclusions. In this paper, we propose ELECTRA, a predicate-aware AQP system that can answer analytics-style queries with a large number of predicates with much smaller approximation errors. ELECTRA uses a conditional generative model that learns the conditional distribution of the data and at runtime generates a small (~1000 rows) but representative sample, on which the query is executed to compute the approximate result. Our evaluations with four different baselines on three real-world datasets show that ELECTRA provides lower AQP error for large number of predicates compared to baselines.
Online MAP Inference and Learning for Nonsymmetric Determinantal Point Processes
Nov 29, 2021
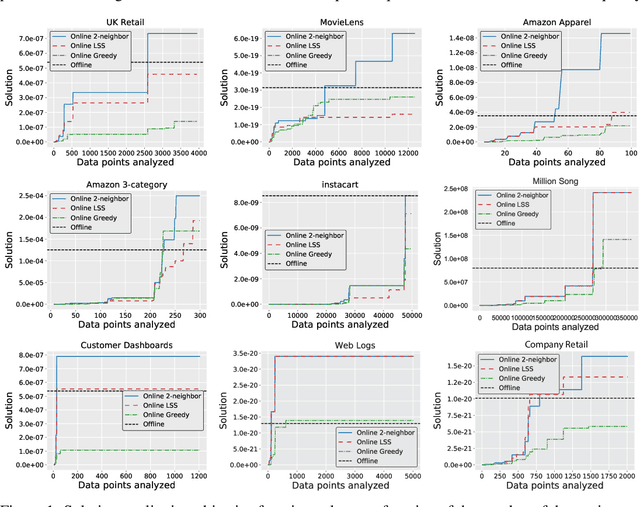
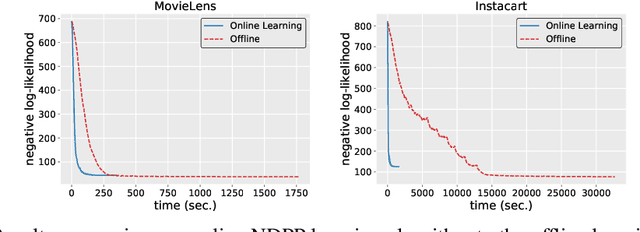
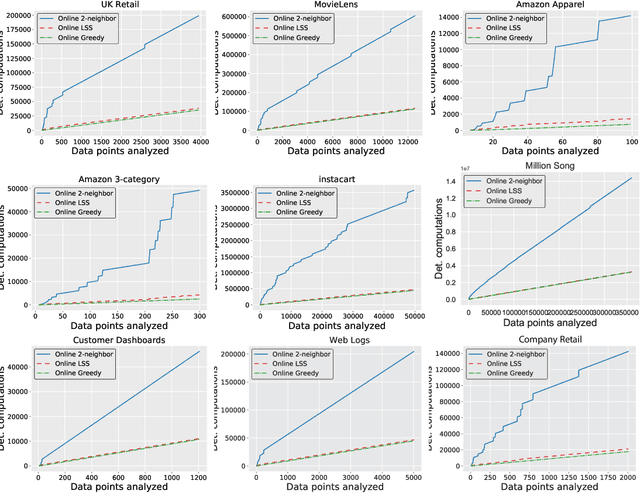
Abstract:In this paper, we introduce the online and streaming MAP inference and learning problems for Non-symmetric Determinantal Point Processes (NDPPs) where data points arrive in an arbitrary order and the algorithms are constrained to use a single-pass over the data as well as sub-linear memory. The online setting has an additional requirement of maintaining a valid solution at any point in time. For solving these new problems, we propose algorithms with theoretical guarantees, evaluate them on several real-world datasets, and show that they give comparable performance to state-of-the-art offline algorithms that store the entire data in memory and take multiple passes over it.
An Interpretable Graph Generative Model with Heterophily
Nov 04, 2021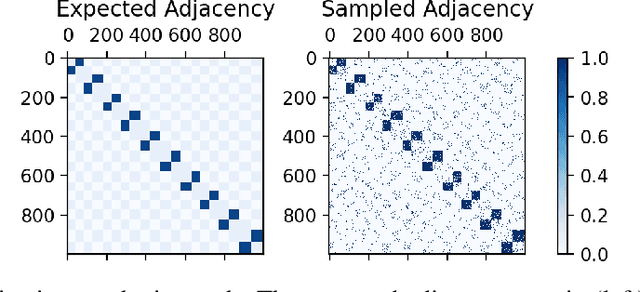
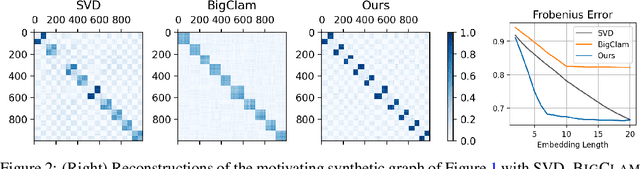
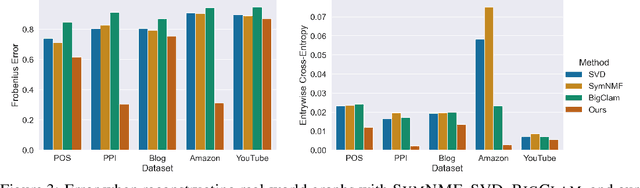
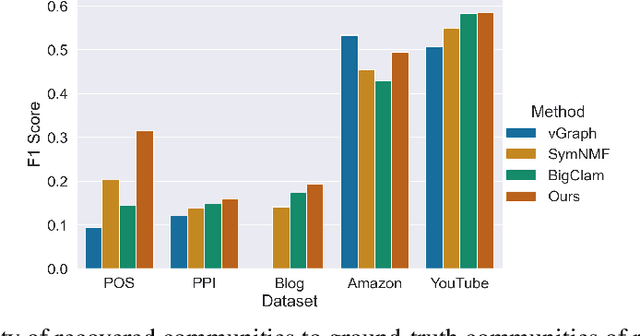
Abstract:Many models for graphs fall under the framework of edge-independent dot product models. These models output the probabilities of edges existing between all pairs of nodes, and the probability of a link between two nodes increases with the dot product of vectors associated with the nodes. Recent work has shown that these models are unable to capture key structures in real-world graphs, particularly heterophilous structures, wherein links occur between dissimilar nodes. We propose the first edge-independent graph generative model that is a) expressive enough to capture heterophily, b) produces nonnegative embeddings, which allow link predictions to be interpreted in terms of communities, and c) optimizes effectively on real-world graphs with gradient descent on a cross-entropy loss. Our theoretical results demonstrate the expressiveness of our model in its ability to exactly reconstruct a graph using a number of clusters that is linear in the maximum degree, along with its ability to capture both heterophily and homophily in the data. Further, our experiments demonstrate the effectiveness of our model for a variety of important application tasks such as multi-label clustering and link prediction.
Multiscale Manifold Warping
Sep 19, 2021
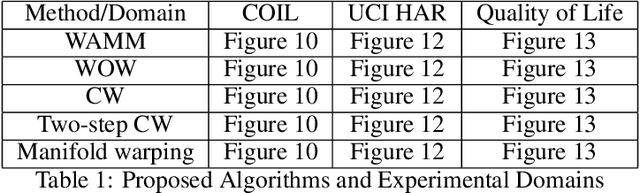

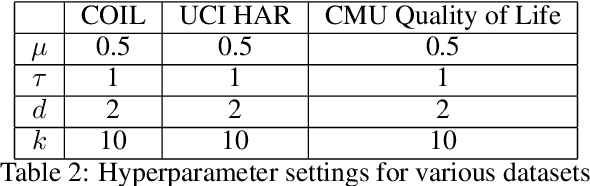
Abstract:Many real-world applications require aligning two temporal sequences, including bioinformatics, handwriting recognition, activity recognition, and human-robot coordination. Dynamic Time Warping (DTW) is a popular alignment method, but can fail on high-dimensional real-world data where the dimensions of aligned sequences are often unequal. In this paper, we show that exploiting the multiscale manifold latent structure of real-world data can yield improved alignment. We introduce a novel framework called Warping on Wavelets (WOW) that integrates DTW with a a multi-scale manifold learning framework called Diffusion Wavelets. We present a theoretical analysis of the WOW family of algorithms and show that it outperforms previous state of the art methods, such as canonical time warping (CTW) and manifold warping, on several real-world datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge