Kernel Methods and Multi-layer Perceptrons Learn Linear Models in High Dimensions

Empirical observation of high dimensional phenomena, such as the double descent behaviour, has attracted a lot of interest in understanding classical techniques such as kernel methods, and their implications to explain generalization properties of neural networks. Many recent works analyze such models in a certain high-dimensional regime where the covariates are independent and the number of samples and the number of covariates grow at a fixed ratio (i.e. proportional asymptotics). In this work we show that for a large class of kernels, including the neural tangent kernel of fully connected networks, kernel methods can only perform as well as linear models in this regime. More surprisingly, when the data is generated by a kernel model where the relationship between input and the response could be very nonlinear, we show that linear models are in fact optimal, i.e. linear models achieve the minimum risk among all models, linear or nonlinear. These results suggest that more complex models for the data other than independent features are needed for high-dimensional analysis.

Asymptotics of Ridge Regression in Convolutional Models

Understanding generalization and estimation error of estimators for simple models such as linear and generalized linear models has attracted a lot of attention recently. This is in part due to an interesting observation made in machine learning community that highly over-parameterized neural networks achieve zero training error, and yet they are able to generalize well over the test samples. This phenomenon is captured by the so called double descent curve, where the generalization error starts decreasing again after the interpolation threshold. A series of recent works tried to explain such phenomenon for simple models. In this work, we analyze the asymptotics of estimation error in ridge estimators for convolutional linear models. These convolutional inverse problems, also known as deconvolution, naturally arise in different fields such as seismology, imaging, and acoustics among others. Our results hold for a large class of input distributions that include i.i.d. features as a special case. We derive exact formulae for estimation error of ridge estimators that hold in a certain high-dimensional regime. We show the double descent phenomenon in our experiments for convolutional models and show that our theoretical results match the experiments.

Implicit Bias of Linear RNNs

Contemporary wisdom based on empirical studies suggests that standard recurrent neural networks (RNNs) do not perform well on tasks requiring long-term memory. However, precise reasoning for this behavior is still unknown. This paper provides a rigorous explanation of this property in the special case of linear RNNs. Although this work is limited to linear RNNs, even these systems have traditionally been difficult to analyze due to their non-linear parameterization. Using recently-developed kernel regime analysis, our main result shows that linear RNNs learned from random initializations are functionally equivalent to a certain weighted 1D-convolutional network. Importantly, the weightings in the equivalent model cause an implicit bias to elements with smaller time lags in the convolution and hence, shorter memory. The degree of this bias depends on the variance of the transition kernel matrix at initialization and is related to the classic exploding and vanishing gradients problem. The theory is validated in both synthetic and real data experiments.

Low-Rank Nonlinear Decoding of $μ$-ECoG from the Primary Auditory Cortex

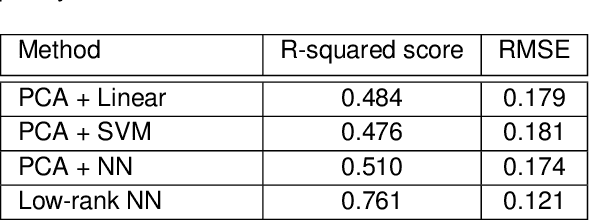
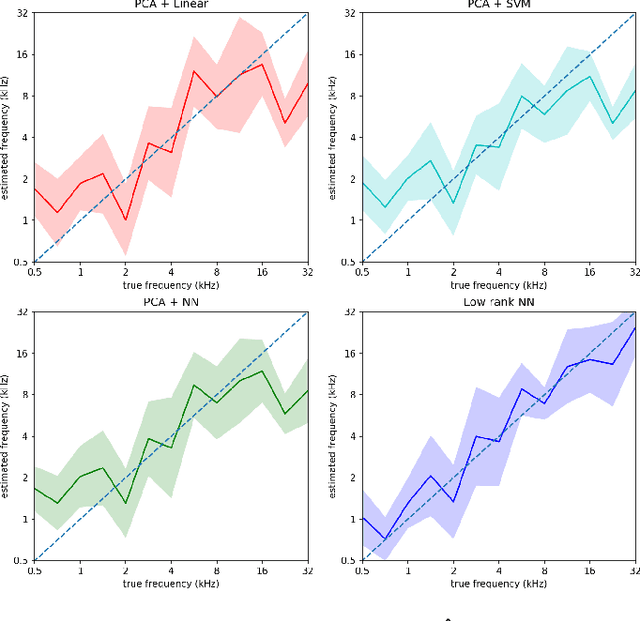
This paper considers the problem of neural decoding from parallel neural measurements systems such as micro-electrocorticography ($\mu$-ECoG). In systems with large numbers of array elements at very high sampling rates, the dimension of the raw measurement data may be large. Learning neural decoders for this high-dimensional data can be challenging, particularly when the number of training samples is limited. To address this challenge, this work presents a novel neural network decoder with a low-rank structure in the first hidden layer. The low-rank constraints dramatically reduce the number of parameters in the decoder while still enabling a rich class of nonlinear decoder maps. The low-rank decoder is illustrated on $\mu$-ECoG data from the primary auditory cortex (A1) of awake rats. This decoding problem is particularly challenging due to the complexity of neural responses in the auditory cortex and the presence of confounding signals in awake animals. It is shown that the proposed low-rank decoder significantly outperforms models using standard dimensionality reduction techniques such as principal component analysis (PCA).

Generalization Error of Generalized Linear Models in High Dimensions

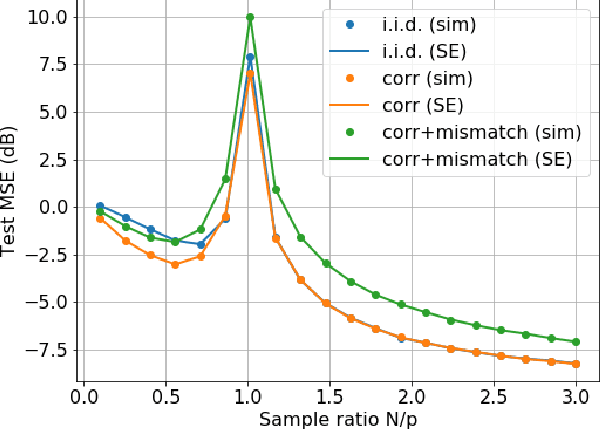
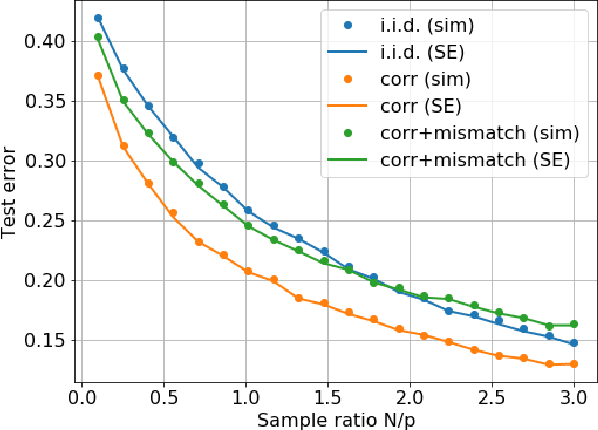
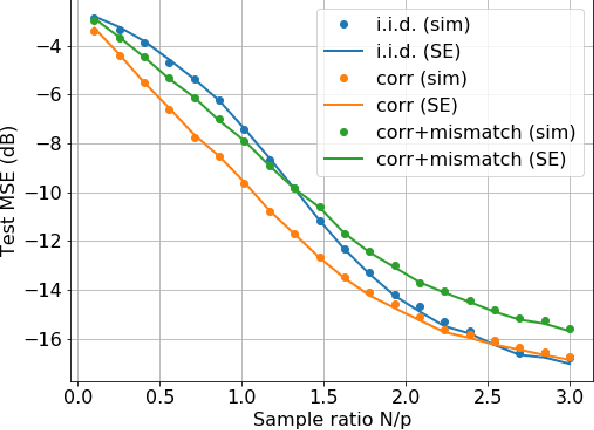
At the heart of machine learning lies the question of generalizability of learned rules over previously unseen data. While over-parameterized models based on neural networks are now ubiquitous in machine learning applications, our understanding of their generalization capabilities is incomplete. This task is made harder by the non-convexity of the underlying learning problems. We provide a general framework to characterize the asymptotic generalization error for single-layer neural networks (i.e., generalized linear models) with arbitrary non-linearities, making it applicable to regression as well as classification problems. This framework enables analyzing the effect of (i) over-parameterization and non-linearity during modeling; and (ii) choices of loss function, initialization, and regularizer during learning. Our model also captures mismatch between training and test distributions. As examples, we analyze a few special cases, namely linear regression and logistic regression. We are also able to rigorously and analytically explain the \emph{double descent} phenomenon in generalized linear models.

Inference in Multi-Layer Networks with Matrix-Valued Unknowns

We consider the problem of inferring the input and hidden variables of a stochastic multi-layer neural network from an observation of the output. The hidden variables in each layer are represented as matrices. This problem applies to signal recovery via deep generative prior models, multi-task and mixed regression and learning certain classes of two-layer neural networks. A unified approximation algorithm for both MAP and MMSE inference is proposed by extending a recently-developed Multi-Layer Vector Approximate Message Passing (ML-VAMP) algorithm to handle matrix-valued unknowns. It is shown that the performance of the proposed Multi-Layer Matrix VAMP (ML-Mat-VAMP) algorithm can be exactly predicted in a certain random large-system limit, where the dimensions $N\times d$ of the unknown quantities grow as $N\rightarrow\infty$ with $d$ fixed. In the two-layer neural-network learning problem, this scaling corresponds to the case where the number of input features and training samples grow to infinity but the number of hidden nodes stays fixed. The analysis enables a precise prediction of the parameter and test error of the learning.

Inference with Deep Generative Priors in High Dimensions

Deep generative priors offer powerful models for complex-structured data, such as images, audio, and text. Using these priors in inverse problems typically requires estimating the input and/or hidden signals in a multi-layer deep neural network from observation of its output. While these approaches have been successful in practice, rigorous performance analysis is complicated by the non-convex nature of the underlying optimization problems. This paper presents a novel algorithm, Multi-Layer Vector Approximate Message Passing (ML-VAMP), for inference in multi-layer stochastic neural networks. ML-VAMP can be configured to compute maximum a priori (MAP) or approximate minimum mean-squared error (MMSE) estimates for these networks. We show that the performance of ML-VAMP can be exactly predicted in a certain high-dimensional random limit. Furthermore, under certain conditions, ML-VAMP yields estimates that achieve the minimum (i.e., Bayes-optimal) MSE as predicted by the replica method. In this way, ML-VAMP provides a computationally efficient method for multi-layer inference with an exact performance characterization and testable conditions for optimality in the large-system limit.

High-Dimensional Bernoulli Autoregressive Process with Long-Range Dependence

We consider the problem of estimating the parameters of a multivariate Bernoulli process with auto-regressive feedback in the high-dimensional setting where the number of samples available is much less than the number of parameters. This problem arises in learning interconnections of networks of dynamical systems with spiking or binary-valued data. We allow the process to depend on its past up to a lag $p$, for a general $p \ge 1$, allowing for more realistic modeling in many applications. We propose and analyze an $\ell_1$-regularized maximum likelihood estimator (MLE) under the assumption that the parameter tensor is approximately sparse. Rigorous analysis of such estimators is made challenging by the dependent and non-Gaussian nature of the process as well as the presence of the nonlinearities and multi-level feedback. We derive precise upper bounds on the mean-squared estimation error in terms of the number of samples, dimensions of the process, the lag $p$ and other key statistical properties of the model. The ideas presented can be used in the high-dimensional analysis of regularized $M$-estimators for other sparse nonlinear and non-Gaussian processes with long-range dependence.

Rigorous Dynamics and Consistent Estimation in Arbitrarily Conditioned Linear Systems

The problem of estimating a random vector x from noisy linear measurements y = A x + w with unknown parameters on the distributions of x and w, which must also be learned, arises in a wide range of statistical learning and linear inverse problems. We show that a computationally simple iterative message-passing algorithm can provably obtain asymptotically consistent estimates in a certain high-dimensional large-system limit (LSL) under very general parameterizations. Previous message passing techniques have required i.i.d. sub-Gaussian A matrices and often fail when the matrix is ill-conditioned. The proposed algorithm, called adaptive vector approximate message passing (Adaptive VAMP) with auto-tuning, applies to all right-rotationally random A. Importantly, this class includes matrices with arbitrarily poor conditioning. We show that the parameter estimates and mean squared error (MSE) of x in each iteration converge to deterministic limits that can be precisely predicted by a simple set of state evolution (SE) equations. In addition, a simple testable condition is provided in which the MSE matches the Bayes-optimal value predicted by the replica method. The paper thus provides a computationally simple method with provable guarantees of optimality and consistency over a large class of linear inverse problems.

Expectation Consistent Approximate Inference: Generalizations and Convergence

Approximations of loopy belief propagation, including expectation propagation and approximate message passing, have attracted considerable attention for probabilistic inference problems. This paper proposes and analyzes a generalization of Opper and Winther's expectation consistent (EC) approximate inference method. The proposed method, called Generalized Expectation Consistency (GEC), can be applied to both maximum a posteriori (MAP) and minimum mean squared error (MMSE) estimation. Here we characterize its fixed points, convergence, and performance relative to the replica prediction of optimality.