Low-Rank Nonlinear Decoding of $μ$-ECoG from the Primary Auditory Cortex
Paper and Code
May 06, 2020
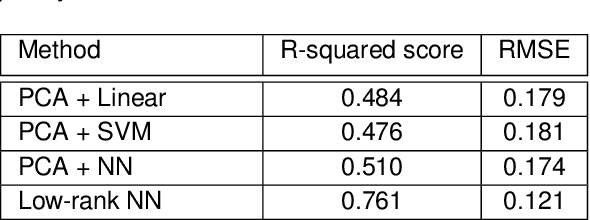

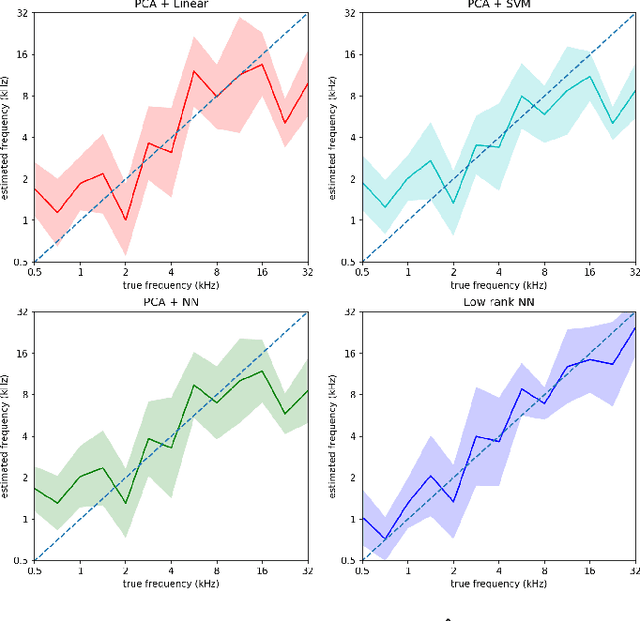
This paper considers the problem of neural decoding from parallel neural measurements systems such as micro-electrocorticography ($\mu$-ECoG). In systems with large numbers of array elements at very high sampling rates, the dimension of the raw measurement data may be large. Learning neural decoders for this high-dimensional data can be challenging, particularly when the number of training samples is limited. To address this challenge, this work presents a novel neural network decoder with a low-rank structure in the first hidden layer. The low-rank constraints dramatically reduce the number of parameters in the decoder while still enabling a rich class of nonlinear decoder maps. The low-rank decoder is illustrated on $\mu$-ECoG data from the primary auditory cortex (A1) of awake rats. This decoding problem is particularly challenging due to the complexity of neural responses in the auditory cortex and the presence of confounding signals in awake animals. It is shown that the proposed low-rank decoder significantly outperforms models using standard dimensionality reduction techniques such as principal component analysis (PCA).
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge