Philip Schniter
Conformal Bounds on Full-Reference Image Quality for Imaging Inverse Problems
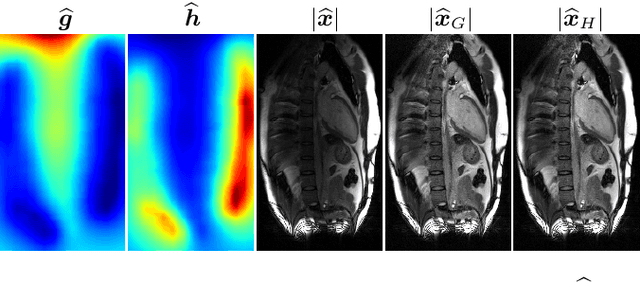
May 14, 2025Abstract:In imaging inverse problems, we would like to know how close the recovered image is to the true image in terms of full-reference image quality (FRIQ) metrics like PSNR, SSIM, LPIPS, etc. This is especially important in safety-critical applications like medical imaging, where knowing that, say, the SSIM was poor could potentially avoid a costly misdiagnosis. But since we don't know the true image, computing FRIQ is non-trivial. In this work, we combine conformal prediction with approximate posterior sampling to construct bounds on FRIQ that are guaranteed to hold up to a user-specified error probability. We demonstrate our approach on image denoising and accelerated magnetic resonance imaging (MRI) problems. Code is available at https://github.com/jwen307/quality_uq.
Solving Inverse Problems using Diffusion with Fast Iterative Renoising
Jan 29, 2025



Abstract:Imaging inverse problems can be solved in an unsupervised manner using pre-trained diffusion models. In most cases, that involves approximating the gradient of the measurement-conditional score function in the reverse process. Since the approximations produced by existing methods are quite poor, especially early in the reverse process, we propose a new approach that re-estimates and renoises the image several times per diffusion step. Renoising adds carefully shaped colored noise that ensures the pre-trained diffusion model sees white-Gaussian error, in accordance with how it was trained. We demonstrate the effectiveness of our "DDfire" method at 20, 100, and 1000 neural function evaluations on linear inverse problems and phase retrieval.
Score Combining for Contrastive OOD Detection
Jan 21, 2025Abstract:In out-of-distribution (OOD) detection, one is asked to classify whether a test sample comes from a known inlier distribution or not. We focus on the case where the inlier distribution is defined by a training dataset and there exists no additional knowledge about the novelties that one is likely to encounter. This problem is also referred to as novelty detection, one-class classification, and unsupervised anomaly detection. The current literature suggests that contrastive learning techniques are state-of-the-art for OOD detection. We aim to improve on those techniques by combining/ensembling their scores using the framework of null hypothesis testing and, in particular, a novel generalized likelihood ratio test (GLRT). We demonstrate that our proposed GLRT-based technique outperforms the state-of-the-art CSI and SupCSI techniques from Tack et al. 2020 in dataset-vs-dataset experiments with CIFAR-10, SVHN, LSUN, ImageNet, and CIFAR-100, as well as leave-one-class-out experiments with CIFAR-10. We also demonstrate that our GLRT outperforms the score-combining methods of Fisher, Bonferroni, Simes, Benjamini-Hochwald, and Stouffer in our application.
pcaGAN: Improving Posterior-Sampling cGANs via Principal Component Regularization
Nov 01, 2024Abstract:In ill-posed imaging inverse problems, there can exist many hypotheses that fit both the observed measurements and prior knowledge of the true image. Rather than returning just one hypothesis of that image, posterior samplers aim to explore the full solution space by generating many probable hypotheses, which can later be used to quantify uncertainty or construct recoveries that appropriately navigate the perception/distortion trade-off. In this work, we propose a fast and accurate posterior-sampling conditional generative adversarial network (cGAN) that, through a novel form of regularization, aims for correctness in the posterior mean as well as the trace and K principal components of the posterior covariance matrix. Numerical experiments demonstrate that our method outperforms contemporary cGANs and diffusion models in imaging inverse problems like denoising, large-scale inpainting, and accelerated MRI recovery. The code for our model can be found here: https://github.com/matt-bendel/pcaGAN.
Image Registration with Averaging Network and Edge-Based Loss for Low-SNR Cardiac MRI
Sep 04, 2024Abstract:Purpose: To perform image registration and averaging of multiple free-breathing single-shot cardiac images, where the individual images may have a low signal-to-noise ratio (SNR). Methods: To address low SNR encountered in single-shot imaging, especially at low field strengths, we propose a fast deep learning (DL)-based image registration method, called Averaging Morph with Edge Detection (AiM-ED). AiM-ED jointly registers multiple noisy source images to a noisy target image and utilizes a noise-robust pre-trained edge detector to define the training loss. We validate AiM-ED using synthetic late gadolinium enhanced (LGE) imaging data from the MR extended cardiac-torso (MRXCAT) phantom and retrospectively undersampled single-shot data from healthy subjects (24 slices) and patients (5 slices) under various levels of added noise. Additionally, we demonstrate the clinical feasibility of AiM-ED by applying it to prospectively undersampled data from patients (6 slices) scanned at a 0.55T scanner. Results: Compared to a traditional energy-minimization-based image registration method and DL-based VoxelMorph, images registered using AiM-ED exhibit higher values of recovery SNR and three perceptual image quality metrics. An ablation study shows the benefit of both jointly processing multiple source images and using an edge map in AiM-ED. Conclusion: For single-shot LGE imaging, AiM-ED outperforms existing image registration methods in terms of image quality. With fast inference, minimal training data requirements, and robust performance at various noise levels, AiM-ED has the potential to benefit single-shot CMR applications.
Fast and Robust Phase Retrieval via Deep Expectation-Consistent Approximation
Jul 12, 2024Abstract:Accurately recovering images from phaseless measurements is a challenging and long-standing problem. In this work, we present "deepECpr," which combines expectation-consistent (EC) approximation with deep denoising networks to surpass state-of-the-art phase-retrieval methods in both speed and accuracy. In addition to applying EC in a non-traditional manner, deepECpr includes a novel stochastic damping scheme that is inspired by recent diffusion methods. Like existing phase-retrieval methods based on plug-and-play priors, regularization by denoising, or diffusion, deepECpr iterates a denoising stage with a measurement-exploitation stage. But unlike existing methods, deepECpr requires far fewer denoiser calls. We compare deepECpr to the state-of-the-art prDeep (Metzler et al., 2018), Deep-ITA (Wang et al., 2020), and Diffusion Posterior Sampling (Chung et al., 2023) methods for noisy phase-retrieval of color, natural, and unnatural grayscale images on oversampled-Fourier and coded-diffraction-pattern measurements and find improvements in both PSNR and SSIM with 5x fewer denoiser calls.
Task-Driven Uncertainty Quantification in Inverse Problems via Conformal Prediction
May 28, 2024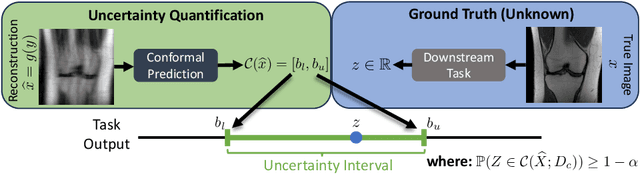

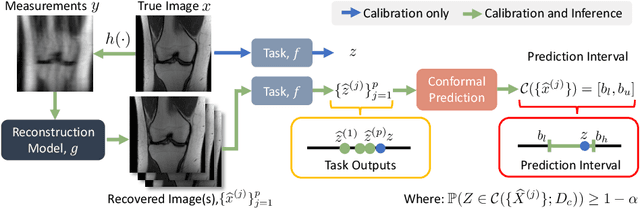

Abstract:In imaging inverse problems, one seeks to recover an image from missing/corrupted measurements. Because such problems are ill-posed, there is great motivation to quantify the uncertainty induced by the measurement-and-recovery process. Motivated by applications where the recovered image is used for a downstream task, such as soft-output classification, we propose a task-centered approach to uncertainty quantification. In particular, we use conformal prediction to construct an interval that is guaranteed to contain the task output from the true image up to a user-specified probability, and we use the width of that interval to quantify the uncertainty contributed by measurement-and-recovery. For posterior-sampling-based image recovery, we construct locally adaptive prediction intervals. Furthermore, we propose to collect measurements over multiple rounds, stopping as soon as the task uncertainty falls below an acceptable level. We demonstrate our methodology on accelerated magnetic resonance imaging (MRI).
Surface Coil Intensity Correction for MRI
Dec 01, 2023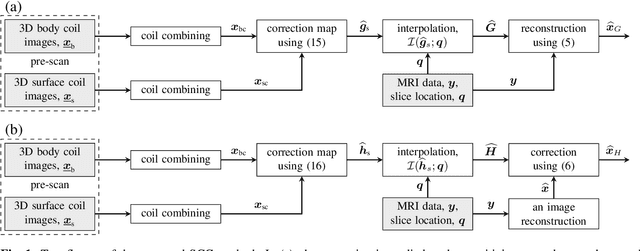
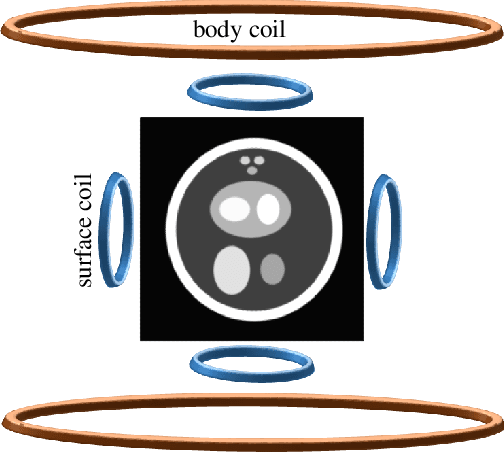
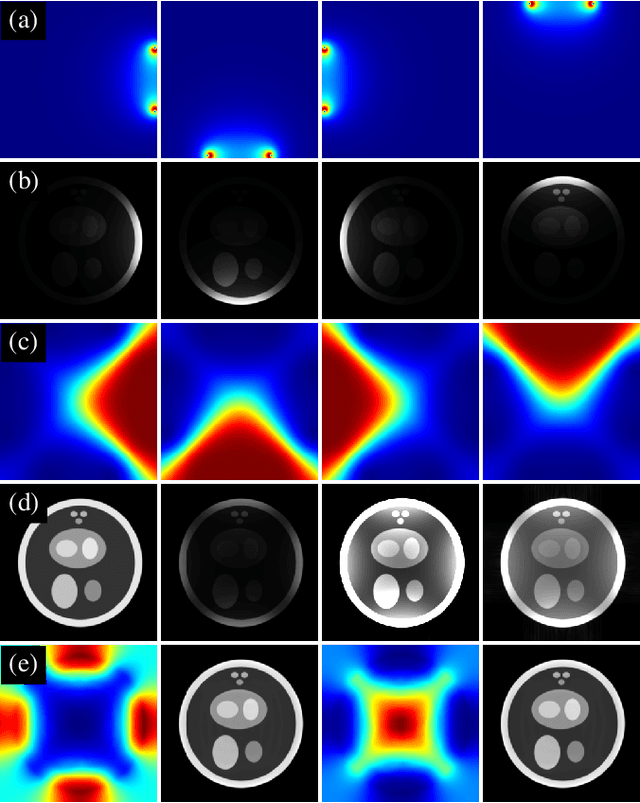
Abstract:Modern MRI scanners utilize one or more arrays of small receive-only coils to collect k-space data. The sensitivity maps of the coils, when estimated using traditional methods, differ from the true sensitivity maps, which are generally unknown. Consequently, the reconstructed MR images exhibit undesired spatial variation in intensity. These intensity variations can be at least partially corrected using pre-scan data. In this work, we propose an intensity correction method that utilizes pre-scan data. For demonstration, we apply our method to a digital phantom, as well as to cardiac MRI data collected from a commercial scanner by Siemens Healthineers. The code is available at https://github.com/OSU-MR/SCC.
A Conditional Normalizing Flow for Accelerated Multi-Coil MR Imaging
Jun 02, 2023Abstract:Accelerated magnetic resonance (MR) imaging attempts to reduce acquisition time by collecting data below the Nyquist rate. As an ill-posed inverse problem, many plausible solutions exist, yet the majority of deep learning approaches generate only a single solution. We instead focus on sampling from the posterior distribution, which provides more comprehensive information for downstream inference tasks. To do this, we design a novel conditional normalizing flow (CNF) that infers the signal component in the measurement operator's nullspace, which is later combined with measured data to form complete images. Using fastMRI brain and knee data, we demonstrate fast inference and accuracy that surpasses recent posterior sampling techniques for MRI. Code is available at https://github.com/jwen307/mri_cnf/
MRI Recovery with Self-Calibrated Denoisers without Fully-Sampled Data
Apr 25, 2023Abstract:PURPOSE: To present and validate a self-supervised MRI reconstruction method that does not require fully sampled k-space data. METHODS: ReSiDe is inspired by plug-and-play (PnP) methods and employs a denoiser as a regularizer. In contrast to traditional PnP approaches that utilize generic denoisers or train deep learning-based denoisers using high-quality images or image patches, ReSiDe directly trains the denoiser on the image or images being reconstructed from the undersampled data. We introduce two variations of our method, ReSiDe-S and ReSiDe-M. ReSiDe-S is scan-specific and works with a single set of undersampled measurements, while ReSiDe-M operates on multiple sets of undersampled measurements. More importantly, the trained denoisers in ReSiDe-M are stored for PnP recovery without further training. To improve robustness, the denoising strength in ReSiDe-S and ReSiDe- M is auto-tuned using the discrepancy principle. RESULTS: Studies I, II, and III compare ReSiDe-S and ReSiDe-M against other self-supervised or unsupervised methods using data from T1- and T2-weighted brain MRI, MRXCAT digital perfusion phantom, and first-pass cardiac perfusion, respectively. ReSiDe-S and ReSiDe-M outperform other methods in terms of reconstruction signal-to-noise ratio and structural similarity index measure for Studies I and II and in terms of expert scoring for Study III. CONCLUSION: A self-supervised image reconstruction method is presented and validated in both static and dynamic MRI applications. These developments can benefit MRI applications where availability of fully sampled training data is limited.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge