Solving Inverse Problems using Diffusion with Fast Iterative Renoising

Imaging inverse problems can be solved in an unsupervised manner using pre-trained diffusion models. In most cases, that involves approximating the gradient of the measurement-conditional score function in the reverse process. Since the approximations produced by existing methods are quite poor, especially early in the reverse process, we propose a new approach that re-estimates and renoises the image several times per diffusion step. Renoising adds carefully shaped colored noise that ensures the pre-trained diffusion model sees white-Gaussian error, in accordance with how it was trained. We demonstrate the effectiveness of our "DDfire" method at 20, 100, and 1000 neural function evaluations on linear inverse problems and phase retrieval.

Fast and Robust Phase Retrieval via Deep Expectation-Consistent Approximation

Accurately recovering images from phaseless measurements is a challenging and long-standing problem. In this work, we present "deepECpr," which combines expectation-consistent (EC) approximation with deep denoising networks to surpass state-of-the-art phase-retrieval methods in both speed and accuracy. In addition to applying EC in a non-traditional manner, deepECpr includes a novel stochastic damping scheme that is inspired by recent diffusion methods. Like existing phase-retrieval methods based on plug-and-play priors, regularization by denoising, or diffusion, deepECpr iterates a denoising stage with a measurement-exploitation stage. But unlike existing methods, deepECpr requires far fewer denoiser calls. We compare deepECpr to the state-of-the-art prDeep (Metzler et al., 2018), Deep-ITA (Wang et al., 2020), and Diffusion Posterior Sampling (Chung et al., 2023) methods for noisy phase-retrieval of color, natural, and unnatural grayscale images on oversampled-Fourier and coded-diffraction-pattern measurements and find improvements in both PSNR and SSIM with 5x fewer denoiser calls.

Denoising Generalized Expectation-Consistent Approximation for MRI Image Recovery

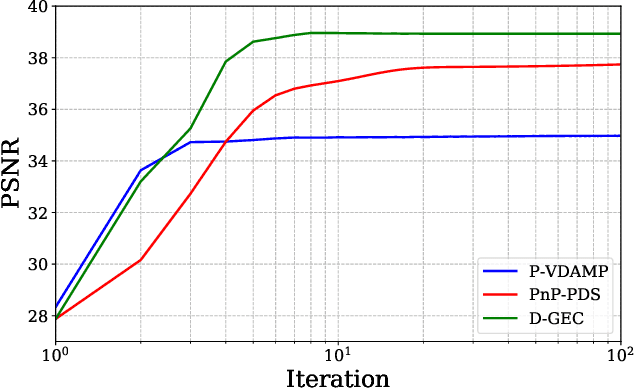
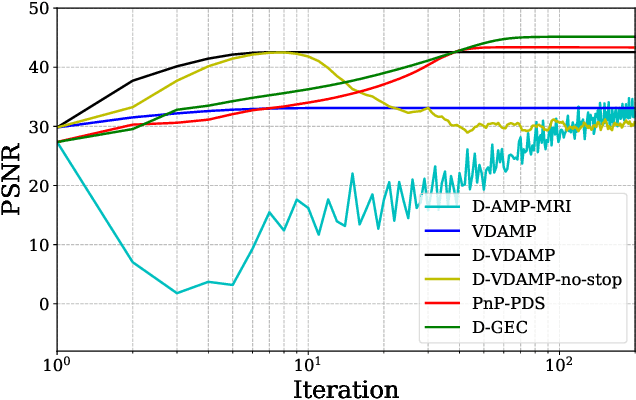
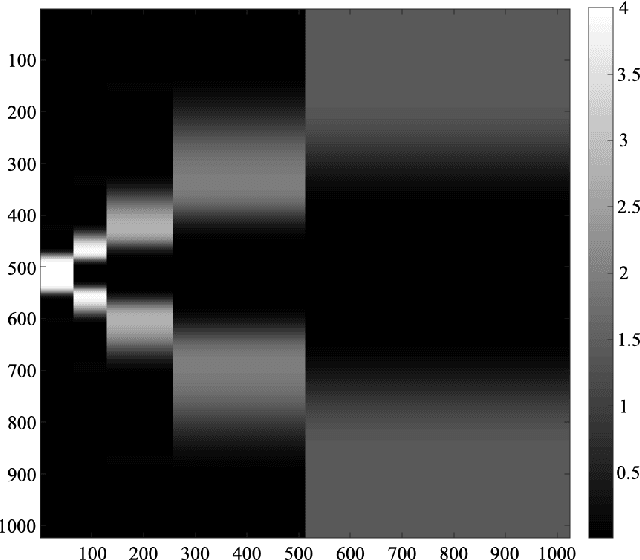
To solve inverse problems, plug-and-play (PnP) methods have been developed that replace the proximal step in a convex optimization algorithm with a call to an application-specific denoiser, often implemented using a deep neural network (DNN). Although such methods have been successful, they can be improved. For example, denoisers are usually designed/trained to remove white Gaussian noise, but the denoiser input error in PnP algorithms is usually far from white or Gaussian. Approximate message passing (AMP) methods provide white and Gaussian denoiser input error, but only when the forward operator is a large random matrix. In this work, for Fourier-based forward operators, we propose a PnP algorithm based on generalized expectation-consistent (GEC) approximation -- a close cousin of AMP -- that offers predictable error statistics at each iteration, as well as a new DNN denoiser that leverages those statistics. We apply our approach to magnetic resonance imaging (MRI) image recovery and demonstrate its advantages over existing PnP and AMP methods.