Denoising Generalized Expectation-Consistent Approximation for MRI Image Recovery
Paper and Code
Jun 09, 2022
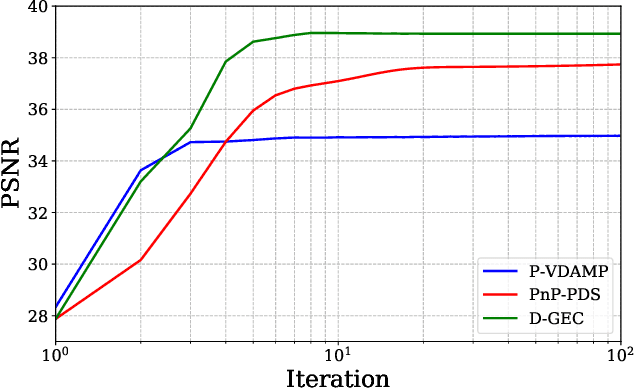
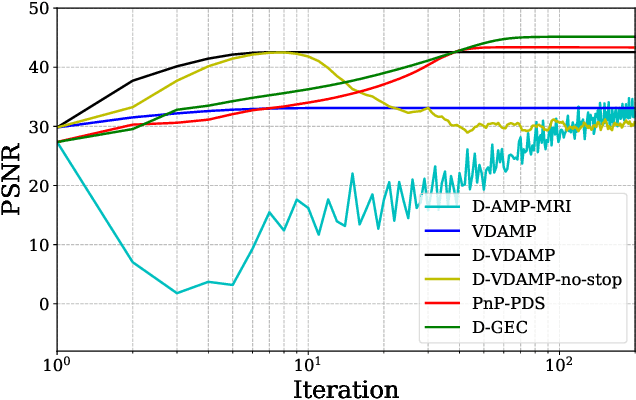
To solve inverse problems, plug-and-play (PnP) methods have been developed that replace the proximal step in a convex optimization algorithm with a call to an application-specific denoiser, often implemented using a deep neural network (DNN). Although such methods have been successful, they can be improved. For example, denoisers are usually designed/trained to remove white Gaussian noise, but the denoiser input error in PnP algorithms is usually far from white or Gaussian. Approximate message passing (AMP) methods provide white and Gaussian denoiser input error, but only when the forward operator is a large random matrix. In this work, for Fourier-based forward operators, we propose a PnP algorithm based on generalized expectation-consistent (GEC) approximation -- a close cousin of AMP -- that offers predictable error statistics at each iteration, as well as a new DNN denoiser that leverages those statistics. We apply our approach to magnetic resonance imaging (MRI) image recovery and demonstrate its advantages over existing PnP and AMP methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge