Task-Driven Uncertainty Quantification in Inverse Problems via Conformal Prediction
Paper and Code
May 28, 2024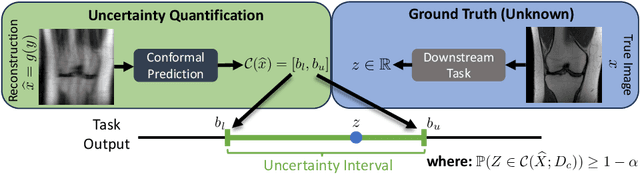

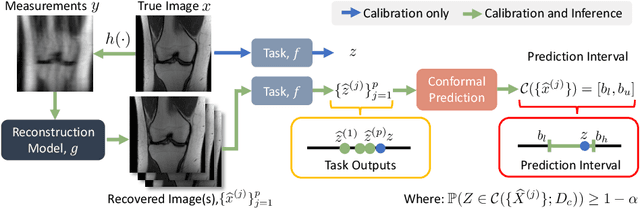

In imaging inverse problems, one seeks to recover an image from missing/corrupted measurements. Because such problems are ill-posed, there is great motivation to quantify the uncertainty induced by the measurement-and-recovery process. Motivated by applications where the recovered image is used for a downstream task, such as soft-output classification, we propose a task-centered approach to uncertainty quantification. In particular, we use conformal prediction to construct an interval that is guaranteed to contain the task output from the true image up to a user-specified probability, and we use the width of that interval to quantify the uncertainty contributed by measurement-and-recovery. For posterior-sampling-based image recovery, we construct locally adaptive prediction intervals. Furthermore, we propose to collect measurements over multiple rounds, stopping as soon as the task uncertainty falls below an acceptable level. We demonstrate our methodology on accelerated magnetic resonance imaging (MRI).
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge