An Interpretable Graph Generative Model with Heterophily

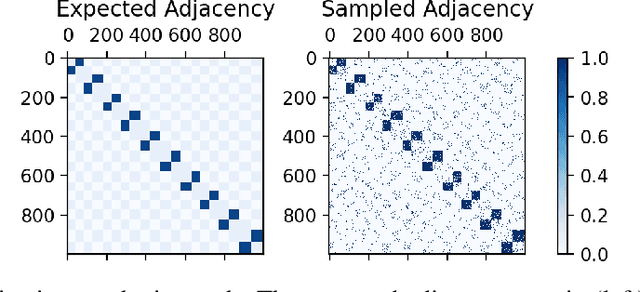
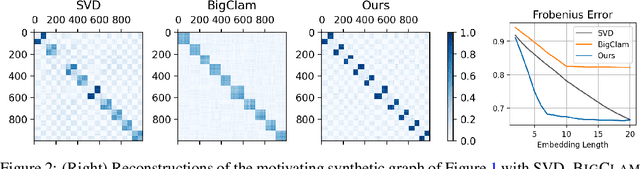
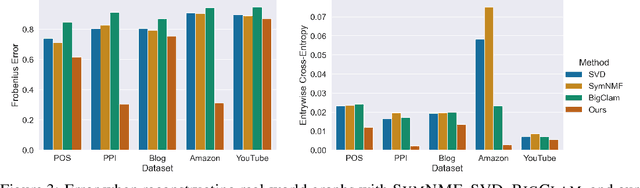
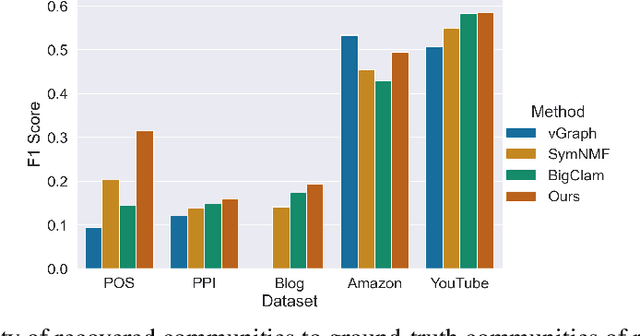
Many models for graphs fall under the framework of edge-independent dot product models. These models output the probabilities of edges existing between all pairs of nodes, and the probability of a link between two nodes increases with the dot product of vectors associated with the nodes. Recent work has shown that these models are unable to capture key structures in real-world graphs, particularly heterophilous structures, wherein links occur between dissimilar nodes. We propose the first edge-independent graph generative model that is a) expressive enough to capture heterophily, b) produces nonnegative embeddings, which allow link predictions to be interpreted in terms of communities, and c) optimizes effectively on real-world graphs with gradient descent on a cross-entropy loss. Our theoretical results demonstrate the expressiveness of our model in its ability to exactly reconstruct a graph using a number of clusters that is linear in the maximum degree, along with its ability to capture both heterophily and homophily in the data. Further, our experiments demonstrate the effectiveness of our model for a variety of important application tasks such as multi-label clustering and link prediction.