Off-Policy Evaluation in Markov Decision Processes under Weak Distributional Overlap

Doubly robust methods hold considerable promise for off-policy evaluation in Markov decision processes (MDPs) under sequential ignorability: They have been shown to converge as $1/\sqrt{T}$ with the horizon $T$, to be statistically efficient in large samples, and to allow for modular implementation where preliminary estimation tasks can be executed using standard reinforcement learning techniques. Existing results, however, make heavy use of a strong distributional overlap assumption whereby the stationary distributions of the target policy and the data-collection policy are within a bounded factor of each other -- and this assumption is typically only credible when the state space of the MDP is bounded. In this paper, we re-visit the task of off-policy evaluation in MDPs under a weaker notion of distributional overlap, and introduce a class of truncated doubly robust (TDR) estimators which we find to perform well in this setting. When the distribution ratio of the target and data-collection policies is square-integrable (but not necessarily bounded), our approach recovers the large-sample behavior previously established under strong distributional overlap. When this ratio is not square-integrable, TDR is still consistent but with a slower-than-$1/\sqrt{T}$; furthermore, this rate of convergence is minimax over a class of MDPs defined only using mixing conditions. We validate our approach numerically and find that, in our experiments, appropriate truncation plays a major role in enabling accurate off-policy evaluation when strong distributional overlap does not hold.

A Model-free Closeness-of-influence Test for Features in Supervised Learning

Understanding the effect of a feature vector $x \in \mathbb{R}^d$ on the response value (label) $y \in \mathbb{R}$ is the cornerstone of many statistical learning problems. Ideally, it is desired to understand how a set of collected features combine together and influence the response value, but this problem is notoriously difficult, due to the high-dimensionality of data and limited number of labeled data points, among many others. In this work, we take a new perspective on this problem, and we study the question of assessing the difference of influence that the two given features have on the response value. We first propose a notion of closeness for the influence of features, and show that our definition recovers the familiar notion of the magnitude of coefficients in the parametric model. We then propose a novel method to test for the closeness of influence in general model-free supervised learning problems. Our proposed test can be used with finite number of samples with control on type I error rate, no matter the ground truth conditional law $\mathcal{L}(Y |X)$. We analyze the power of our test for two general learning problems i) linear regression, and ii) binary classification under mixture of Gaussian models, and show that under the proper choice of score function, an internal component of our test, with sufficient number of samples will achieve full statistical power. We evaluate our findings through extensive numerical simulations, specifically we adopt the datamodel framework (Ilyas, et al., 2022) for CIFAR-10 dataset to identify pairs of training samples with different influence on the trained model via optional black box training mechanisms.

GRASP: A Goodness-of-Fit Test for Classification Learning

Performance of classifiers is often measured in terms of average accuracy on test data. Despite being a standard measure, average accuracy fails in characterizing the fit of the model to the underlying conditional law of labels given the features vector ($Y|X$), e.g. due to model misspecification, over fitting, and high-dimensionality. In this paper, we consider the fundamental problem of assessing the goodness-of-fit for a general binary classifier. Our framework does not make any parametric assumption on the conditional law $Y|X$, and treats that as a black box oracle model which can be accessed only through queries. We formulate the goodness-of-fit assessment problem as a tolerance hypothesis testing of the form \[ H_0: \mathbb{E}\Big[D_f\Big({\sf Bern}(\eta(X))\|{\sf Bern}(\hat{\eta}(X))\Big)\Big]\leq \tau\,, \] where $D_f$ represents an $f$-divergence function, and $\eta(x)$, $\hat{\eta}(x)$ respectively denote the true and an estimate likelihood for a feature vector $x$ admitting a positive label. We propose a novel test, called \grasp for testing $H_0$, which works in finite sample settings, no matter the features (distribution-free). We also propose model-X \grasp designed for model-X settings where the joint distribution of the features vector is known. Model-X \grasp uses this distributional information to achieve better power. We evaluate the performance of our tests through extensive numerical experiments.

Adversarial robustness for latent models: Revisiting the robust-standard accuracies tradeoff

Over the past few years, several adversarial training methods have been proposed to improve the robustness of machine learning models against adversarial perturbations in the input. Despite remarkable progress in this regard, adversarial training is often observed to drop the standard test accuracy. This phenomenon has intrigued the research community to investigate the potential tradeoff between standard and robust accuracy as two performance measures. In this paper, we revisit this tradeoff for latent models and argue that this tradeoff is mitigated when the data enjoys a low-dimensional structure. In particular, we consider binary classification under two data generative models, namely Gaussian mixture model and generalized linear model, where the feature data lie on a low-dimensional manifold. We show that as the manifold dimension to the ambient dimension decreases, one can obtain models that are nearly optimal with respect to both, the standard accuracy and the robust accuracy measures.

Error-Correction for Sparse Support Recovery Algorithms

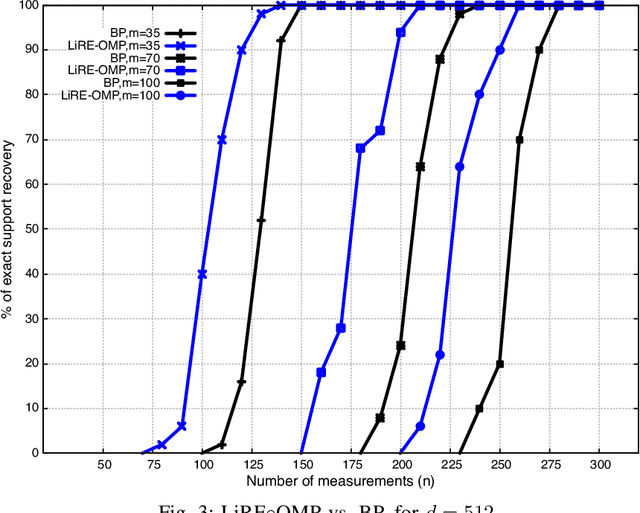
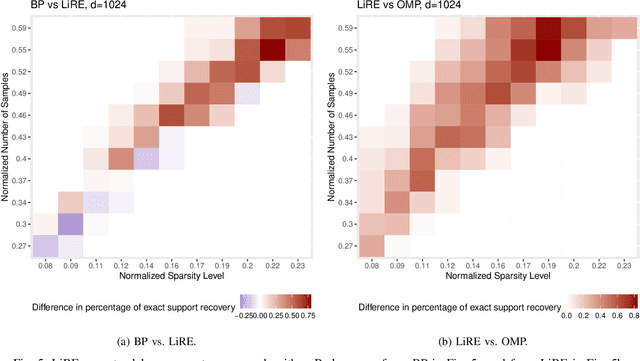
Consider the compressed sensing setup where the support $s^*$ of an $m$-sparse $d$-dimensional signal $x$ is to be recovered from $n$ linear measurements with a given algorithm. Suppose that the measurements are such that the algorithm does not guarantee perfect support recovery and that true features may be missed. Can they efficiently be retrieved? This paper addresses this question through a simple error-correction module referred to as LiRE. LiRE takes as input an estimate $s_{in}$ of the true support $s^*$, and outputs a refined support estimate $s_{out}$. In the noiseless measurement setup, sufficient conditions are established under which LiRE is guaranteed to recover the entire support, that is $s_{out}$ contains $s^*$. These conditions imply, for instance, that in the high-dimensional regime LiRE can correct a sublinear in $m$ number of errors made by Orthogonal Matching Pursuit (OMP). The computational complexity of LiRE is $O(mnd)$. Experimental results with random Gaussian design matrices show that LiRE substantially reduces the number of measurements needed for perfect support recovery via Compressive Sampling Matching Pursuit, Basis Pursuit (BP), and OMP. Interestingly, adding LiRE to OMP yields a support recovery procedure that is more accurate and significantly faster than BP. This observation carries over in the noisy measurement setup. Finally, as a standalone support recovery algorithm with a random initialization, experiments show that LiRE's reconstruction performance lies between OMP and BP. These results suggest that LiRE may be used generically, on top of any suboptimal baseline support recovery algorithm, to improve support recovery or to operate with a smaller number of measurements, at the cost of a relatively small computational overhead. Alternatively, LiRE may be used as a standalone support recovery algorithm that is competitive with respect to OMP.

Fundamental Tradeoffs in Distributionally Adversarial Training

Adversarial training is among the most effective techniques to improve the robustness of models against adversarial perturbations. However, the full effect of this approach on models is not well understood. For example, while adversarial training can reduce the adversarial risk (prediction error against an adversary), it sometimes increase standard risk (generalization error when there is no adversary). Even more, such behavior is impacted by various elements of the learning problem, including the size and quality of training data, specific forms of adversarial perturbations in the input, model overparameterization, and adversary's power, among others. In this paper, we focus on \emph{distribution perturbing} adversary framework wherein the adversary can change the test distribution within a neighborhood of the training data distribution. The neighborhood is defined via Wasserstein distance between distributions and the radius of the neighborhood is a measure of adversary's manipulative power. We study the tradeoff between standard risk and adversarial risk and derive the Pareto-optimal tradeoff, achievable over specific classes of models, in the infinite data limit with features dimension kept fixed. We consider three learning settings: 1) Regression with the class of linear models; 2) Binary classification under the Gaussian mixtures data model, with the class of linear classifiers; 3) Regression with the class of random features model (which can be equivalently represented as two-layer neural network with random first-layer weights). We show that a tradeoff between standard and adversarial risk is manifested in all three settings. We further characterize the Pareto-optimal tradeoff curves and discuss how a variety of factors, such as features correlation, adversary's power or the width of two-layer neural network would affect this tradeoff.

Online Debiasing for Adaptively Collected High-dimensional Data

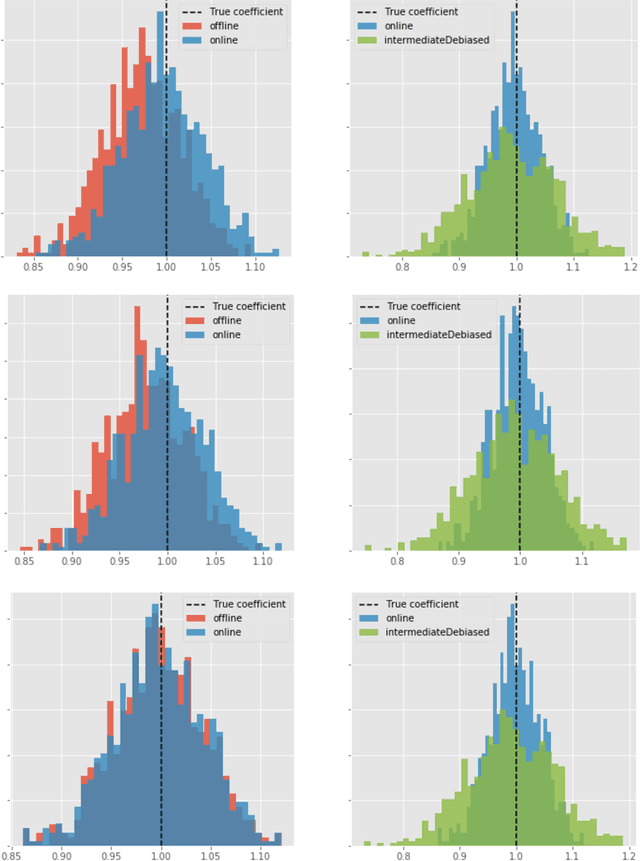
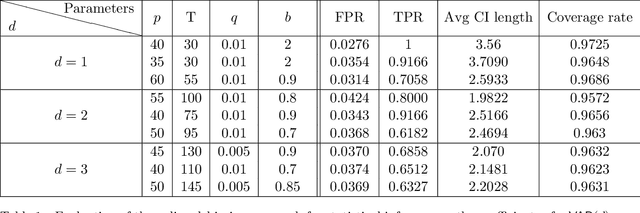
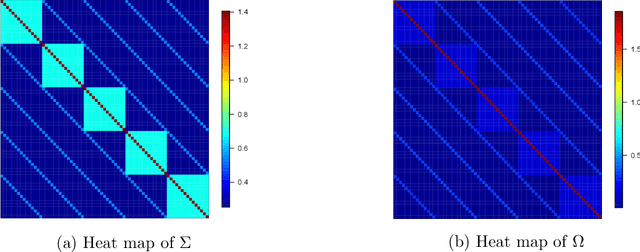
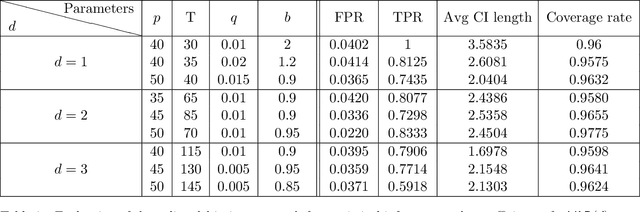
Adaptive collection of data is commonplace in applications throughout science and engineering. From the point of view of statistical inference however, adaptive data collection induces memory and correlation in the sample, and poses significant challenge. We consider the high-dimensional linear regression, where the sample is collected adaptively, and the sample size $n$ can be smaller than $p$, the number of covariates. In this setting, there are two distinct sources of bias: the first due to regularization imposed for consistent estimation, e.g. using the LASSO, and the second due to adaptivity in collecting the sample. We propose \emph{`online debiasing'}, a general procedure for estimators such as the LASSO, which addresses both sources of bias. In two concrete contexts $(i)$ batched data collection and $(ii)$ time series analysis, we demonstrate that online debiasing optimally debiases the LASSO estimate when the underlying parameter $\theta_0$ has sparsity of order $o(\sqrt{n}/\log p)$. In this regime, the debiased estimator can be used to compute $p$-values and confidence intervals of optimal size.

Bounds on the Approximation Power of Feedforward Neural Networks

The approximation power of general feedforward neural networks with piecewise linear activation functions is investigated. First, lower bounds on the size of a network are established in terms of the approximation error and network depth and width. These bounds improve upon state-of-the-art bounds for certain classes of functions, such as strongly convex functions. Second, an upper bound is established on the difference of two neural networks with identical weights but different activation functions.