Error-Correction for Sparse Support Recovery Algorithms
Paper and Code
Mar 05, 2021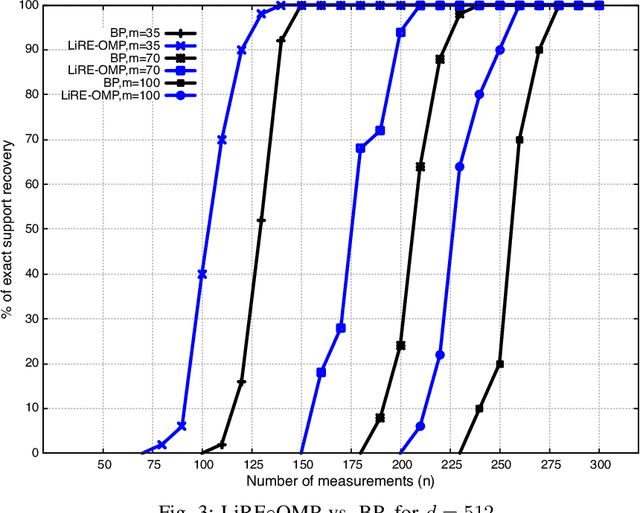
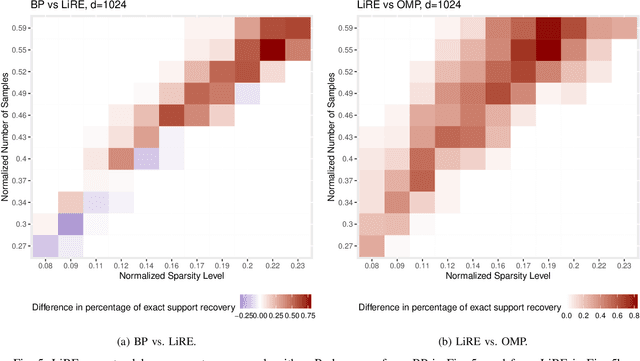
Consider the compressed sensing setup where the support $s^*$ of an $m$-sparse $d$-dimensional signal $x$ is to be recovered from $n$ linear measurements with a given algorithm. Suppose that the measurements are such that the algorithm does not guarantee perfect support recovery and that true features may be missed. Can they efficiently be retrieved? This paper addresses this question through a simple error-correction module referred to as LiRE. LiRE takes as input an estimate $s_{in}$ of the true support $s^*$, and outputs a refined support estimate $s_{out}$. In the noiseless measurement setup, sufficient conditions are established under which LiRE is guaranteed to recover the entire support, that is $s_{out}$ contains $s^*$. These conditions imply, for instance, that in the high-dimensional regime LiRE can correct a sublinear in $m$ number of errors made by Orthogonal Matching Pursuit (OMP). The computational complexity of LiRE is $O(mnd)$. Experimental results with random Gaussian design matrices show that LiRE substantially reduces the number of measurements needed for perfect support recovery via Compressive Sampling Matching Pursuit, Basis Pursuit (BP), and OMP. Interestingly, adding LiRE to OMP yields a support recovery procedure that is more accurate and significantly faster than BP. This observation carries over in the noisy measurement setup. Finally, as a standalone support recovery algorithm with a random initialization, experiments show that LiRE's reconstruction performance lies between OMP and BP. These results suggest that LiRE may be used generically, on top of any suboptimal baseline support recovery algorithm, to improve support recovery or to operate with a smaller number of measurements, at the cost of a relatively small computational overhead. Alternatively, LiRE may be used as a standalone support recovery algorithm that is competitive with respect to OMP.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge