OpenAirLink: Reproducible Wireless Channel Emulation using Software Defined Radios

This paper presents OpenAirLink(OAL), an open-source channel emulator for reproducible testing of wireless scenarios. OAL is implemented on off-the-shelf software-defined radios (SDR) and presents a smaller-scale alternative to expensive commercially available channel emulators. Path loss and propagation delay are the fundamental aspects of emulating a wireless channel. OAL provides a simple method to change these aspects in real-time. The emulator is implemented using a finite impulse response (FIR) filter. The FIR filter is written in Verilog and flashed on the SDRs Field Programmable Gate Array (FPGA). Most processing transpires on the FPGA, so OAL does not require high-performance computing hardware and SDRs. We validate the performance of OAL and demonstrate the utility of such a channel emulation tool using two examples. We believe that open-source channel emulators such as OAL can make reproducible wireless experiments accessible to many researchers in the scientific community.

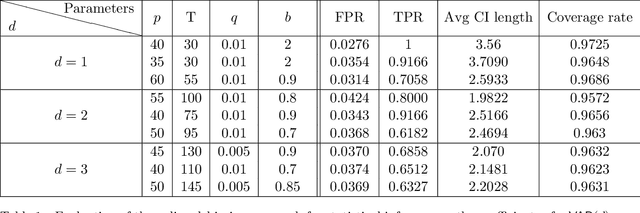
Near-optimal inference in adaptive linear regression

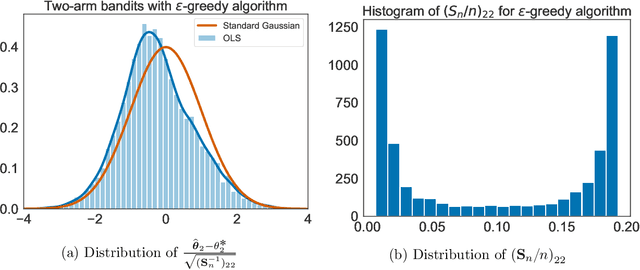
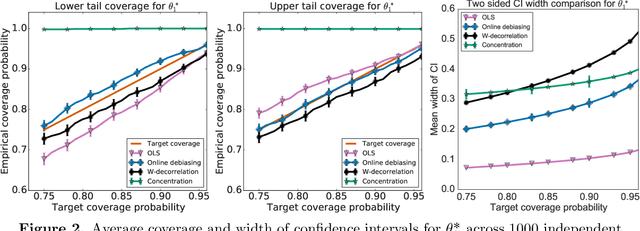
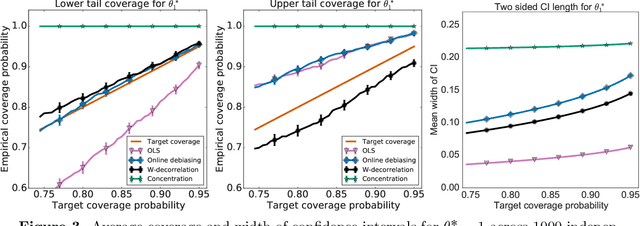
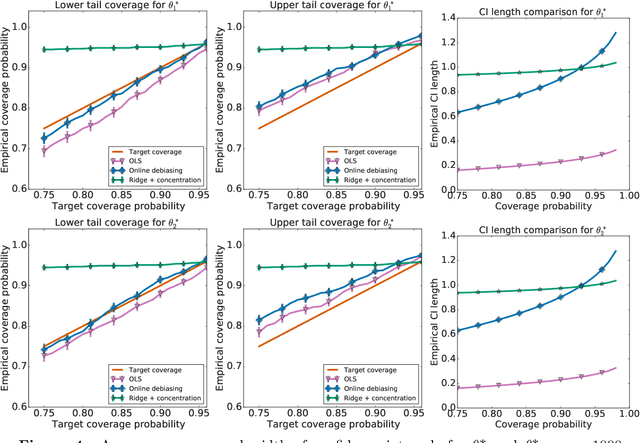
When data is collected in an adaptive manner, even simple methods like ordinary least squares can exhibit non-normal asymptotic behavior. As an undesirable consequence, hypothesis tests and confidence intervals based on asymptotic normality can lead to erroneous results. We propose an online debiasing estimator to correct these distributional anomalies in least squares estimation. Our proposed method takes advantage of the covariance structure present in the dataset and provides sharper estimates in directions for which more information has accrued. We establish an asymptotic normality property for our proposed online debiasing estimator under mild conditions on the data collection process, and provide asymptotically exact confidence intervals. We additionally prove a minimax lower bound for the adaptive linear regression problem, thereby providing a baseline by which to compare estimators. There are various conditions under which our proposed estimator achieves the minimax lower bound up to logarithmic factors. We demonstrate the usefulness of our theory via applications to multi-armed bandit, autoregressive time series estimation, and active learning with exploration.

VisualSem: a high-quality knowledge graph for vision and language

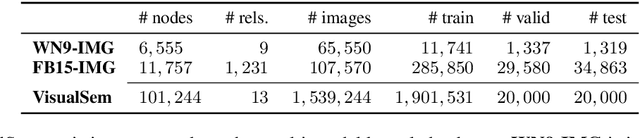
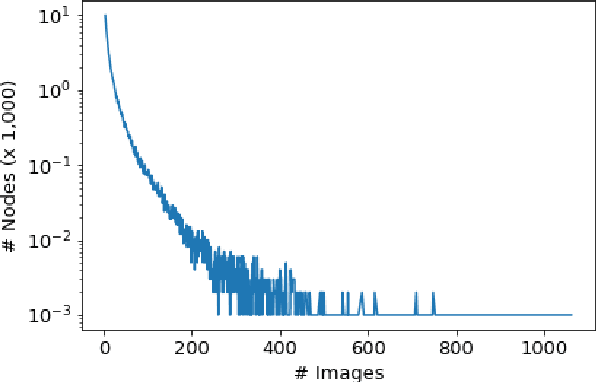
We argue that the next frontier in natural language understanding (NLU) and generation (NLG) will include models that can efficiently access external structured knowledge repositories. In order to support the development of such models, we release the VisualSem knowledge graph (KG) which includes nodes with multilingual glosses and multiple illustrative images and visually relevant relations. We also release a neural multi-modal retrieval model that can use images or sentences as inputs and retrieves entities in the KG. This multi-modal retrieval model can be integrated into any (neural network) model pipeline and we encourage the research community to use VisualSem for data augmentation and/or as a source of grounding, among other possible uses. VisualSem as well as the multi-modal retrieval model are publicly available and can be downloaded in: https://github.com/iacercalixto/visualsem.

Online Debiasing for Adaptively Collected High-dimensional Data

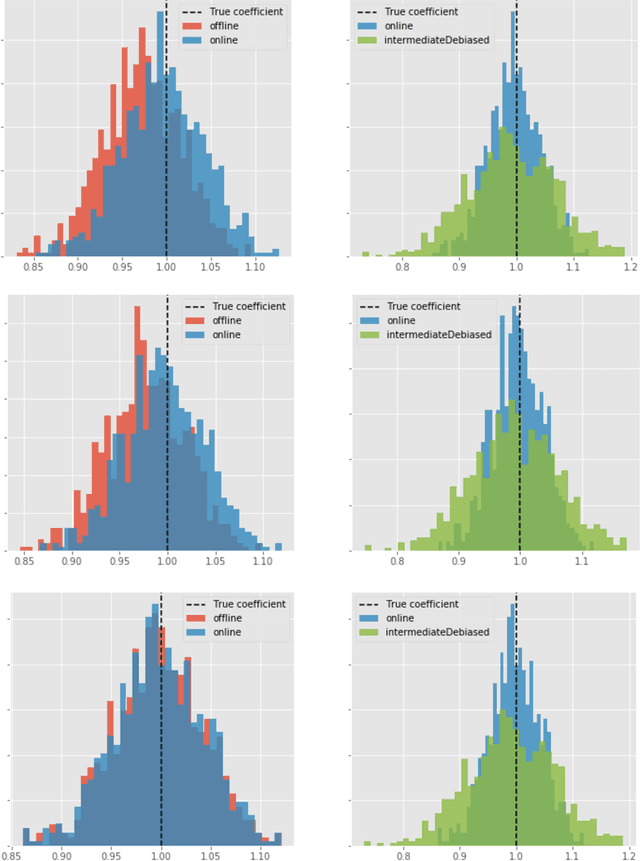
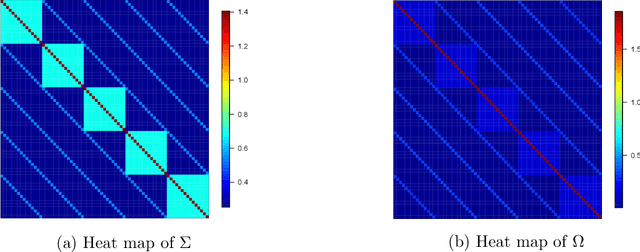
Adaptive collection of data is commonplace in applications throughout science and engineering. From the point of view of statistical inference however, adaptive data collection induces memory and correlation in the sample, and poses significant challenge. We consider the high-dimensional linear regression, where the sample is collected adaptively, and the sample size $n$ can be smaller than $p$, the number of covariates. In this setting, there are two distinct sources of bias: the first due to regularization imposed for consistent estimation, e.g. using the LASSO, and the second due to adaptivity in collecting the sample. We propose \emph{`online debiasing'}, a general procedure for estimators such as the LASSO, which addresses both sources of bias. In two concrete contexts $(i)$ batched data collection and $(ii)$ time series analysis, we demonstrate that online debiasing optimally debiases the LASSO estimate when the underlying parameter $\theta_0$ has sparsity of order $o(\sqrt{n}/\log p)$. In this regime, the debiased estimator can be used to compute $p$-values and confidence intervals of optimal size.

Contextual Stochastic Block Models

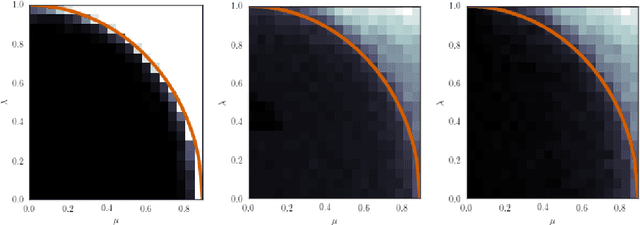
We provide the first information theoretic tight analysis for inference of latent community structure given a sparse graph along with high dimensional node covariates, correlated with the same latent communities. Our work bridges recent theoretical breakthroughs in the detection of latent community structure without nodes covariates and a large body of empirical work using diverse heuristics for combining node covariates with graphs for inference. The tightness of our analysis implies in particular, the information theoretical necessity of combining the different sources of information. Our analysis holds for networks of large degrees as well as for a Gaussian version of the model.

Accurate Inference for Adaptive Linear Models

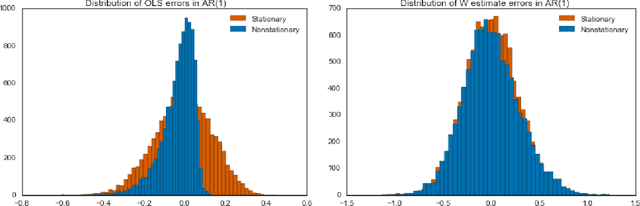
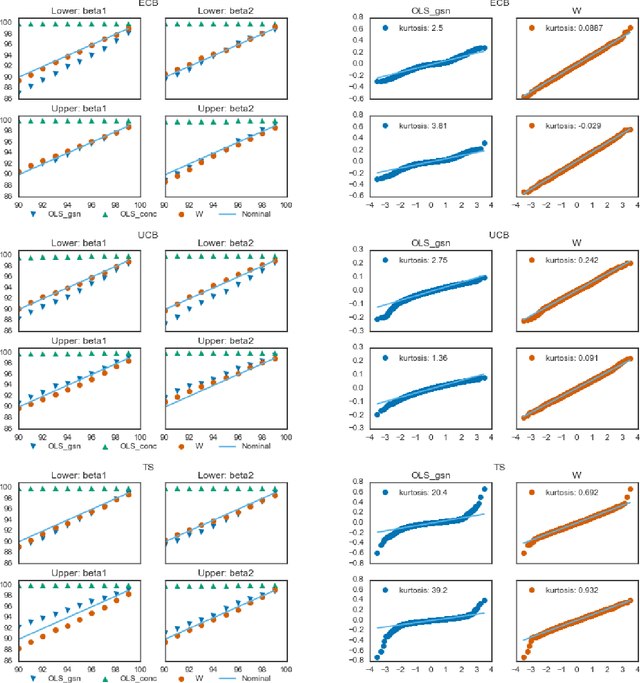
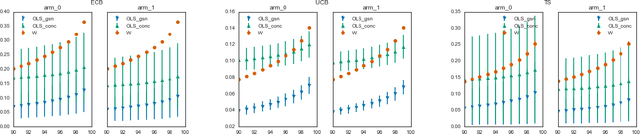
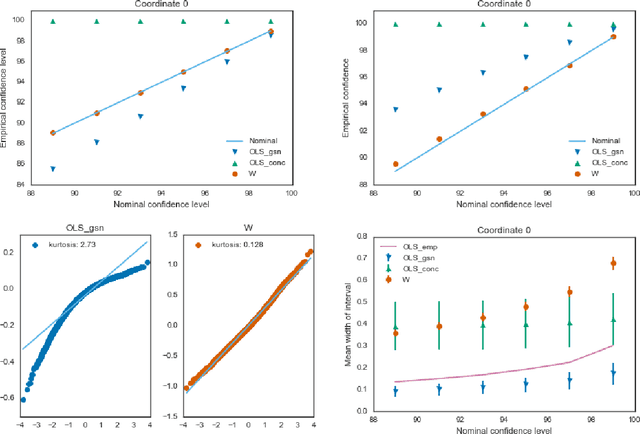
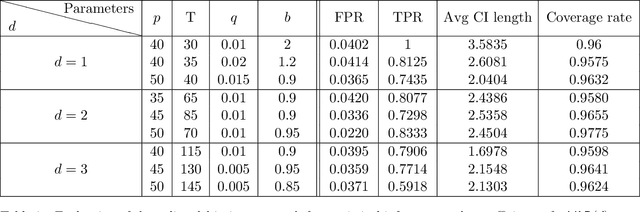
Estimators computed from adaptively collected data do not behave like their non-adaptive brethren. Rather, the sequential dependence of the collection policy can lead to severe distributional biases that persist even in the infinite data limit. We develop a general method -- $\mathbf{W}$-decorrelation -- for transforming the bias of adaptive linear regression estimators into variance. The method uses only coarse-grained information about the data collection policy and does not need access to propensity scores or exact knowledge of the policy. We bound the finite-sample bias and variance of the $\mathbf{W}$-estimator and develop asymptotically correct confidence intervals based on a novel martingale central limit theorem. We then demonstrate the empirical benefits of the generic $\mathbf{W}$-decorrelation procedure in two different adaptive data settings: the multi-armed bandit and the autoregressive time series.

Inference in Graphical Models via Semidefinite Programming Hierarchies

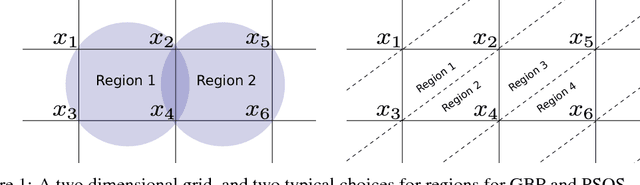
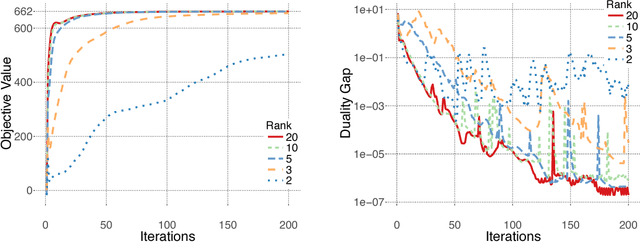
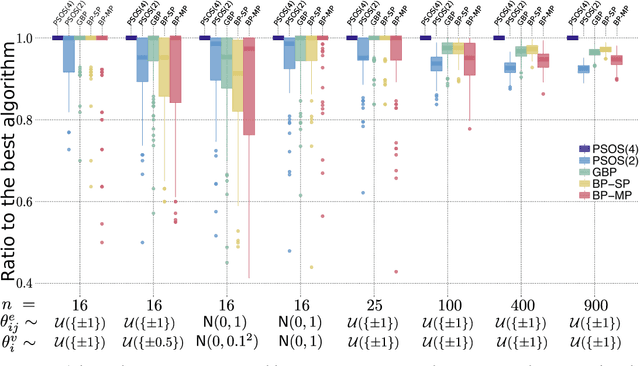
Maximum A posteriori Probability (MAP) inference in graphical models amounts to solving a graph-structured combinatorial optimization problem. Popular inference algorithms such as belief propagation (BP) and generalized belief propagation (GBP) are intimately related to linear programming (LP) relaxation within the Sherali-Adams hierarchy. Despite the popularity of these algorithms, it is well understood that the Sum-of-Squares (SOS) hierarchy based on semidefinite programming (SDP) can provide superior guarantees. Unfortunately, SOS relaxations for a graph with $n$ vertices require solving an SDP with $n^{\Theta(d)}$ variables where $d$ is the degree in the hierarchy. In practice, for $d\ge 4$, this approach does not scale beyond a few tens of variables. In this paper, we propose binary SDP relaxations for MAP inference using the SOS hierarchy with two innovations focused on computational efficiency. Firstly, in analogy to BP and its variants, we only introduce decision variables corresponding to contiguous regions in the graphical model. Secondly, we solve the resulting SDP using a non-convex Burer-Monteiro style method, and develop a sequential rounding procedure. We demonstrate that the resulting algorithm can solve problems with tens of thousands of variables within minutes, and outperforms BP and GBP on practical problems such as image denoising and Ising spin glasses. Finally, for specific graph types, we establish a sufficient condition for the tightness of the proposed partial SOS relaxation.

Sparse PCA via Covariance Thresholding

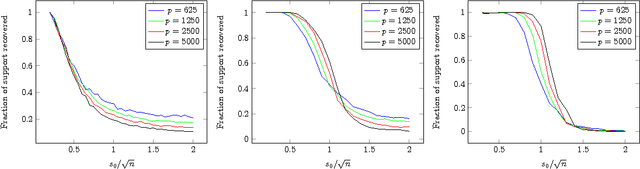
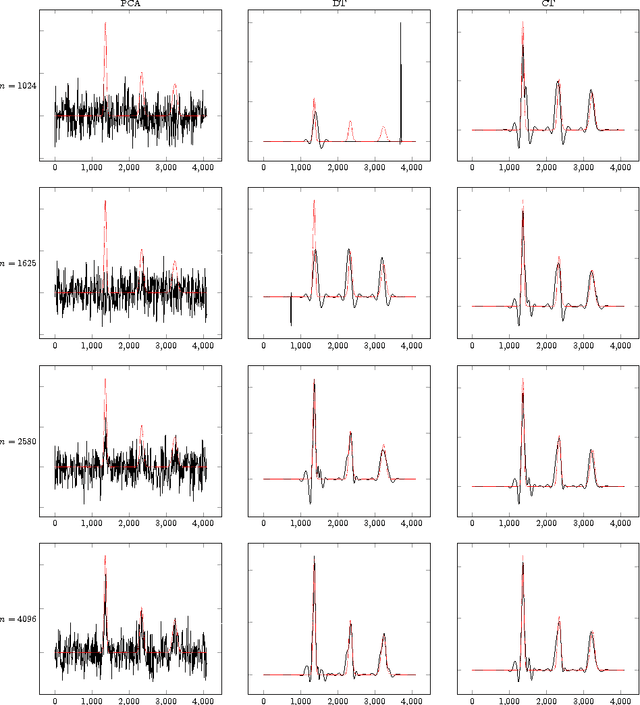
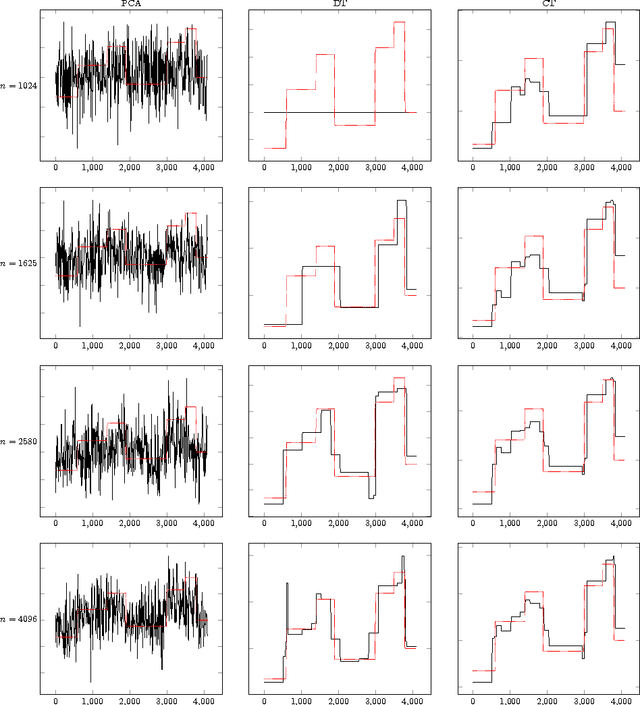
In sparse principal component analysis we are given noisy observations of a low-rank matrix of dimension $n\times p$ and seek to reconstruct it under additional sparsity assumptions. In particular, we assume here each of the principal components $\mathbf{v}_1,\dots,\mathbf{v}_r$ has at most $s_0$ non-zero entries. We are particularly interested in the high dimensional regime wherein $p$ is comparable to, or even much larger than $n$. In an influential paper, \cite{johnstone2004sparse} introduced a simple algorithm that estimates the support of the principal vectors $\mathbf{v}_1,\dots,\mathbf{v}_r$ by the largest entries in the diagonal of the empirical covariance. This method can be shown to identify the correct support with high probability if $s_0\le K_1\sqrt{n/\log p}$, and to fail with high probability if $s_0\ge K_2 \sqrt{n/\log p}$ for two constants $0<K_1,K_2<\infty$. Despite a considerable amount of work over the last ten years, no practical algorithm exists with provably better support recovery guarantees. Here we analyze a covariance thresholding algorithm that was recently proposed by \cite{KrauthgamerSPCA}. On the basis of numerical simulations (for the rank-one case), these authors conjectured that covariance thresholding correctly recover the support with high probability for $s_0\le K\sqrt{n}$ (assuming $n$ of the same order as $p$). We prove this conjecture, and in fact establish a more general guarantee including higher-rank as well as $n$ much smaller than $p$. Recent lower bounds \cite{berthet2013computational, ma2015sum} suggest that no polynomial time algorithm can do significantly better. The key technical component of our analysis develops new bounds on the norm of kernel random matrices, in regimes that were not considered before.

Improved Sum-of-Squares Lower Bounds for Hidden Clique and Hidden Submatrix Problems

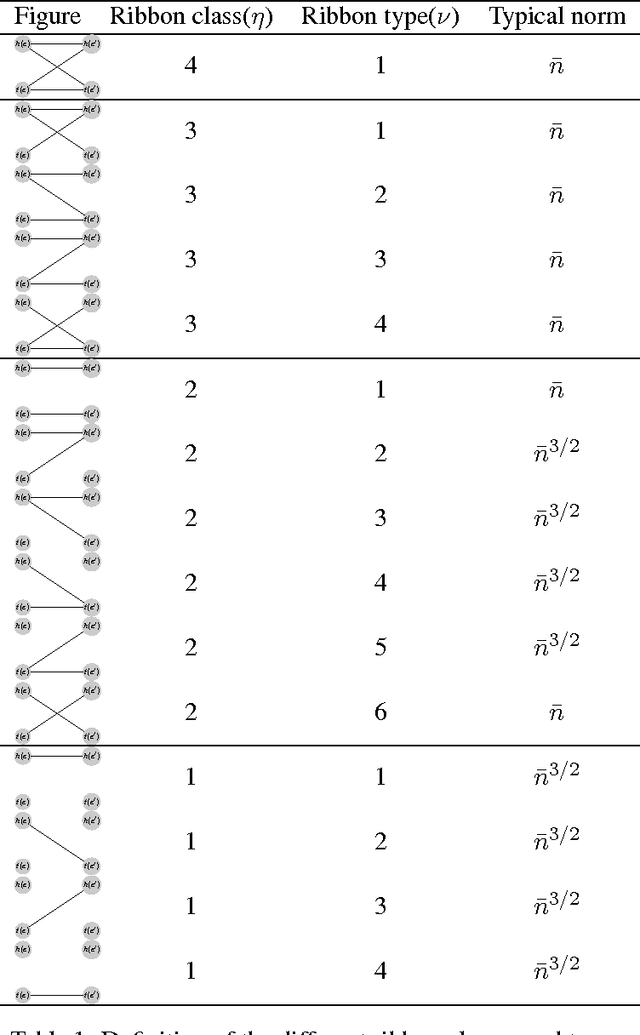
Given a large data matrix $A\in\mathbb{R}^{n\times n}$, we consider the problem of determining whether its entries are i.i.d. with some known marginal distribution $A_{ij}\sim P_0$, or instead $A$ contains a principal submatrix $A_{{\sf Q},{\sf Q}}$ whose entries have marginal distribution $A_{ij}\sim P_1\neq P_0$. As a special case, the hidden (or planted) clique problem requires to find a planted clique in an otherwise uniformly random graph. Assuming unbounded computational resources, this hypothesis testing problem is statistically solvable provided $|{\sf Q}|\ge C \log n$ for a suitable constant $C$. However, despite substantial effort, no polynomial time algorithm is known that succeeds with high probability when $|{\sf Q}| = o(\sqrt{n})$. Recently Meka and Wigderson \cite{meka2013association}, proposed a method to establish lower bounds within the Sum of Squares (SOS) semidefinite hierarchy. Here we consider the degree-$4$ SOS relaxation, and study the construction of \cite{meka2013association} to prove that SOS fails unless $k\ge C\, n^{1/3}/\log n$. An argument presented by Barak implies that this lower bound cannot be substantially improved unless the witness construction is changed in the proof. Our proof uses the moments method to bound the spectrum of a certain random association scheme, i.e. a symmetric random matrix whose rows and columns are indexed by the edges of an Erd\"os-Renyi random graph.

Linear Bandits in High Dimension and Recommendation Systems

A large number of online services provide automated recommendations to help users to navigate through a large collection of items. New items (products, videos, songs, advertisements) are suggested on the basis of the user's past history and --when available-- her demographic profile. Recommendations have to satisfy the dual goal of helping the user to explore the space of available items, while allowing the system to probe the user's preferences. We model this trade-off using linearly parametrized multi-armed bandits, propose a policy and prove upper and lower bounds on the cumulative "reward" that coincide up to constants in the data poor (high-dimensional) regime. Prior work on linear bandits has focused on the data rich (low-dimensional) regime and used cumulative "risk" as the figure of merit. For this data rich regime, we provide a simple modification for our policy that achieves near-optimal risk performance under more restrictive assumptions on the geometry of the problem. We test (a variation of) the scheme used for establishing achievability on the Netflix and MovieLens datasets and obtain good agreement with the qualitative predictions of the theory we develop.