Public-data Assisted Private Stochastic Optimization: Power and Limitations

We study the limits and capability of public-data assisted differentially private (PA-DP) algorithms. Specifically, we focus on the problem of stochastic convex optimization (SCO) with either labeled or unlabeled public data. For complete/labeled public data, we show that any $(\epsilon,\delta)$-PA-DP has excess risk $\tilde{\Omega}\big(\min\big\{\frac{1}{\sqrt{n_{\text{pub}}}},\frac{1}{\sqrt{n}}+\frac{\sqrt{d}}{n\epsilon} \big\} \big)$, where $d$ is the dimension, ${n_{\text{pub}}}$ is the number of public samples, ${n_{\text{priv}}}$ is the number of private samples, and $n={n_{\text{pub}}}+{n_{\text{priv}}}$. These lower bounds are established via our new lower bounds for PA-DP mean estimation, which are of a similar form. Up to constant factors, these lower bounds show that the simple strategy of either treating all data as private or discarding the private data, is optimal. We also study PA-DP supervised learning with \textit{unlabeled} public samples. In contrast to our previous result, we here show novel methods for leveraging public data in private supervised learning. For generalized linear models (GLM) with unlabeled public data, we show an efficient algorithm which, given $\tilde{O}({n_{\text{priv}}}\epsilon)$ unlabeled public samples, achieves the dimension independent rate $\tilde{O}\big(\frac{1}{\sqrt{{n_{\text{priv}}}}} + \frac{1}{\sqrt{{n_{\text{priv}}}\epsilon}}\big)$. We develop new lower bounds for this setting which shows that this rate cannot be improved with more public samples, and any fewer public samples leads to a worse rate. Finally, we provide extensions of this result to general hypothesis classes with finite fat-shattering dimension with applications to neural networks and non-Euclidean geometries.

Differentially Private Non-Convex Optimization under the KL Condition with Optimal Rates

We study private empirical risk minimization (ERM) problem for losses satisfying the $(\gamma,\kappa)$-Kurdyka-{\L}ojasiewicz (KL) condition. The Polyak-{\L}ojasiewicz (PL) condition is a special case of this condition when $\kappa=2$. Specifically, we study this problem under the constraint of $\rho$ zero-concentrated differential privacy (zCDP). When $\kappa\in[1,2]$ and the loss function is Lipschitz and smooth over a sufficiently large region, we provide a new algorithm based on variance reduced gradient descent that achieves the rate $\tilde{O}\big(\big(\frac{\sqrt{d}}{n\sqrt{\rho}}\big)^\kappa\big)$ on the excess empirical risk, where $n$ is the dataset size and $d$ is the dimension. We further show that this rate is nearly optimal. When $\kappa \geq 2$ and the loss is instead Lipschitz and weakly convex, we show it is possible to achieve the rate $\tilde{O}\big(\big(\frac{\sqrt{d}}{n\sqrt{\rho}}\big)^\kappa\big)$ with a private implementation of the proximal point method. When the KL parameters are unknown, we provide a novel modification and analysis of the noisy gradient descent algorithm and show that this algorithm achieves a rate of $\tilde{O}\big(\big(\frac{\sqrt{d}}{n\sqrt{\rho}}\big)^{\frac{2\kappa}{4-\kappa}}\big)$ adaptively, which is nearly optimal when $\kappa = 2$. We further show that, without assuming the KL condition, the same gradient descent algorithm can achieve fast convergence to a stationary point when the gradient stays sufficiently large during the run of the algorithm. Specifically, we show that this algorithm can approximate stationary points of Lipschitz, smooth (and possibly nonconvex) objectives with rate as fast as $\tilde{O}\big(\frac{\sqrt{d}}{n\sqrt{\rho}}\big)$ and never worse than $\tilde{O}\big(\big(\frac{\sqrt{d}}{n\sqrt{\rho}}\big)^{1/2}\big)$. The latter rate matches the best known rate for methods that do not rely on variance reduction.

From Adaptive Query Release to Machine Unlearning

We formalize the problem of machine unlearning as design of efficient unlearning algorithms corresponding to learning algorithms which perform a selection of adaptive queries from structured query classes. We give efficient unlearning algorithms for linear and prefix-sum query classes. As applications, we show that unlearning in many problems, in particular, stochastic convex optimization (SCO), can be reduced to the above, yielding improved guarantees for the problem. In particular, for smooth Lipschitz losses and any $\rho>0$, our results yield an unlearning algorithm with excess population risk of $\tilde O\big(\frac{1}{\sqrt{n}}+\frac{\sqrt{d}}{n\rho}\big)$ with unlearning query (gradient) complexity $\tilde O(\rho \cdot \text{Retraining Complexity})$, where $d$ is the model dimensionality and $n$ is the initial number of samples. For non-smooth Lipschitz losses, we give an unlearning algorithm with excess population risk $\tilde O\big(\frac{1}{\sqrt{n}}+\big(\frac{\sqrt{d}}{n\rho}\big)^{1/2}\big)$ with the same unlearning query (gradient) complexity. Furthermore, in the special case of Generalized Linear Models (GLMs), such as those in linear and logistic regression, we get dimension-independent rates of $\tilde O\big(\frac{1}{\sqrt{n}} +\frac{1}{(n\rho)^{2/3}}\big)$ and $\tilde O\big(\frac{1}{\sqrt{n}} +\frac{1}{(n\rho)^{1/3}}\big)$ for smooth Lipschitz and non-smooth Lipschitz losses respectively. Finally, we give generalizations of the above from one unlearning request to \textit{dynamic} streams consisting of insertions and deletions.

Private Federated Learning with Autotuned Compression

We propose new techniques for reducing communication in private federated learning without the need for setting or tuning compression rates. Our on-the-fly methods automatically adjust the compression rate based on the error induced during training, while maintaining provable privacy guarantees through the use of secure aggregation and differential privacy. Our techniques are provably instance-optimal for mean estimation, meaning that they can adapt to the ``hardness of the problem" with minimal interactivity. We demonstrate the effectiveness of our approach on real-world datasets by achieving favorable compression rates without the need for tuning.

Faster Rates of Convergence to Stationary Points in Differentially Private Optimization

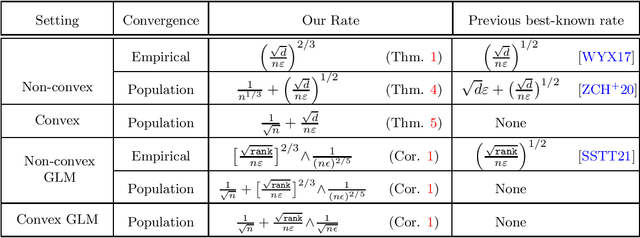
We study the problem of approximating stationary points of Lipschitz and smooth functions under $(\varepsilon,\delta)$-differential privacy (DP) in both the finite-sum and stochastic settings. A point $\widehat{w}$ is called an $\alpha$-stationary point of a function $F:\mathbb{R}^d\rightarrow\mathbb{R}$ if $\|\nabla F(\widehat{w})\|\leq \alpha$. We provide a new efficient algorithm that finds an $\tilde{O}\big(\big[\frac{\sqrt{d}}{n\varepsilon}\big]^{2/3}\big)$-stationary point in the finite-sum setting, where $n$ is the number of samples. This improves on the previous best rate of $\tilde{O}\big(\big[\frac{\sqrt{d}}{n\varepsilon}\big]^{1/2}\big)$. We also give a new construction that improves over the existing rates in the stochastic optimization setting, where the goal is to find approximate stationary points of the population risk. Our construction finds a $\tilde{O}\big(\frac{1}{n^{1/3}} + \big[\frac{\sqrt{d}}{n\varepsilon}\big]^{1/2}\big)$-stationary point of the population risk in time linear in $n$. Furthermore, under the additional assumption of convexity, we completely characterize the sample complexity of finding stationary points of the population risk (up to polylog factors) and show that the optimal rate on population stationarity is $\tilde \Theta\big(\frac{1}{\sqrt{n}}+\frac{\sqrt{d}}{n\varepsilon}\big)$. Finally, we show that our methods can be used to provide dimension-independent rates of $O\big(\frac{1}{\sqrt{n}}+\min\big(\big[\frac{\sqrt{rank}}{n\varepsilon}\big]^{2/3},\frac{1}{(n\varepsilon)^{2/5}}\big)\big)$ on population stationarity for Generalized Linear Models (GLM), where $rank$ is the rank of the design matrix, which improves upon the previous best known rate.

Differentially Private Generalized Linear Models Revisited

We study the problem of $(\epsilon,\delta)$-differentially private learning of linear predictors with convex losses. We provide results for two subclasses of loss functions. The first case is when the loss is smooth and non-negative but not necessarily Lipschitz (such as the squared loss). For this case, we establish an upper bound on the excess population risk of $\tilde{O}\left(\frac{\Vert w^*\Vert}{\sqrt{n}} + \min\left\{\frac{\Vert w^* \Vert^2}{(n\epsilon)^{2/3}},\frac{\sqrt{d}\Vert w^*\Vert^2}{n\epsilon}\right\}\right)$, where $n$ is the number of samples, $d$ is the dimension of the problem, and $w^*$ is the minimizer of the population risk. Apart from the dependence on $\Vert w^\ast\Vert$, our bound is essentially tight in all parameters. In particular, we show a lower bound of $\tilde{\Omega}\left(\frac{1}{\sqrt{n}} + {\min\left\{\frac{\Vert w^*\Vert^{4/3}}{(n\epsilon)^{2/3}}, \frac{\sqrt{d}\Vert w^*\Vert}{n\epsilon}\right\}}\right)$. We also revisit the previously studied case of Lipschitz losses [SSTT20]. For this case, we close the gap in the existing work and show that the optimal rate is (up to log factors) $\Theta\left(\frac{\Vert w^*\Vert}{\sqrt{n}} + \min\left\{\frac{\Vert w^*\Vert}{\sqrt{n\epsilon}},\frac{\sqrt{\text{rank}}\Vert w^*\Vert}{n\epsilon}\right\}\right)$, where $\text{rank}$ is the rank of the design matrix. This improves over existing work in the high privacy regime. Finally, our algorithms involve a private model selection approach that we develop to enable attaining the stated rates without a-priori knowledge of $\Vert w^*\Vert$.

Machine Unlearning via Algorithmic Stability

We study the problem of machine unlearning and identify a notion of algorithmic stability, Total Variation (TV) stability, which we argue, is suitable for the goal of exact unlearning. For convex risk minimization problems, we design TV-stable algorithms based on noisy Stochastic Gradient Descent (SGD). Our key contribution is the design of corresponding efficient unlearning algorithms, which are based on constructing a (maximal) coupling of Markov chains for the noisy SGD procedure. To understand the trade-offs between accuracy and unlearning efficiency, we give upper and lower bounds on excess empirical and populations risk of TV stable algorithms for convex risk minimization. Our techniques generalize to arbitrary non-convex functions, and our algorithms are differentially private as well.

FetchSGD: Communication-Efficient Federated Learning with Sketching

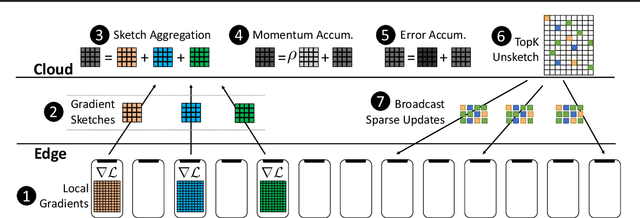
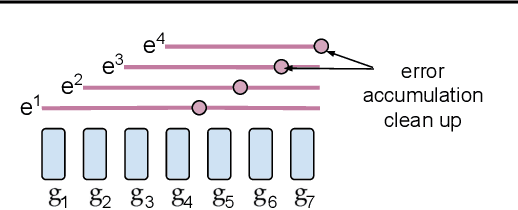
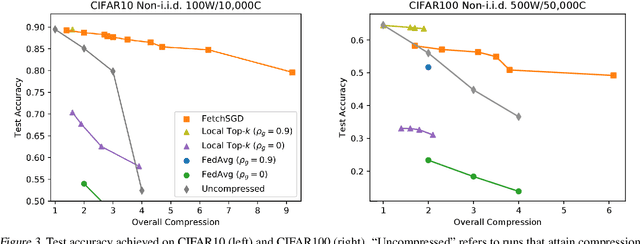
Existing approaches to federated learning suffer from a communication bottleneck as well as convergence issues due to sparse client participation. In this paper we introduce a novel algorithm, called FetchSGD, to overcome these challenges. FetchSGD compresses model updates using a Count Sketch, and then takes advantage of the mergeability of sketches to combine model updates from many workers. A key insight in the design of FetchSGD is that, because the Count Sketch is linear, momentum and error accumulation can both be carried out within the sketch. This allows the algorithm to move momentum and error accumulation from clients to the central aggregator, overcoming the challenges of sparse client participation while still achieving high compression rates and good convergence. We prove that FetchSGD has favorable convergence guarantees, and we demonstrate its empirical effectiveness by training two residual networks and a transformer model.

Private Stochastic Convex Optimization: Efficient Algorithms for Non-smooth Objectives

In this paper, we revisit the problem of private stochastic convex optimization. We propose an algorithm, based on noisy mirror descent, which achieves optimal rates up to a logarithmic factor, both in terms of statistical complexity and number of queries to a first-order stochastic oracle. Unlike prior work, we do not require Lipschitz continuity of stochastic gradients to achieve optimal rates. Our algorithm generalizes beyond the Euclidean setting and yields anytime utility and privacy guarantees.

Communication-efficient distributed SGD with Sketching

Large-scale distributed training of neural networks is often limited by network bandwidth, wherein the communication time overwhelms the local computation time. Motivated by the success of sketching methods in sub-linear/streaming algorithms, we propose a sketching-based approach to minimize the communication costs between nodes without losing accuracy. In our proposed method, workers in a distributed, synchronous training setting send sketches of their gradient vectors to the parameter server instead of the full gradient vector. Leveraging the theoretical properties of sketches, we show that this method recovers the favorable convergence guarantees of single-machine top-$k$ SGD. Furthermore, when applied to a model with $d$ dimensions on $W$ workers, our method requires only $\Theta(kW)$ bytes of communication, compared to $\Omega(dW)$ for vanilla distributed SGD. To validate our method, we run experiments using a residual network trained on the CIFAR-10 dataset. We achieve no drop in validation accuracy with a compression ratio of 4, or about 1 percentage point drop with a compression ratio of 8. We also demonstrate that our method scales to many workers.